私たちは何について話しているのですか

この投稿では、 DVMHコンパイラのランタイムシステム（RTS-以下、ランタイムシステム）の一部について説明します。検討中の部分は、ヘッダーからわかるように、GPUでのユーザー配列の処理、つまり、アクセラレーターメモリでの自動変換または再編成を指します。これらの変換は、計算サイクルでGPUメモリに効果的にアクセスするために行われます。 DVMHとは何か、どのようにコンピューティングに適応できるか、そしてそれが自動的に行われる理由を以下に説明します。

DVMHとは

この投稿は配列変換アルゴリズムのレビューに当てられているため、DVMHが何であるかを簡単に説明します。これは、操作の原理を説明するために必要なためです。 DVM（仮想メモリの分散）システム-ノードのアクセラレーター（GPU NvidiaおよびIntel Xeon Phi）およびマルチコアプロセッサを含むクラスター用のプログラムを開発するように設計されたシステムで開始する必要があります。このシステムを使用すると、主に構造グリッドまたは構造データ型で動作する大規模な順次プログラムを簡単に並列化できるだけでなく、異なるアーキテクチャのデバイスが存在する可能性があるノードにプログラムをクラスターに簡単にマッピングできます。 DVMシステムには以下が含まれます。

Cプログラミング言語（および将来、C ++、もちろん制限付き）およびFortran-C-DVMHおよびFortran-DVMHのコンパイラー。一般的にDVMH言語とコンパイラーを呼び出します。 DVMHは、標準コンパイラーには見えないプラグマまたは特別なコメント（OpenMP、OpenACCなどの類推による）で検討中のプログラミング言語の拡張機能です。したがって、プログラマーは、データがどのように分散され、計算がどのように計算サイクルで分散データにマッピングされるかを示す少数のディレクティブを配置するだけで十分です。その後、ユーザーはシリアルプログラムとパラレルプログラムの両方を受け取ります。結果のプログラムは、異なる数のノード上のクラスター、単一ノード内の1つまたは複数のGPUで実行でき、たとえば、マルチコアプロセッサ、グラフィックアクセラレータ、およびIntel Xeon Phiアクセラレータをすぐに使用できます（これが問題のサーバーにある場合）。詳細については、こちらをご覧ください。
Lib-DVMHサポートライブラリまたはRTSHランタイムシステム（Hはヘテロジニアスを表します。多くのコンポーネントの名前のこの文字は、システムがGPUとXeon Phiをサポートするように拡張された後に表示されます）。このシステムの助けを借りて、プログラムの動作中にユーザープログラムの設定全体が実行されます。
DVMHプログラムの有効性のためのデバッグツールとデバッグツール（これまではFortran-DVMHプログラムのみ）。

このようなシステムを作成する主な目的は、既存のプログラムを並列化することでユーザーの生活を簡素化し、新しい並列プログラムの作成を簡素化することです。 DVMHコンパイラーは、MPI、OpenMP、CUDA、RTSH呼び出しを使用して、DVMHディレクティブを含む結果のプログラムをプログラムに変換します。したがって、ユーザープログラムは、計算配布ディレクティブ（OpenMPまたはOpenACCとほぼ同様）とデータ配布ディレクティブを使用して簡単に並列化できます。さらに、このプログラムは引き続き一貫しており、これはその開発とサポートにとって重要です。それでも、「良い」シーケンシャルプログラムを記述し、DVMHコンパイラ用のそのようなプログラムにディレクティブを配置することは、手動の並列化を行うより簡単です。

同時実行レベル

短い紹介と一連の事柄の紹介の後、初期プログラム（つまり、計算サイクル）がRTSH内の異なるレベルの並列処理にどのようにマッピングされるかを検討します。現在、優れた計算能力を実現するために、各スレッドの頻度を増やす代わりに、単一のデバイス内で多数のスレッドを使用しています。これは、ノード間のプロセスの相互作用の標準（もちろんMPI）だけでなく、異種アーキテクチャの出現、およびさまざまな並列言語（高低両方）の出現も研究する必要につながります。そして、このすべてがエンドユーザーの生活を難しくしています。また、高性能アプリケーションを実現するには、特定のコンピューティングクラスターのすべての機能を使用する必要があります。

現時点では、ノード間とノード内の2つのレベルの並列処理を想像できます。ノード内では、1つ以上のGPUとマルチコアプロセッサを使用できます。このスキームのIntel Xeon Phiは、マルチコアプロセッサを含む別のノードと見なされます。以下は、DVMHプログラムをマッピングできるコンピューティングクラスターの一般的な図です。

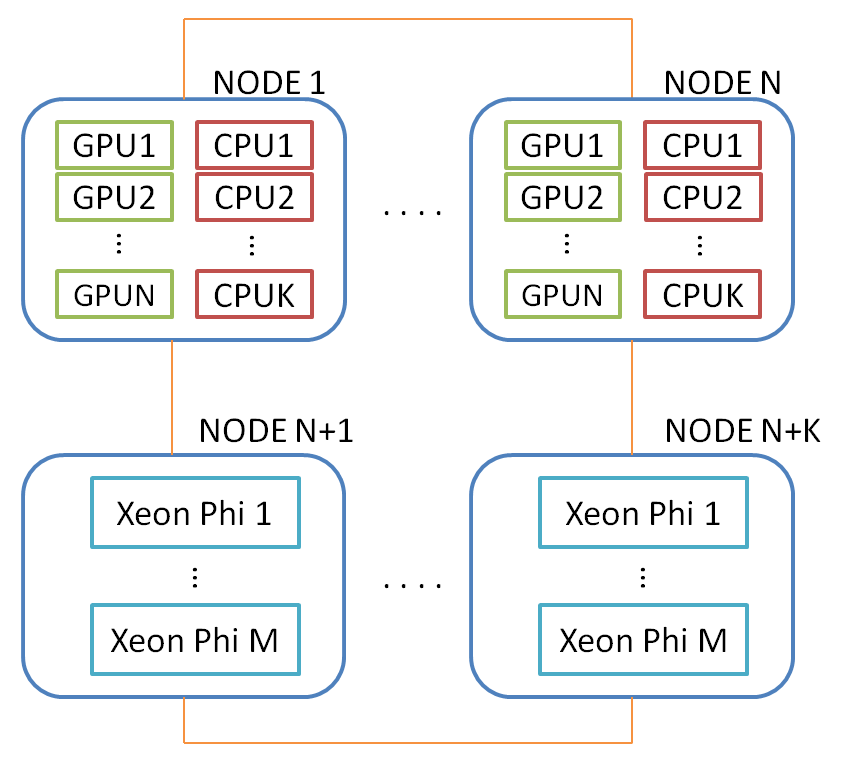
当然、デバイスの負荷を分散する問題（DVMHのメカニズム）が発生しますが、これはこの記事の範囲外です。今後の考慮事項はすべて、単一ノード内の単一GPUに影響します。以下で説明する変換は、DVMHプログラムが独立して動作するすべてのGPUで実行されます。

データの再編成が必要な理由

最後に、長期にわたる紹介の後、再編成の問題自体に取り組みました。なぜこれがすべて必要なのですか？しかし、何のために。ある種の計算サイクルを考えます：

double ARRAY[Z][Y][X][5]; for(int I = 1; i < Z; ++I) for(int J = 1; J < Y; ++J) for(int K = 1; K < X; ++K) ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);

たとえば、最初の（最速の）測定には5つの物理量が含まれ、残りは計算ドメインの空間の座標である4次元配列があります。プログラムでは、最初の（メモリ内に近い）測定がこれら5つの要素で構成されるように配列が宣言されているため、プロセッサキャッシュは計算サイクルで適切に機能します。この例では、3サイクルの各反復で、高速測定の2、4、および5要素へのアクセスが必要です。また、この次元にはサイクルがないことに注意する価値があります。また、たとえば、これらの量の性質が異なるため、5つの要素それぞれの計算も異なります。

したがって、I、J、Kに沿ってループを並列に実行することができますこの例では、ARRAY配列の各要素は、たとえば次のように並列ループにマッピングされます。

 #pragma dvm array distribute[block][block][block][*] double ARRAY[Z][Y][X][5]; #pragma dvm parallel([I][J][K] on ARRAY[I][J][K][*]) for(int I = 1; i < Z; ++I) for(int J = 1; J < Y; ++J) for(int K = 1; K < X; ++K) ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);

つまり、計算が分散されるデータ分布が表示されます。上記のDVMHディレクティブは、配列を等しいブロックで3次元に分散し、4番目（最速）のブロックを乗算する必要があることを示しています。このエントリを使用すると、DVMHプログラムの起動時に指定されたプロセッサラティスにアレイをマッピングできます。次のディレクティブは、ARRAY配列の分散規則に従ってターン（I、J、K）を実行する必要があることを示しています。したがって、PARALLELディレクティブは、ループ反復のマッピングを配列要素に設定します。 RTSHは、実行時に、配列の配置方法と計算の編成方法を認識しています。

このループ、つまりターンの全スペースは、OpenMPスレッドとCUDAスレッドの両方で表示できます。これは、3つのサイクルすべてに依存関係がないためです。 CUDAアーキテクチャへのマッピングに興味があります。 CUDAブロックには3つの次元（x、y、z）が含まれていることは誰もが知っています。最初が最速です。 CUDAブロックのワープにクイック測定が表示されます。なぜこれらすべてを言及する必要があるのですか？次に、グローバルメモリGPU（GDDR5）があらゆるコンピューティングのボトルネックであることを確認します。また、メモリは、ロードされたすべての要素が連続している場合にのみ、1つのワープによって最速のアクセスが提供されるように配置されます。上記のループでは、コイルスペース（I、J、K）をCUDAブロック（x、y、z）にマッピングするための6つのオプションがありますが、ARRAY配列に効率的にアクセスできるオプションはありません。

これは何から来たのですか？配列の説明を見ると、最初の次元に5つの要素が含まれており、サイクルが存在しないことがわかります。したがって、2番目の高速測定の要素は40バイト（double型の5要素）の距離にあり、GPUメモリへのトランザクション数が増加します（1トランザクションではなく、1ワープで最大32トランザクション）。これはすべて、メモリバスの過負荷とパフォーマンスの低下につながります。

この場合、問題を解決するには、1次元と2次元を入れ替える、つまり、2次元行列をX * 5 Y * Z回転置するか、Y * Z独立転置を実行するだけで十分です。しかし、配列の次元を入れ替えるとはどういう意味ですか？次の問題が発生する可能性があります。

この変換を実行するコードにサイクルを追加する必要があります。
プログラムコード内の測定値を再配置する場合、プログラム全体の修正が必要になります。プログラムの1点で配列測定値を再配置すると、すべてのサイクルの計算が不正確になるためです。プログラムが大きい場合、多くの間違いを犯す可能性があります。
順列の効果がどのように得られ、順列が別のサイクルにどのように影響するかは明らかではありません。配列を元の状態に戻す、または配列を戻す必要があります。
このサイクルはCPU上で効率的に実行されなくなるため、プログラムの2つのバージョンを作成します。

RTSHでのさまざまな順列の実装

前述の問題を解決するために、RTSHは配列の自動変換メカニズムを発明しました。これにより、GPUメモリへのアクセスが失敗した場合（この機能を使用しない場合の実行と比較して）、ユーザーのDVMHプログラムを大幅に高速化できます（数回）。変換のタイプとCUDAでの実装を検討する前に、このアプローチの議論の余地のない利点をいくつか挙げます。

ユーザーにはDVMHプログラムが1つあり、アルゴリズムの作成に焦点を当てています。
-autoTfmコンパイラにDVMHオプションを1つだけ指定することにより、DVMHプログラムのコンパイル中にこのモードを有効にできます。したがって、プログラムを変更せずにユーザーは両方のモードを試して、加速を評価できます。
この変換はオンデマンドで実行されます。これは、計算サイクルの前に配列の測定順序が変更された場合、次のサイクルでこの配列の配置が有利になる可能性があるため、計算後の逆置換は実行されないことを意味します。
このオプションを使用せずに実行された同じプログラムと比較して、プログラムの大幅な加速（最大6倍）。

1.物理的に隣接するアレイの次元を交換します。

上記の例は、このタイプの変換に適しています。この場合、2次元平面を転置する必要があります。これは、配列の2つの隣接する次元に配置できます。最初の2次元を転置する必要がある場合は、共有メモリを使用したよく説明されている行列転置アルゴリズムが適切です。

 __shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1]; CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x; CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y; CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x; CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y; CudaSizeType zIndex = blockIdx.z + pZ; CudaSizeType zAdd = zIndex * dimX * dimY; CudaSizeType idx1 = x1Index + y1Index * dimX + zAdd; CudaSizeType idx2 = x2Index + y2Index * dimY + zAdd; if ((x1Index < dimX) && (y1Index < dimY)) { temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1]; } __syncthreads(); if ((x2Index < dimY) && (y2Index < dimX)) { outputMatrix[idx2] = temp[threadIdx.x][threadIdx.y]; }

正方行列の場合、いわゆる「インプレース」を転置することができ、GPUに追加のメモリを割り当てる必要はありません。

2.物理的に隣接していないアレイの次元を交換します。

このタイプには、配列の任意の2次元の順列が含まれます。そのような置換の2つのタイプを強調する価値があります。1つ目は、最初の次元を変更し、それらの間で次元を変更することです。最速の測定の要素は連続しており、それらへのアクセスも連続して可能である必要があるため、この分離は理解できるはずです。これには共有メモリを使用できます。

 __shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1]; CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x; CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y; CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x; CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y; CudaSizeType zIndex = blockIdx.z + pZ; CudaSizeType zAdd = zIndex * dimX * dimB * dimY; CudaSizeType idx1 = x1Index + y1Index * dimX * dimB + zAdd; CudaSizeType idx2 = x2Index + y2Index * dimY * dimB + zAdd; for (CudaSizeType k = 0; k < dimB; k++) { if (k > 0) __syncthreads(); if ((x1Index < dimX) && (y1Index < dimY)) { temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1 + k * dimX]; } __syncthreads(); if ((x2Index < dimY) && (y2Index < dimX)) { outputMatrix[idx2 + k * dimY] = temp[threadIdx.x][threadIdx.y]; } }

他の測定値を相互に再配置する必要がある場合、共有メモリは必要ありません。アレイの高速測定へのアクセスが「正しく」実行されるためです（隣接するスレッドはGPUメモリ内の隣接セルで動作します）。

3.配列を対角化します。

このタイプの順列は非標準であり、通常のデータ依存性を持つサイクルの並列実行に必要です。この順列は、依存関係があるサイクルを処理するときに「正しい」アクセスを提供します。そのようなループの例を考えてみましょう。

 #pragma dvm parallel([ii][j][i] on A[i][j][ii]) across(A[1:1][1:1][1:1]) for (ii = 1; ii < K - 1; ii++) for (j = 1; j < M - 1; j++) for (i = 1; i < N - 1; i++) A[i][j][ii] = A[i + 1][j][ii] + A[i][j + 1][ii] + A[i][j][ii + 1] + A[i - 1][j][ii] + A[i][j - 1][ii] + A[i][j][ii - 1];

この場合、サイクルの3次元すべてまたは配列Aの3次元に依存しています。DVMHコンパイラに、このサイクルに通常の依存があることを通知するために（依存要素は式a * x + bで表現できます。aおよびbは定数）、ACROSS仕様が存在します。このサイクルには、直接および逆の依存関係があります。このサイクルのターンの空間は、平行六面体（および特定の場合-三次元立方体）によって形成されます。各面に対して45度回転したこの平行六面体の面は、面自体が直列になっている間、並行して実行できます。このため、配列Aの最初の2つの最速測定の対角要素へのアクセスが表示されますGPUのパフォーマンスを向上させるには、配列の対角変換を実行する必要があります。単純な場合、1つの平面の変換は次のようになります。

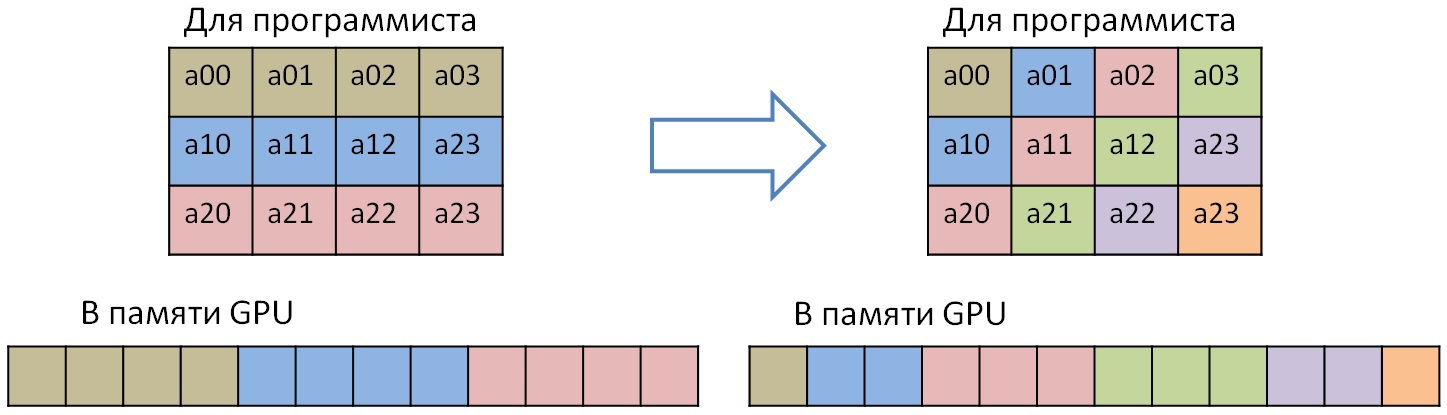
この変換は、行列を転置するのと同じ速さで実行できます。これを行うには、共有メモリを使用します。行列の転置とのみ対照的に、処理されるブロックは正方形ではなく、平行四辺形の形であるため、読み取りおよび書き込み時にGPUメモリ帯域幅を使用するのが効率的です（他のすべてが同じように壊れているため、最初のストリップのみが対角化のために示されています）：

次のタイプの対角化が実装されています（RxおよびRyは、対角化された長方形のサイズです）。

側面の対角線に平行で、Rx == Ry;
側面の対角線に平行で、Rx <Ry;
側面の対角線に平行で、Rx> Ry;
主対角線に平行で、Rx == Ry;
主対角線に平行で、Rx <Ry;
主対角線およびRx> Ryに平行。

対角化の一般的なコアは次のとおりです。

 __shared__ T data[BLOCK_DIM][BLOCK_DIM + 1]; __shared__ IndexType sharedIdx[BLOCK_DIM][BLOCK_DIM + 1]; __shared__ bool conditions[BLOCK_DIM][BLOCK_DIM + 1]; bool condition; IndexType shift; int revX, revY; if (slash == 0) { shift = -threadIdx.y; revX = BLOCK_DIM - 1 - threadIdx.x; revY = BLOCK_DIM - 1 - threadIdx.y; } else { shift = threadIdx.y - BLOCK_DIM; revX = threadIdx.x; revY = threadIdx.y; } IndexType x = (IndexType)blockIdx.x * blockDim.x + threadIdx.x + shift; IndexType y = (IndexType)blockIdx.y * blockDim.y + threadIdx.y; IndexType z = (IndexType)blockIdx.z * blockDim.z + threadIdx.z; dvmh_convert_XY<IndexType, slash, cmp_X_Y>(x, y, Rx, Ry, sharedIdx[threadIdx.y][threadIdx.x]); condition = (0 <= x && 0 <= y && x < Rx && y < Ry); conditions[threadIdx.y][threadIdx.x] = condition; if (back == 1) __syncthreads(); #pragma unroll for (int zz = z; zz < z + manyZ; ++zz) { IndexType normIdx = x + Rx * (y + Ry * zz); if (back == 0) { if (condition && zz < Rz) data[threadIdx.y][threadIdx.x] = src[normIdx]; __syncthreads(); if (conditions[revX][revY] && zz < Rz) dst[sharedIdx[revX][revY] + zz * Rx * Ry] = data[revX][revY]; } else { if (conditions[revX][revY] && zz < Rz) data[revX][revY] = src[sharedIdx[revX][revY] + zz * Rx * Ry]; __syncthreads(); if (condition && zz < Rz) dst[normIdx] = data[threadIdx.y][threadIdx.x]; } }

この場合、dvmh_convert_XYを使用して、条件値と計算された座標をdvmh_convert_XYを使用して他のスレッドに転送する必要があります。転置とは異なり、両方の座標（読み取り場所と書き込み場所）を明確に計算することはできないためです。

結果。実装されている順列：

配列の隣接する2つの次元を再配置します。
隣接しない2つの配列次元の再配置。
隣接する2つの最速の配列次元のダイゴナイゼーション。
[計画済み]配列の任意の2つの最速次元の対角化（対角化可能な次元が最速になります）。
対角化可能な配列からのクリッピングのコピー（たとえば、複数のGPUでカウントする場合に「シャドウ」エッジを更新する）。

性能評価

アプローチの有効性を実証するために、順列自体のパフォーマンスを示すグラフを提供し、2つのプログラムの結果を示します：ガス流体力学問題のLU分解と、3次元ディリクレ問題の解の連続的上部緩和の方法を実装する合成テストです。すべてのテストは、GTX Titan GPUとNvidia CUDA ToolKit 7.0、およびIntelコンパイラバージョン15を搭載したIntel Xeon E5 1660 v2プロセッサで実行されました。

配列の再編成は、特定の規則に従ってメモリの一部を別のメモリにコピーするため、実装されたすべての変換を通常のコピーのコアと比較します。コピーコアは次のようになります。

 __global__ void copyGPU(const double *src, double *dist, unsigned elems) { unsigned idx = blockIdx.x * blockDim.x + threadIdx.x; if(idx < elems) dist[idx] = src[idx]; }

この場合、CUDAブロック内の同期、および共有メモリ（L1キャッシュ）へのアクセスに追加のオーバーヘッドがあり、コピーパフォーマンスが低下するため、共有メモリを使用するアルゴリズムに対してのみ変換速度を指定します。その他の順列。 100％の場合、copyGPUコピーコアの速度を使用します。この場合、オーバーヘッドは最小限であり、このコアにより、ほぼ最大のGPUメモリ帯域幅を取得できます。

最初のグラフは、2次元マトリックスの変換（転置）と対角化がどれほど遅いかを示しています。マトリックスサイズの範囲は、数メガバイトから1ギガバイトです。グラフから、2次元マトリックスでは、copyGPUコアと比較してパフォーマンスが20〜25％低下していることがわかります。対角化アルゴリズムは行列転置よりもやや複雑であるため、対角化が5％長く実行されることもわかります。

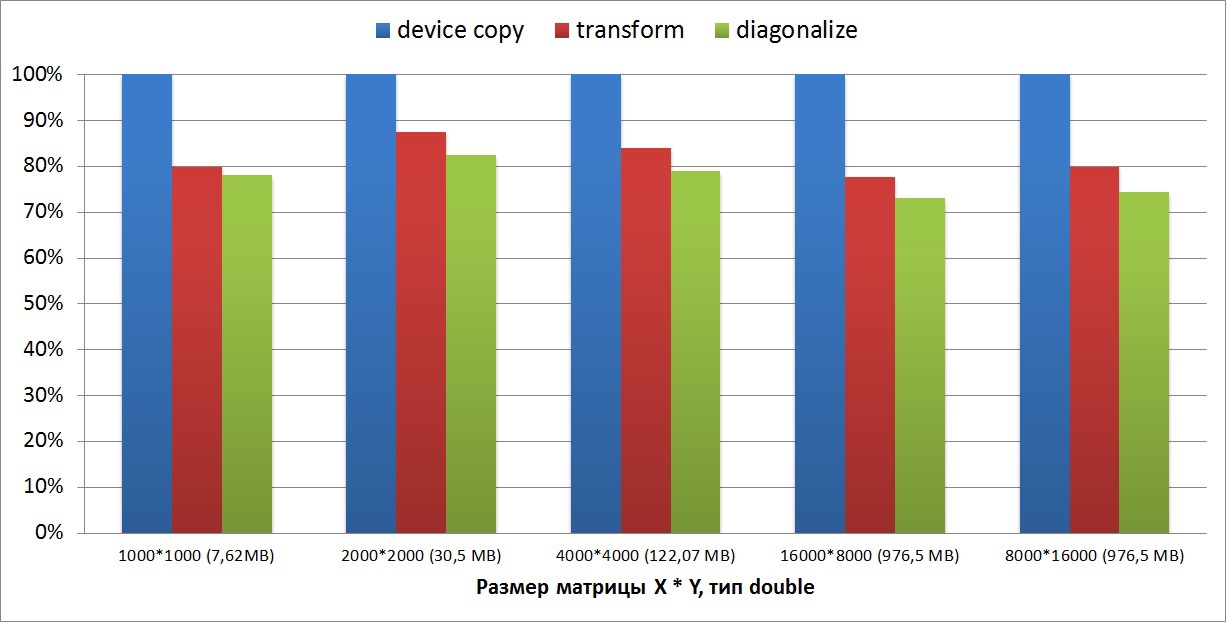
2番目のグラフは、3次元マトリックスの変換（転置）および対角化がどれほど遅いかを示しています。マトリックスのサイズは、4次元のタイプN * N * N * 5と任意のX * Y * Zの2つのタイプで取得されました。マトリックスサイズの範囲は10メガバイトから500メガバイトです。小さなマトリックスでは、変換速度は40％低下しますが、大きなマトリックスでは、変換速度は90％に達し、対角化率はコピー速度の80％です。

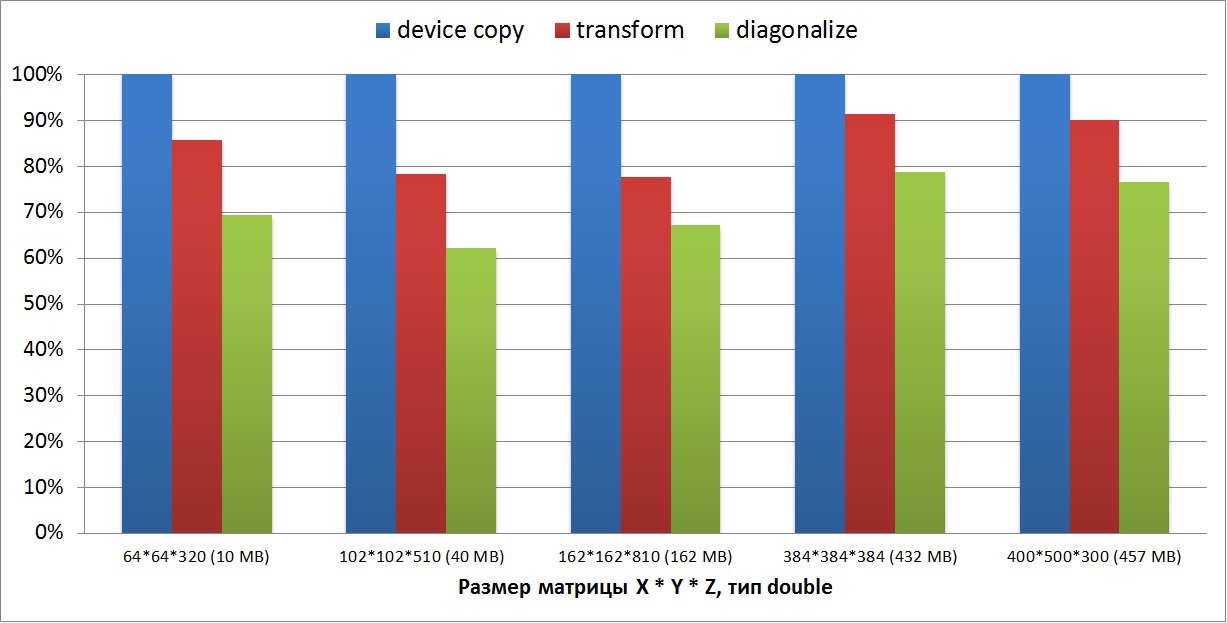
3番目のグラフは、シンセティックテストの実行時間を示しています。これは、対称上部緩和の方法を実装しています。このメソッドの計算サイクルには、3つの次元すべての依存関係が含まれます（Cのこのサイクルについては上記で説明しています）。このグラフは、同じDVMHプログラム（Fortranで記述され、ソースコードは記事の最後に添付されています）の実行時間を示しています。この場合、対角化は、反復計算の前に一度だけ行う必要があります。

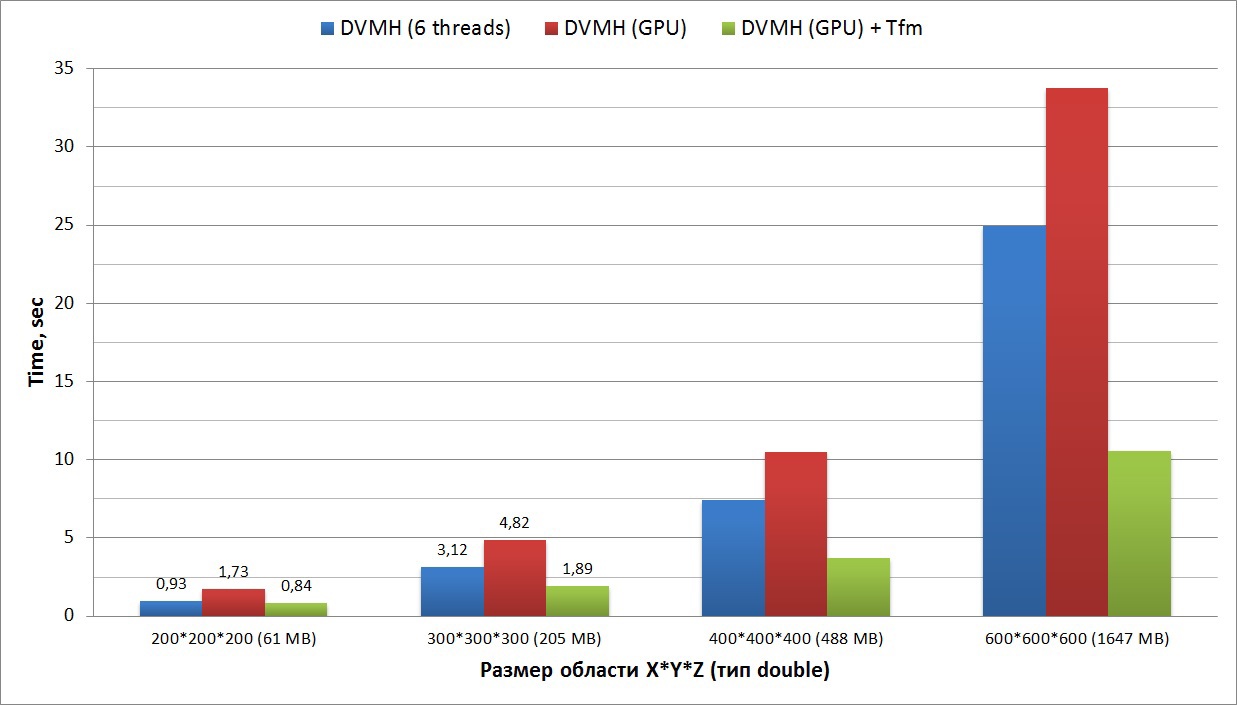
4番目のグラフは、対称逐次上緩和法（SSORアルゴリズム、LU問題）を使用して、非線形偏微分方程式の合成システム（圧縮性液体または気体の方程式の3次元ナビエストークスシステム）を解くアプリケーションの加速を示しています。このテストは、標準のNASAテストスイート（最新バージョン3.3.1）の一部です。このセットでは、MPIとOpenMPだけでなく、シーケンシャルバージョンのすべてのテストのソースコードが利用できます。

このグラフは、Xeon E5の1つのコア、Xeon E5の6つのスレッド、および2つのモードのGPUで実行されるシリアルバージョンに対するプログラムの加速を示しています。このプログラムでは、2サイクルだけ対角化を行い、配列を元の状態に戻す必要があります。つまり、「不良」サイクルの各反復で、必要なすべての配列が対角化され、実行後に対角化が行われます。このプログラムには、Fortran 90スタイルの約25万行があることに注意してください（ハイフネーションなしで、コードは記事の最後に添付されます）。 125個のDVMHディレクティブを追加して、このプログラムをクラスター上、異なるデバイス上の1つのノード上、およびシリアルモードで実行できるようにしました。

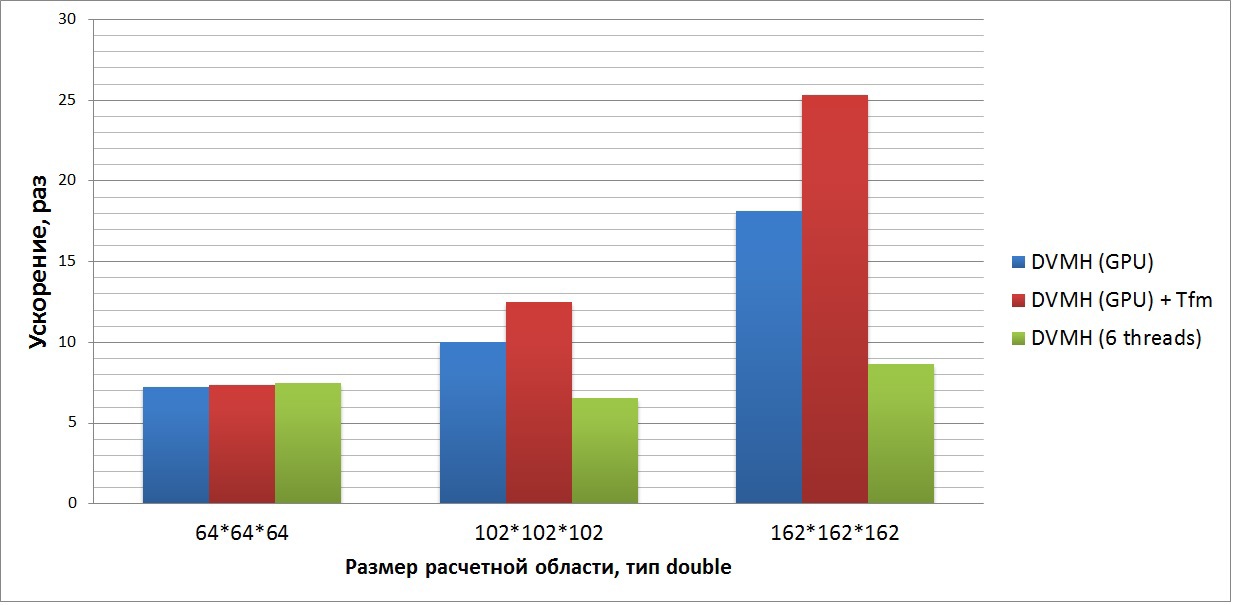
このプログラムは、シリアルコードのレベルで最適化されており（6 Xeon E5コアの8倍の高速化からわかる）、GPUアーキテクチャだけでなくマルチコアプロセッサでも適切に表示されます。 DVMHコンパイラでは、-Minfoオプションを使用して、表示された各サイクルに対応するCUDAカーネルに必要なレジスタの数を確認できます（この情報はNvidiaコンパイラから取得されます）。この場合、3つのメインコンピューティングサイクルのそれぞれに、スレッドあたり約160個のレジスタ（255個のうち使用可能）が必要であり、グローバルメモリにアクセスする操作の数は約10：1です。したがって、再編成の使用による加速はそれほど大きくありませんが、それはまだ存在し、大きなタスクの場合、このオプションなしで実行された同じプログラムと比較して1.5倍です。また、このテストは、6つのCPUコアよりもGPUで3倍高速に実行されます。

おわりに

この投稿では、DVMHプログラムを実行するためのサポートシステムで、GPU上のデータを自動的に再編成する方法が検討されました。この場合、このプロセスの完全な自動化について話しています。 RTSHには、再編成のタイプを判別するために必要なプログラムの実行中にすべての情報が含まれています。このアプローチにより、GPUグローバルメモリが最適な方法でアクセスされたサイクルを表示するときに、「適切な」シーケンシャルプログラムを作成できないプログラムで適切な加速を実現できます。変換を実行すると、デバイス内の最速のメモリコピーコアと比較して、グローバルGPUメモリ（GTX Titanの場合は約240 GB / s）のパフォーマンスの最大90％が達成されます。

参照資料

1） DVMシステム

2） Fotran-DVMHのソースコードLUおよびSOR

3） NASAテスト

グラフィックスアクセラレータのメモリ内の配列の自動再編成