

実際には、タスクはフィールドのすべてのセルを「オフ」にすることです。 katomの下では、単なる解決策よりも興味深いものがあります。
解決アルゴリズム自体はかなり面倒であり、説明に長い時間がかかります。 要するに、各サイズのフィールドには、すべての可能な動きのバイナリ行列Aがあります。 初期フィールドをバイナリベクトルXの形式で表す場合、フィールドbの解はバイナリ線形方程式Ab = Xのシステムの解です。マトリックスAを反転し、変数に格納し、式b = Aを使用して任意のフィールドの解を見つけることは簡単です1 X.誰かがもっと読みたいなら、すべてのニュアンスを説明する素晴らしい記事があります。 先に進みます。
ちなみに、ソリューションはどのディメンションにも常に存在するとは限りません。 たとえば、5x5や17x17のサイズには必ずしも解決策があるとは限らず、この記事ではそれらを考慮していません。
パターン生成
たとえば、次の20x20フィールドを考えてみましょう。

次に、彼の解決策を見てみましょう。

いいですね サイズを大きくしてみましょう(そして境界線をオフにします。そうしないと、境界線が目に入ります)。 たとえば、75x75を例にとります。

そして彼の解決策を見てください:

かなりきれい。 しかし、時間を無駄にせずに、すぐに150x150かかります:

そして、彼の決断は...うわー。

魅惑的。 遠くから見ると、それは都市計画のように見えます。 または古代ギリシャのモザイク。 またはトルクメン絨毯の上。 何らかの理由で緑のみ。
そして、解決策の解決策を得ようとするとどうなりますか? 別のパターン、派生物を取得します。 そして、あなたは再びそれをして、別の派生パターンを得ることができます。



この場合、遅かれ早かれ、パターンはループします。 異なるサイズには異なる期間がありますが、偶数フィールドでは期間が奇数フィールドよりも長くなります(6x6および7x7、大きなサイズでは期間はすでに数百の最小値です):


同時に、派生パターンは軸反射対称を保持します(アニメーションはループされません。ループバージョンには2045フレームが必要です)。



反射に加えて、派生パターンは回転対称性を維持することもできます。

ハッシュ
パターンに加えて、Lights Outは、低速で暗号的に不安定な(決定性のため)が、エキゾチックなハッシュ関数として使用できます。
それを数えるには? たとえば、フィールド全体を初期値と見なす場合、2番目の派生フィールドの最初の2列をハッシュとして使用できます。 これらはハッシュ関数のメインタスクを保存します-初期データにわずかな変更を加えるだけで、ハッシュは著しく変化します。 ここで、自分で見てください:

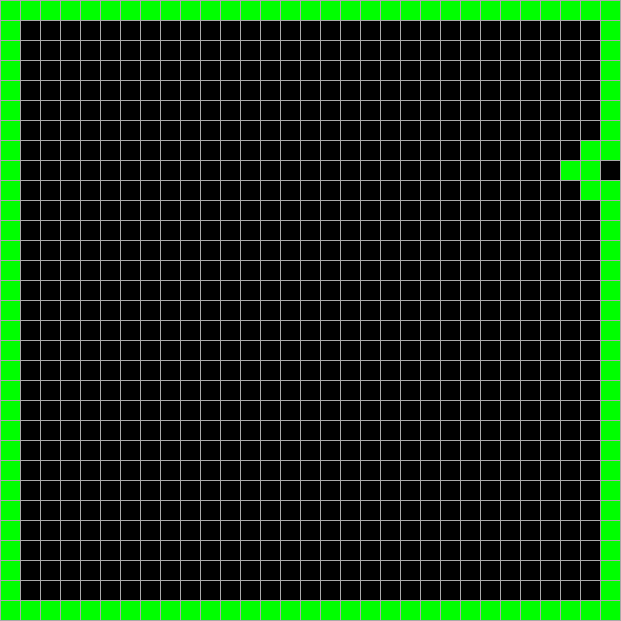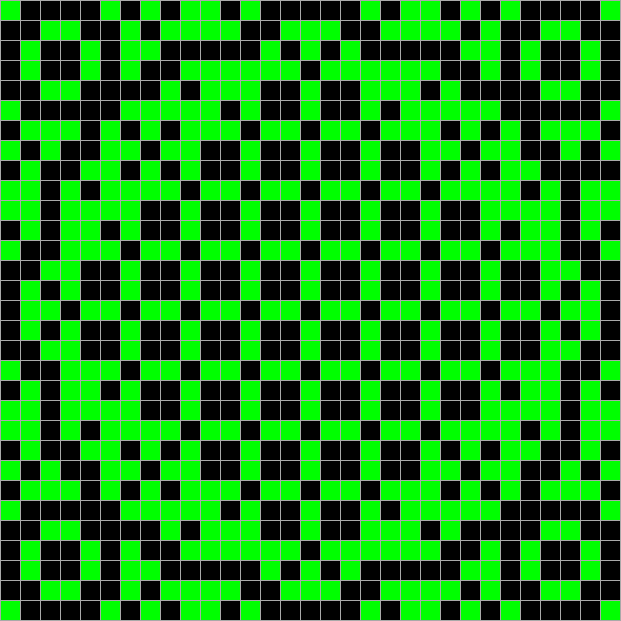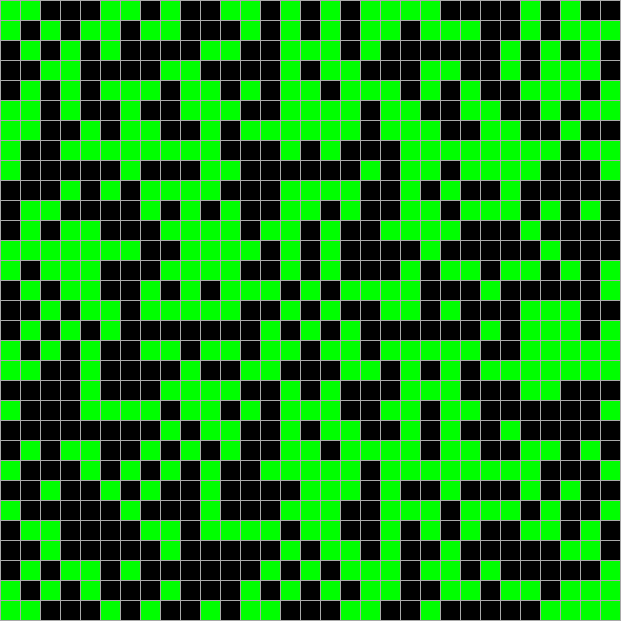
そしてハッシュのみ:


アニメーションなしで、違いに気付くには:


これはどこに適用できますか? まあ、おそらくどこにもありません。 チェックサムには遅すぎます。 このハッシュを与える初期データを選択することは非常に簡単であるため、暗号化にも適用できません。 しかし、珍しい。
データ隠蔽
最後の用途は、フィールド内のデータの非表示です。 フィールドに何かを描いてから、派生パターンを数回計算し、どこかに置くことができます。 そして、周期的な性質のおかげで、最初に暗号化されたフィールドは遅かれ早かれ自分自身を表示します。 次に例を示します(慎重に、252フレームのGIF)。 どちらかといえば、9番目のフレームのデータ:

codeplexにソースコードがあるアプリケーション 。 残念ながら、Windows専用のバージョンがあります。