タスクの条件に従って、刑務所には100人の囚人がおり、それぞれが1から100の個人番号を持っています。看守は囚人に釈放の機会を与え、彼が発明したテストに合格することを申し出ます。 すべての囚人が成功すれば、彼らは自由です; 1人でも失敗すれば、誰もが死にます。

挑戦する
看守は秘密の部屋に入り、蓋付きの100箱を準備します。 彼は各箱に1から100までの数字を付けます。次に、囚人の数に応じて100枚の紙皿を持ち、これらの板に1から100までの番号を付けます。 。 囚人は、看守がこれらのすべての行動をどのように実行するかを見ていません。

競技が始まると、看守は各囚人を1つずつ箱入りの部屋に連れて行き、囚人にナンバープレートが置かれる箱を見つけなければならないことを伝えます。 囚人は、箱を開けて自分の番号のついた皿を見つけようとします。 それぞれ50個までのボックスを開くことができます。 各囚人が自分の番号を見つけた場合、囚人は解放されます。少なくとも1人が50回の試行で自分の番号を見つけられなかった場合、すべての囚人が死にます。

囚人が釈放されるためには、すべての囚人が試験に合格しなければなりません。
それで、囚人が慈悲を持つチャンスは何ですか?
- 囚人が箱を開けてプレートをチェックした後、箱に戻して蓋を再び閉じます。
- プレートは交換できません。
- 囚人は、テストの開始後、お互いに手がかりを与えたり、何らかの形で相互作用したりすることはできません。
- 囚人は、テストの前に戦略について話し合うことができます。
囚人にとって最善の戦略は何ですか?
追加の質問:
テストの開始前に仲間の囚人(テスト参加者ではない)が秘密の部屋に入ることができる場合、すべての箱のすべてのプレートを調べ、(オプションで、必ずしもそうではないが)2つのボックスの2つのプレートを交換します(そして、コンパニオンには機会がありません)囚人に彼らの行動の結果を知らせるために)、それから彼は囚人の救いの機会を増やすためにどんな戦略を取るべきですか?
解決策はないでしょうか?
一見したところ、このタスクはほとんど絶望的です。 各囚人が自分の皿を見つける可能性は顕微鏡的には小さいようです。 さらに、囚人は裁判中に互いに情報を交換することはできません。
1人の囚人の確率は50:50です。 箱は100箱のみで、プレートを探して最大50箱まで開けることができます。 箱をランダムに開き、すべての箱の半分を開くと、箱の開いた半分に自分の皿が見つかるか、閉じた50箱に残ったままになります。 彼の成功の可能性は½です。

2人の囚人を連れて行く。 両方がランダムにボックスを選択した場合、それぞれに対してオッズは½になり、2つの½x1=¼になります。
(2人の囚人の場合、成功は4人に1人になります)。
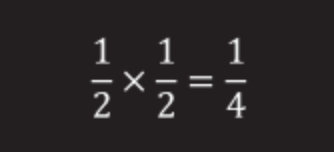
3人の囚人の場合、オッズは½×½×½= beになります。
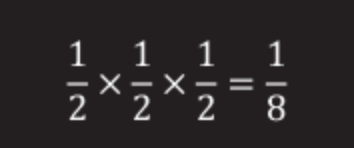
100人の囚人の場合、オッズは次のとおりです。½×½×...½×½(100倍)。
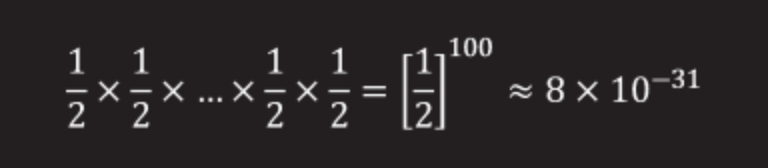
等しい
Pr≈0.0000000000000000000000000000008
つまり、これは非常に小さなチャンスです。 この状況では、ほとんどの場合、すべての囚人が死亡します。
ソリューションをさらに読む前に、これを考慮することをお勧めします。
信じられないほどの答え
各囚人がランダムにボックスを開く場合、テストに合格する可能性は低いです。 囚人が30%以上のケースで成功を期待できる戦略があります。 これは信じられないほど信じられないほどの結果です(以前にこの数学の問題について聞いたことがない場合)。
100人の囚人全員に対して30%以上! はい、これは箱をランダムに開けるという条件で、2人の囚人の可能性以上のものです。 しかし、これはどのように可能ですか?
各囚人の1人が50%を超える可能性はないことは明らかです(結局、囚人間のコミュニケーションの方法はありません)。 ただし、ボックス内のラベルの場所に情報が保存されることを忘れないでください。 個々の囚人への訪問の間にタブレットをシャッフルする人はいないため、この情報を使用できます。
解決策
最初に解決策を説明し、次にそれが機能する理由を説明します。
戦略は非常に簡単です。 最初の囚人は、服に書かれた番号の入った箱を開きます。 たとえば、囚人番号78は、ボックス番号78を開きます。ボックス内のプレートで自分の番号を見つけたら、それは素晴らしいことです。 そうでない場合、彼は自分の箱のプレート上の番号を見て、その番号で次のボックスを開きます。 2番目のボックスを開いた後、彼はこのボックス内のプレート番号を見て、この番号で3番目のボックスを開きます。 次に、この戦略を残りのボックスに転送します。 明確にするために、次の図を見てください。
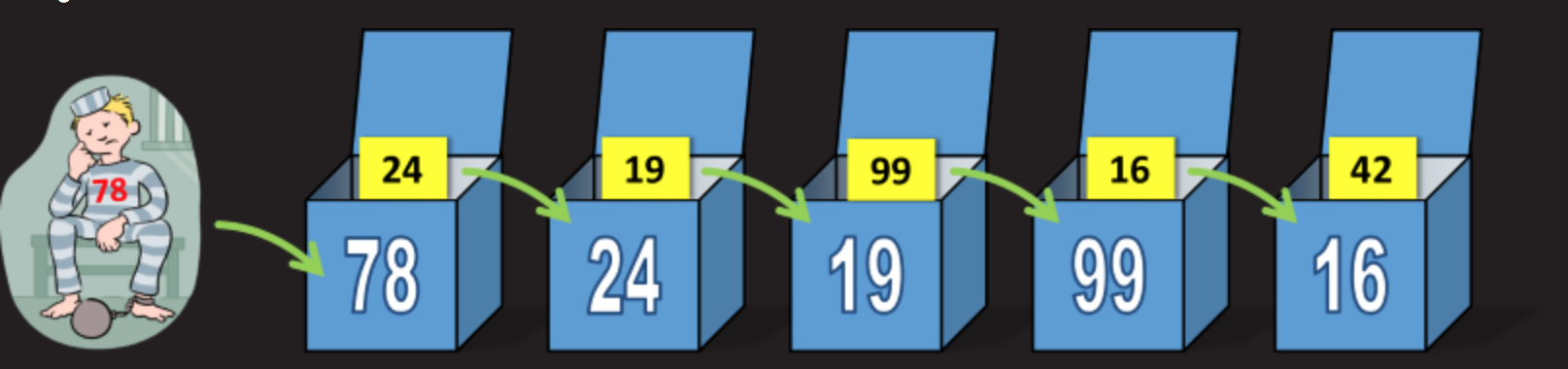
最終的に、囚人は自分の番号を見つけるか、50ボックスの制限に達します。 一見、ランダムにボックスを選択するのと比較して無意味に見えます(そして、1人の囚人にとってはそうです)が、100人の囚人全員が同じボックスのセットを使用するので、理にかなっています。
この数学的問題の美しさは、結果を知るだけでなく、この戦略が機能する理由を理解することでもあります。
では、なぜ戦略が機能するのでしょうか?
各ボックスには1つのプレートがあり、このプレートはユニークです。 これは、ラベルが同じ番号のボックスにあるか、別のボックスを示していることを意味します。 すべてのプレートは一意であるため、それを指すボックスごとに1つのプレートしかありません(このボックスに到達する方法は1つしかありません)。

考えてみると、ボックスは閉じた丸いチェーンを形成しています。 1つのボックスは1つのチェーンのみの一部になります。これは、ボックス内には次へのポインターが1つしかないため、前のボックスにはこのボックスへのポインターが1つしかないためです(プログラマーはリンクリストの類推を見ることができます)。
ボックスがそれ自体を示さない場合(ボックス番号はその中のプレートの番号に等しい)、それはチェーンになります。 チェーンの中には2つのボックスで構成されるものもあれば、長いものもあります。
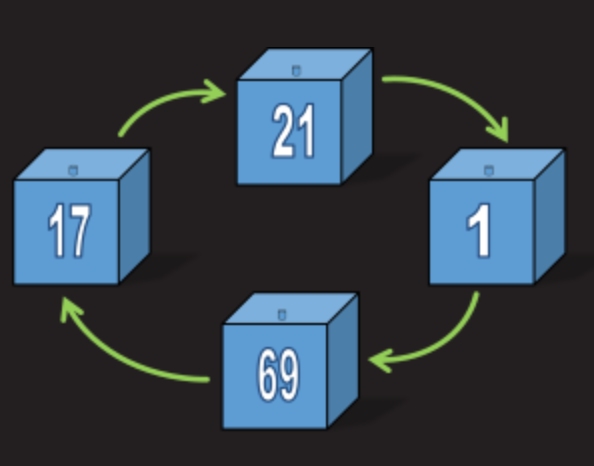
すべての囚人は服と同じ番号の箱から始まるため、定義上、プレートを含むチェーンに乗ります(このボックスを示すプレートは1つだけです)。
このチェーン内のボックスを円で探索すると、最終的にネームプレートを見つけることが保証されます。
残っている唯一の問題は、彼らが50手でタブレットを見つけるかどうかです。
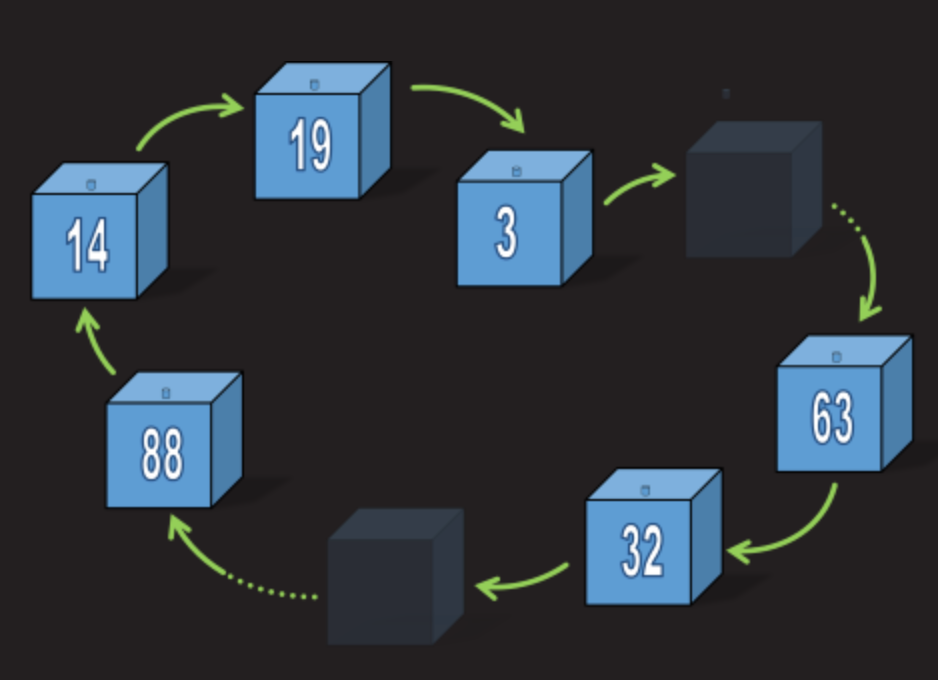
チェーン長
すべての囚人がテストに合格するには、最大チェーン長が50ボックス未満である必要があります。 チェーンが50ボックスよりも長い場合、これらのチェーンの数字を持つ囚人はテストに失敗し、すべての囚人が死亡します。
最長チェーンの最大長が50ボックス未満の場合、すべての囚人がテストに合格します。
少し考えてみてください。 ラベルのレイアウトには50ボックスより長いチェーンが1つしか存在しないことがわかります(100ボックスしかないため、1つのチェーンが50より長い場合、残りは合計で50より短くなります)。

ロングチャンスの機会
成功するためには、最大チェーン長は50以下でなければならず、どのセットにも長いチェーンは1つしか存在できないと確信した後、テストに合格する確率を計算できます。

もう少し数学
それでは、長いチェーンの可能性を把握するには何が必要ですか?
長さがlのチェーンの場合、ボックスがこのチェーンの外側にある確率は次の値に等しくなります。
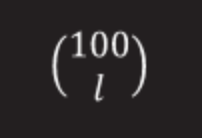
この数字のコレクションには(l-1)があります! プレートを配置する方法。
残りのプレートは配置できます(100-l)! 方法(チェーンの長さが50を超えないことを忘れないでください)。
この場合、正確な長さlのチェーンを含む順列の数:(> 50)

ラベルのレイアウト方法は100(!)あるため、長さlのチェーンの確率は1 / lです。 ところで、この結果はボックスの数に依存しません。
既に知っているように、長さが50を超えるチェーンがあるオプションは1つしか存在しないため、成功の確率は次の式を使用して計算されます。
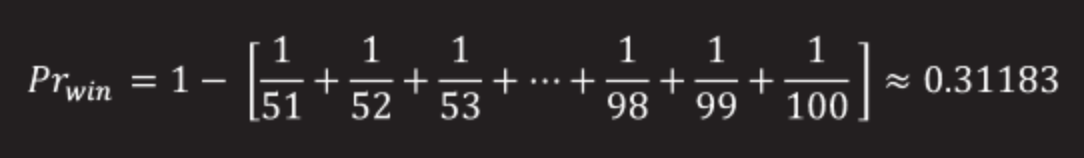
結果
31.18%-最長チェーンのサイズが50未満であり、50回の試行の制限がある場合、各囚人が自分のプレートを見つけることができる可能性。
すべての囚人がタブレットを見つけてテストに合格する可能性31.18%
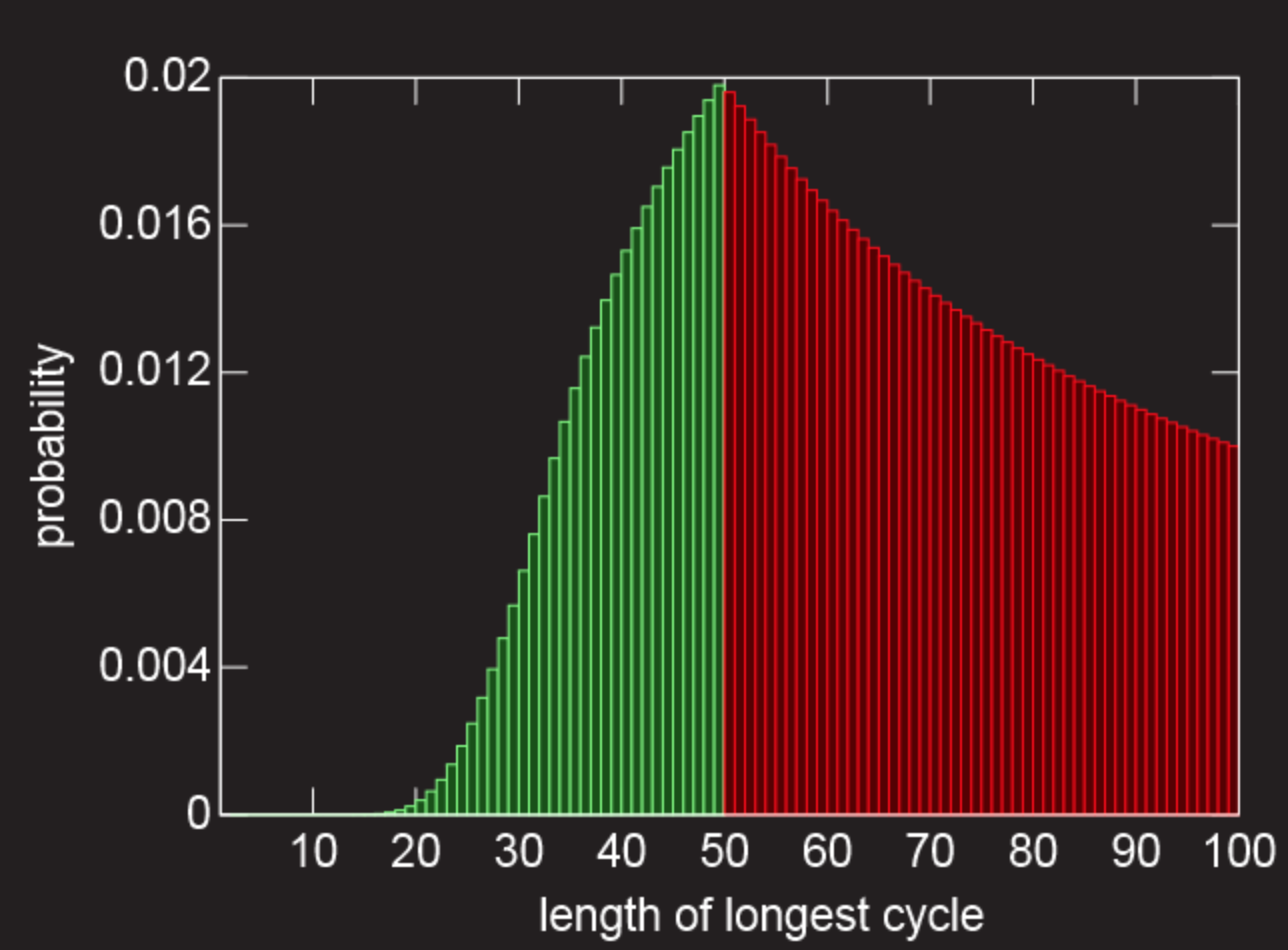
以下は、長さlのすべてのチェーン(横座標)の確率(縦座標に沿って)を示すグラフです。 赤色はすべての「失敗」を意味します(この曲線は1/1グラフです)。 緑色は「成功」を意味します(最大長を決定する方法は50未満であるため、グラフのこの部分の計算はもう少し複雑です)。 緑の列の合計確率は、救いの31.18%の確率です。
調和数(記事のこの部分はオタク向けです)
数学では、n番目の調和数は、自然数列の最初のn個の連続した数の逆数の合計です。

対応する調和数を追加することで、ジェイルブレイクの確率を計算できます。
100aボックスではなく、任意の多数のボックスがある場合、制限を計算します(合計で2n個のボックスがあると仮定しましょう)。
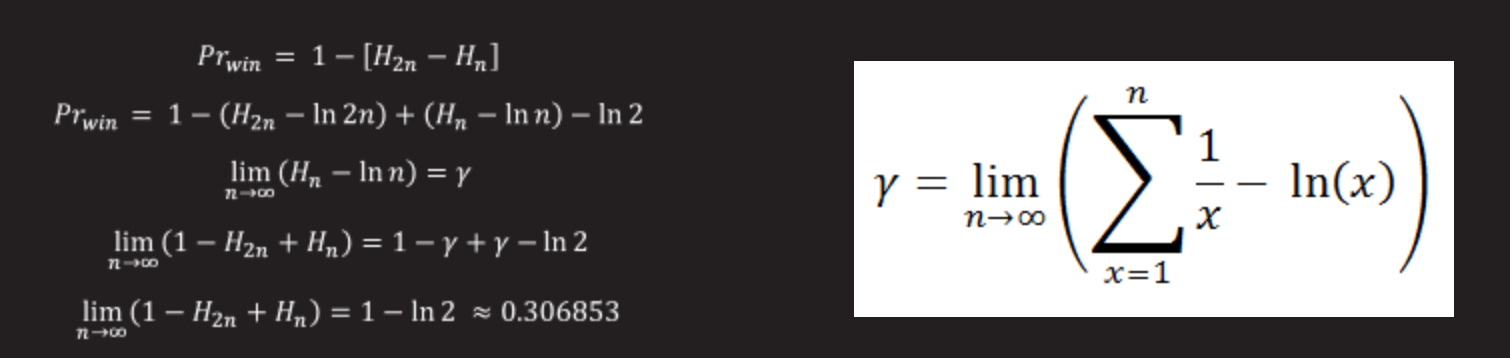
オイラー-マスケローニ定数は、調和級数の部分和と数値の自然対数との差の限界として定義される定数です。
囚人がすべての箱の半分を開くことを監督者が許可する場合、囚人の数が増えると、救われる可能性は30.685%になります。
(囚人が誤って箱を推測するという決定をした場合、囚人の数が増えると、救われる確率はゼロになる傾向があります!)
追加の質問
他の誰かが追加の質問を覚えていますか? 私たちの役に立つ同志は、生存の可能性を高めるために何ができますか?
今、私たちはすでに解決策を知っているので、ここでの戦略は簡単です。彼はすべてのプレートを調べ、ボックスの最も長いチェーンを見つけなければなりません。 最長チェーンが50未満の場合、プレートをまったく変更したり、最長チェーンが50より長くならないようにプレートを変更したりする必要はありません。 ただし、50ボックスより長いチェーンを見つけた場合、このチェーンから2つのボックスの内容を変更して、このチェーンを2つの短いチェーンに分割するだけです。
この戦略の結果、長い鎖はなくなり、すべての囚人はタブレットと救いを見つけることが保証されます。 したがって、2つのプレートを交換することで、救われる確率を100%に減らすことができます!