
自分で組み立てることはできませんでした(常に1つのフラグメントが残っていました)。 したがって、プログラムを作成することが決定されました。
読みたくない人のために、解決策は参照によって利用可能です(注意、それはプロセッサに大きな負荷をかけます)。
したがって、5x5x5の立方体に配置する必要のある25個の同一の要素で構成されるパズルがあり、要素の最小のエッジが測定単位として使用されます。
言語の選択はJavaScriptにかかっていました。 視覚化のためにパフォーマンスを犠牲にしました(映画のように視覚化されたブルートフォースを作りたかったのですが)、検索プロセスの利点は長すぎるとは約束されていませんでした(理由は以下に記述します)。
パズル要素を片面のキューブに分割する 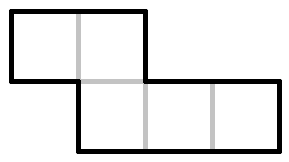

メインアセンブリプロセスは3次元整数配列(5x5x5)で行われます。これを「ボックス」と呼びます。ここでは、要素のキューブが占めるセルを負でない値で示します。 情報量が多い場合、この値は3次元空間での要素の位置のシリアル番号になります。 各軸の周りの回転角が90°の倍数である場合、合計で、3次元空間に要素の24の位置があります。 位置の数を数えやすくするために、
3次元空間でのオブジェクトの位置の数を把握し、各状態の反射で補完する(他の2つの反射は、一緒に、別々に、同じ立方体またはねじれ後の最初の反射のいずれかを与えます)、ユニークなパズルソリューションごとに複数存在することができます、さらに47種類のバリエーションがあり、したがって、ソリューションに必要な時間は徹底的な検索の時間よりも短くなります。 残念ながら、解決策を見つけるために移動回数を計算するための式を推測することはできません。だから、誰かがコメントを書いていただければ、記事に追加します。
空間内の要素の位置は、要素を構成する5つの単位立方体の相対座標になります。座標は、基点(それぞれ座標[0,0,0])に対して取得されます。 基点の位置の主な条件は、要素上の必須位置です。そのため、この要素がキューブで満たされると、基点はキューブの基本レベルに配置されます。 基本レベルとは、アセンブリが現在行われているZ軸に沿ったレベルを意味します(以下のレベルは完全に満たされています)。 したがって、私たちは自分自身のために(そしてそれだけではなく)さらなる計算を単純化しました。
24ポジション
//x,y,z var elems=[ [[0,0,0],[1,0,0],[1,1,0],[2,1,0],[3,1,0]],//0 [[0,0,0],[1,0,0],[2,0,0],[0,0,1],[-1,0,1]],//1 [[0,0,0],[1,0,0],[1,-1,0],[2,-1,0],[3,-1,0]],//2 [[0,0,0],[1,0,0],[1,0,1],[2,0,1],[3,0,1]],//3 [[0,0,0],[1,0,0],[2,0,0],[2,-1,0],[3,-1,0]],//4 [[0,0,0],[1,0,0],[2,0,0],[2,0,1],[3,0,1]],//5 [[0,0,0],[1,0,0],[2,0,0],[2,1,0],[3,1,0]],//6 [[0,0,0],[1,0,0],[0,0,1],[-1,0,1],[-2,0,1]],//7 [[0,0,0],[0,1,0],[1,1,0],[1,2,0],[1,3,0]],//8 [[0,0,0],[0,1,0],[0,1,1],[0,2,1],[0,3,1]],//9 [[0,0,0],[0,1,0],[-1,1,0],[-1,2,0],[-1,3,0]],//10 [[0,0,0],[0,1,0],[0,2,0],[0,0,1],[0,-1,1]],//11 [[0,0,0],[0,1,0],[0,2,0],[-1,2,0],[-1,3,0]],//12 [[0,0,0],[0,1,0],[0,0,1],[0,-1,1],[0,-2,1]],//13 [[0,0,0],[0,1,0],[0,2,0],[1,2,0],[1,3,0]],//14 [[0,0,0],[0,1,0],[0,2,0],[0,2,1],[0,3,1]],//15 [[0,0,0],[0,0,1],[0,0,2],[0,1,2],[0,1,3]],//16 [[0,0,0],[0,0,1],[0,0,2],[-1,0,2],[-1,0,3]],//17 [[0,0,0],[0,0,1],[0,0,2],[0,-1,2],[0,-1,3]],//18 [[0,0,0],[0,0,1],[0,0,2],[1,0,2],[1,0,3]],//19 [[0,0,0],[0,0,1],[0,1,1],[0,1,2],[0,1,3]],//20 [[0,0,0],[0,0,1],[-1,0,1],[-1,0,2],[-1,0,3]],//21 [[0,0,0],[0,0,1],[0,-1,1],[0,-1,2],[0,-1,3]],//22 [[0,0,0],[0,0,1],[1,0,1],[1,0,2],[1,0,3]]//23 ];
組み立て順序はパズル自体によって決定されます。レベルが完全に満たされるとすぐに、ボトムアップから収集し、次のレベルに進みます。 総当たりの順序は、空間内の要素の位置の配列によって決まります。 いくつかの自由点のレベルを部分的に満たした後、位置を見つけることができない場合、前に見つかった要素は正しくないと見なされ、現在の状態とボックスが配列から削除され、検索が続行されます。
視覚化に関しては、立方体の3次元表現は、各レベルのスライスに沿って、Z軸に沿って5つのスライスの形で作成されます。
スライスは、ボックスの負でない数のセルで満たされた5x5のテーブルです。 セルはさらにパズル要素を互いに分離するために異なる色で色付けされます。 負荷を軽減するために、配列の状態は1秒に1回、または重要な瞬間に表示されます:答えが見つかったときに開始、一時停止、停止します。 さらに、「保存行」を使用して作業します。これにより、一時停止し、コードを変更し、最初からではなく一時停止場所から検索を続行できます。 また、サイクル数(アレイの現在の状態を表示する瞬間をとるサイクルの最後)、最後のサイクルの「検索」の数、および「検索」の総数を表示します。
特徴のうち、最初の起動前の準備では、各座標「ボックス」の可能な位置の配列が作成され、この時点では事前に見つけることができない位置をカットすることに注意してください。 また、汎用性のために、3つの座標すべてで「ボックス」サイズの値を変更する機能を追加しました。 視覚化の速度を上げるために、スライステーブルセルの配列を追加しました。
コメント付きの完全なコード:
-github
-JSFiddle
始めて、待って(Google Chromeで114サイクルかかり、96969659のオプションを経て)、答えを見て、実際にそれを収集します。
答え 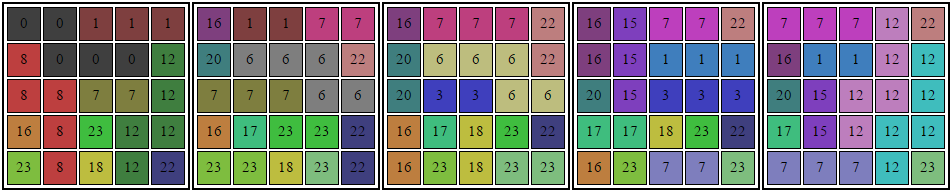

反射チェックを行いたい人のために文字列を保存
[[5,0,0,0,0]、[5,0,4,0]、[12,3,0,0]、[12,4,1,0]]
UPD Seratorのアドバイスでは、彼はWebワーカーを使用する可能性を追加しましたが、次の計算は前の計算の結果に依存するため、計算を並列化することはできません。計算自体はWebワーカーで個別に行われ、視覚化はメインストリームに残されました。
作業の結果を以下の表に示します*。 分数は、アクティブな計算タブ/非アクティブな計算タブでの計算時間を示します。 計算時のすべての追加と拡張は無効になりました。
Web Workerを使用する**:
| Google Chrome 40.0.2214.115(ハードウェアアクセラレーションなし) | 168.08秒/ 160.932秒 |
|---|---|
| Google Chrome 40.0.2214.115(ハードウェアアクセラレーション付き) | 175.644秒/ 168.802秒 |
| Yandex Browser 12/14 / 2125.10034 | 163.975秒/ 202.875秒 |
| Internet Explorer 11 | 243.778秒/ 246.766秒 |
| Mozilla Firefox 35.0.1 | 731.949秒/ 707.266秒 |
| Opera 27.0.1689.69 | 213.088秒/ 189.991秒 |
Web Workerなし:
| Google Chrome 40.0.2214.115(ハードウェアアクセラレーションなし) | 139.894秒/ 1769.311秒 |
|---|---|
| Google Chrome 40.0.2214.115(ハードウェアアクセラレーション付き) | 112.115秒/ 1738.033秒 |
| Yandex Browser 12/14 / 2125.10034 | 137.854秒/ 1901.142秒 |
| Internet Explorer 11 | 240.888秒/ 227.489秒 |
| Mozilla Firefox 35.0.1 | 173.205秒/ 2056.301秒 |
| Opera 27.0.1689.69 | 130.07秒/ 1904.973秒 |
*-作業の結果はマシンの総負荷に依存するため、表には平均値が示されています。 測定誤差は約5%でした。
**-5万回の検索ごとに視覚化のために値を送信するときに作業の結果が与えられ、他の値では結果がエラーに適合します。
ローカルWebサーバーでスクリプトを実行して、自分で確認できます。
実際のところ、計算プロセス自体の並列化は発生しなかったため、ウェブワーカーでの計算にかかった時間は、それがない場合よりも長くなりましたが、その使用はバックグラウンドで計算を実行するのに役立つ場合があります(計算タブが非アクティブの場合)。 さらに、FirefoxはWebワーカーでの計算が最も遅く、それなしで計算を実行した場合に時間的に匹敵することが判明しました。 それとは別に、Webワーカーのおかげで、視覚化をより頻繁に再描画できることに注意してください。