前回の記事で、 無秩序な集合のバイナリ操作について書いた。 この記事では、順序付きセットの実行の複雑さの少ないアルゴリズムを検討します。







内容

I.順序付きセットの交差

II。 順序付きセットの違い

III。 順序付きセットの組み合わせ

IV。 順序付きセットの対称差

おわりに

I.順序付きセットの交差

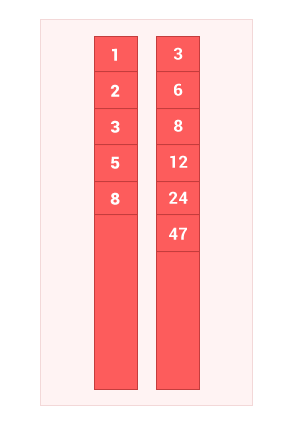
2つの順序セットAとBの共通部分は、両方のセットに同時に属する要素AとBのみを含むセットであり、重複はありません。 アルゴリズムの複雑さはO（m + n）です 。ここで、 mとnはそれぞれ入力セットAとBの長さです。



アルゴリズムの動作を示す小さなアニメーションを作成しました。





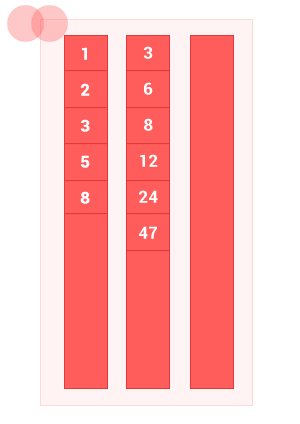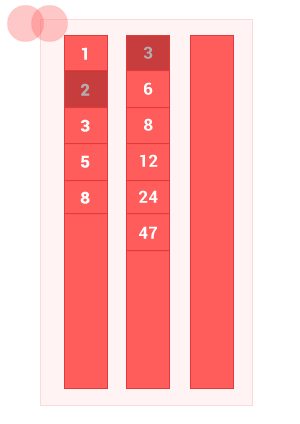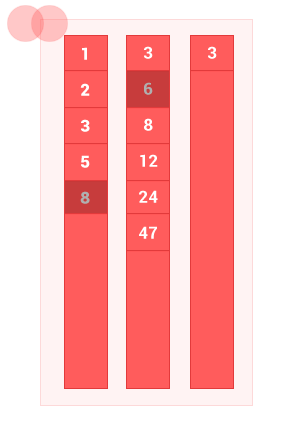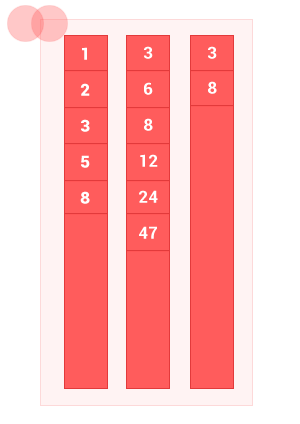
JavaScriptでの実装例：

function intersec_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) //       { if (array_1[i] == array_2[j]) { array_3[k] = array_1[i]; //     array_3 k++,i++,j++; //      3  } else { if (array_1[i] < array_2[j]) { i++; //      } else { j++; //      } } } return array_3; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

関数呼び出し：

 intersec_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); //   [3, 8]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

II。 順序付きセットの違い

2つの順序付きセットAとBの違いは、 Aの要素がBの要素と重複せずに一致しないセットです。 アルゴリズムの複雑さはO（m + n）です 。ここで、 mおよびnは、それぞれ入力順序セットAおよびBの長さです。

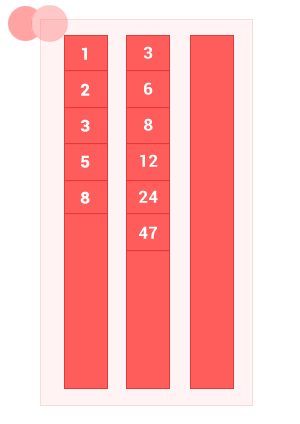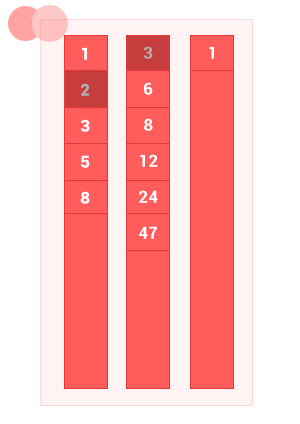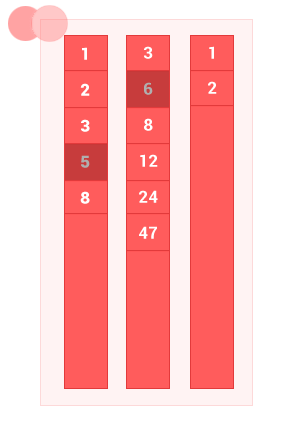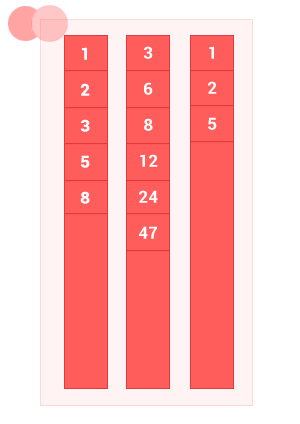
 function diff_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) //       { if (array_1[i] == array_2[j]) { i++,j++; } else { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; //      } else { j++; //      } } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } return array_3; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); //   [1, 2, 5]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

III。 順序付きセットの組み合わせ

2つの順序付けられたセットAとBの和集合は、 Aの要素とセットBの要素を持つセットであり、重複はありません。 アルゴリズムの複雑さはO（m + n）です 。ここで、 mおよびnは、それぞれ入力順序セットAおよびBの長さです。

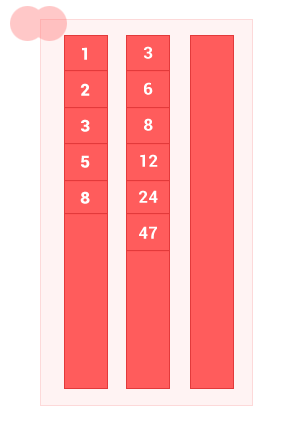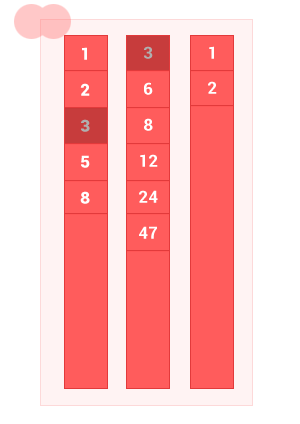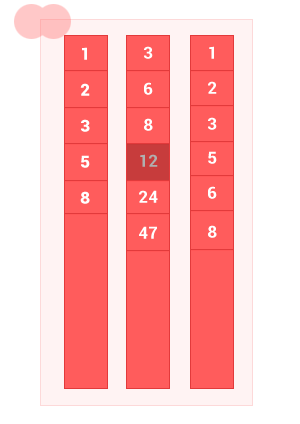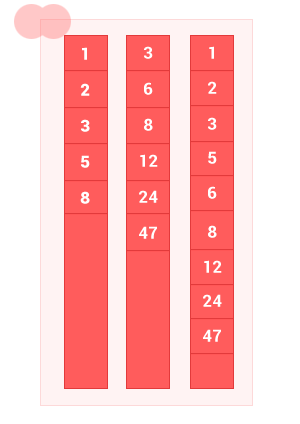
 function sum_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) //       { if (array_1[i] == array_2[j]) { array_3[k] = array_1[i]; k++,i++,j++; } else { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; //      } else { array_3[k] = array_2[j]; k++; j++; //      } } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } while (j < m) { array_3[k] = array_2[j]; k++, j++; } return array_3; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 sum_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); //   [1, 2, 3, 5, 6, 8, 12, 24, 47]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

IV。 順序付きセットの対称差

2つの順序セットAとBの対称差は、2番目の順序セットにない最初の順序セットのすべての要素と、1番目の順序セットにない2番目の順序セットの要素を含むセットです。 アルゴリズムの複雑さはO（2（m + n））です 。ここで、 mおよびnは、それぞれ入力順序セットAおよびBの長さです。



本質的に、これはセットの減算であり、最初にAからB 、次にBからAの順です。







0leGG によって提案された方法。

 symmetric_diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); //   [1, 2, 5, 6, 12, 24, 47]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

おわりに

ソートされた配列を頻繁に使用する必要があるため、これらのアルゴリズムはプロセスを大幅に高速化します。 intersec_sort_arrメソッドの実装例は、vk.comのアプリケーションにあります。 このメソッドを使用すると、数百万の要素でソートされた配列を操作する一般的なコミュニティメンバーが見つかります。このメソッドは非常に迅速に対応します。 その前に、 前の記事で説明した方法を使用しましたが、配列の処理は非常に遅くなりました。