Clever Geek Handbook

Rのオイル列

「価格チャートは過去を予測するのに最適です。」

ピーター・リンチ









どういうわけか、実際には時系列を扱う機会がなかった。 もちろん、私はそれらについて読んで、一般的な分析がどのように実行されるかについてトレーニングコースの枠組みでいくつかのアイデアを持ちましたが、統計と機械学習の教科書で言われていることは必ずしも実際の状況を反映していないことはよく知られています。



おそらく、多くは、 原油価格曲線が生み出すピルエットを関心をもって見ています 。 スケジュールは混oticとしているか、定期的すぎるように見えます。スケジュールを予測することは非常にありがたい仕事です。 もちろん、統計的、経済的、数学的、専門的手法の全力を時系列に引き下げることはできますが、もちろん、Rに基づいてテクニカル分析に対処するようにしてください。



通常の時系列で作業する場合、標準的なアプローチを使用できます。



  1. 視覚分析
  2. シリーズの拡大とそのコンポーネントの研究：季節性、周期性、傾向
  3. 数学的モデルの構築と予測










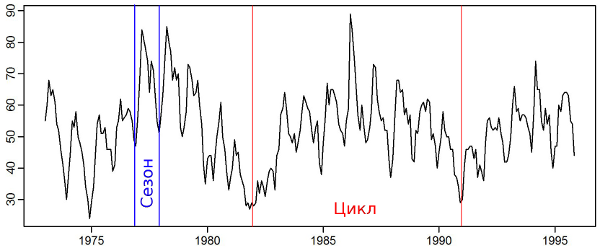
非常に便利なデータソース-Quandlがあります。 Matlab、Python、Rのインターフェースを提供します。Rの場合、1つのパッケージinstall.packages("Quandl")



インストールするだけです。 ヨーロッパのブレント原油のスポット価格 - ブレント原油のスポット価格に興味があります（以下では、3つのデータセットが異なる詳細で使用されています）。 



 library(Quandl) oil.ts <- Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="zoo") oil.tsw <-Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="zoo", collapse="weekly") oil.tsm <-Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="ts", collapse="monthly") plot(oil.tsm, xlab="Year", ylab="Price, $", type="l") lines(lowess(oil.tsm), col="red", lty="dashed")










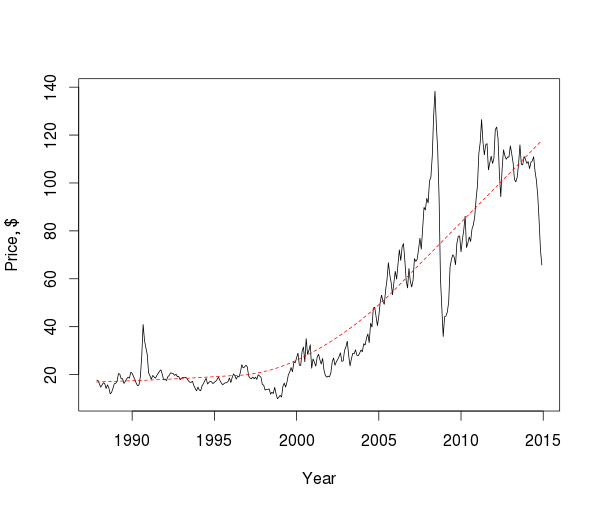
数十年規模の価格を考慮すると、いくつかのピークとフォール、およびトレンドの方向を見ることができますが、一般的に重要な結論を引き出すことは難しいため、シリーズのコンポーネントを調べます。 



 plot(decompose(oil.tsm, type="multiplicative"))












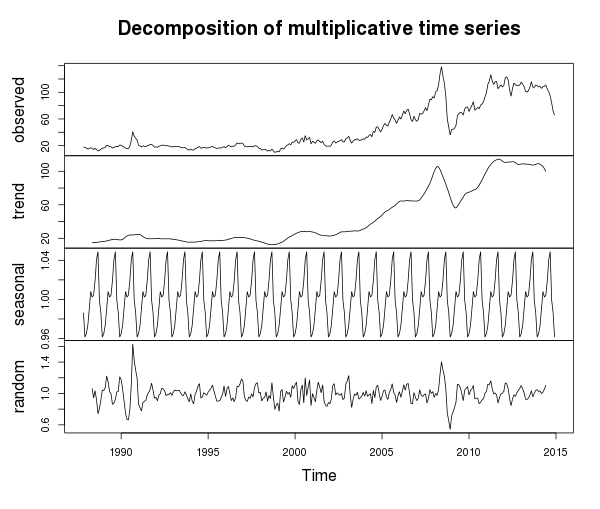
この傾向はすべて明らかなようです-21世紀には、最近まで（興味深い年を除いて）安定した成長傾向があり、多くの非定常的なものがありました -これは、 拡張Dickey-Fullerテストによって証明されています ： 



 >library(tseries) >library(forecast) >adf.test(oil.tsm, alternative=c('stationary')) Augmented Dickey-Fuller Test data: oil.tsm Dickey-Fuller = -2.7568, Lag order = 6, p-value = 0.2574 alternative hypothesis: stationary


一方、かなり高い程度の確実性で、系列の1次の差は定常的である、つまり これは統合された一次時系列です （将来この事実により、 Box-Jenkinsの方法論を適用できるようになります）。 



 >adf.test(diff(oil.tsm), alternative=c('stationary')) Augmented Dickey-Fuller Test data: diff(oil.tsm) Dickey-Fuller = -8.0377, Lag order = 6, p-value = 0.01 alternative hypothesis: stationary > ndiffs(oil.tsm) [1] 1


さらに、一般的なチャートでは見にくい季節的な要素もあることがわかりました。 よく見ると、かなり高いボラティリティに加えて、1年中に2つの価格上昇が見られます（これは、冬期とホリデーシーズンの石油消費の増加による可能性があります）。 一方、ランダムな要素があり、その重要性は特に重要な年（たとえば、2008年の金融危機）に増加します。

場合によっては、 1パラメーターのBox-Cox変換の後にデータを操作する方が望ましい場合があります。これにより、分散を安定させ、データをより標準的な形式にすることができます。 



 L <- BoxCox.lambda(ts(oil.ts, frequency=260), method="loglik") Lw <- BoxCox.lambda(ts(oil.tsw, frequency=52), method="loglik") Lm <- BoxCox.lambda(oil.tsm, method="loglik")


最も滑りやすいトピック、つまり外挿については、記事「原油価格予測手法：文学の包括的なレビュー」の著者は、期間の長さに応じて、モデルの適用可能性は次のとおりであることに注意しています。



  1. 中長期的には、非線形モデルの方が適しています-同じニューラルネットワーク、参照ベクトルマシン。
  2. 短期的には、 ARIMAはしばしばニューラルネットワークよりも優れています。


すべての手続きの後、 forecast



パッケージにnnetar()



関数を使用します。この関数を使用すると、一連のニューラルネットワークモデルを不必要な困難なく構築できます。 同時に、より詳細な（日単位）からより詳細でない（月単位）までの3つのシリーズでこれを行います。 同時に、中期的に何が起こるかを見てみましょう-たとえば、2年以上（これはチャートに青色で表示されます）。

非表示のテキスト 
 # Fit NN for long-run fit.nn <- nnetar(ts(oil.ts, frequency=260), lambda=L, size=3) fcast.nn <- forecast(fit.nn, h=520, lambda=L) fit.nnw <- nnetar(ts(oil.tsw, frequency=52), lambda=Lw, size=3) fcast.nnw <- forecast(fit.nnw, h=104, lambda=Lw) fit.nnm <- nnetar(oil.tsm, lambda=Lm, size=3) fcast.nnm <- forecast(fit.nnm, h=24, lambda=Lm) par(mfrow=c(3, 1)) plot(fcast.nn, include=1040) plot(fcast.nnw, include=208) plot(fcast.nnm, include=48)












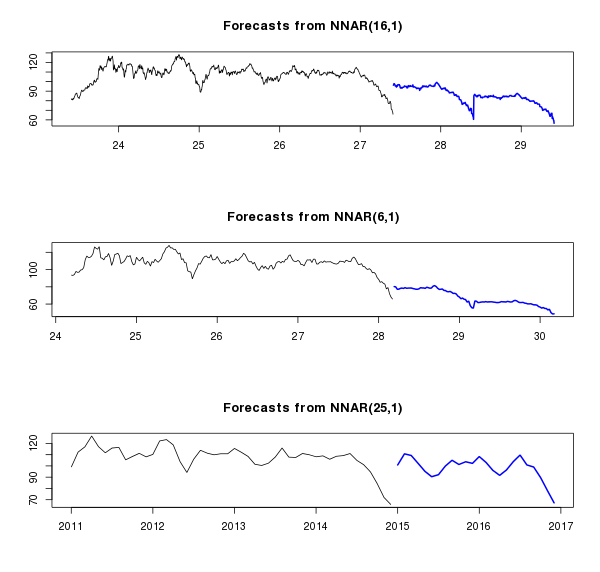
上のグラフでよくわかったのはリトレーニングです。ニューラルネットワークは行の最後のパターンをキャッチし、コピーを開始しました。 平均的なチャートでは、ネットワークは最後のパターンをコピーするだけでなく、トレンドとうまく組み合わせて、予測に現実感を与えます。 下のグラフで判明したのは、ある種の不明瞭な曲線です。 グラフは、データの平滑化に応じて予測がどのように変化するかをよく示しています。 いずれにせよ、（さまざまな理由で）高いボラティリティを持つ製品の場合、そのような期間の予測は信頼できないため、すぐに短期期間に移り 、同時にいくつかの異なるモデル（ ARIMA 、 tbat 、ニューラルネットワーク）を比較します。 過去6か月のデータを使用し、テスト目的でshort.testシリーズの12月を特に強調します。

非表示のテキスト 
 # Fit ARIMA, NN and ETS for short-run short <- ts(oil.ts[index(oil.ts) > "2014-06-30" & index(oil.ts) < "2014-12-01"], frequency=20) short.test <- as.numeric(oil.ts[index(oil.ts) >= "2014-12-01",]) h <- length(short.test) fit.arima <- auto.arima(short, lambda=L) fcast.arima <- forecast(fit.arima, h, lambda=L) fit.nn <- nnetar(short, size=7, lambda=L) fcast.nn <- forecast(fit.nn, h, lambda=L) fit.tbats <-tbats(short, lambda=L) fcast.tbats <- forecast(fit.tbats, h, lambda=L) par(mfrow=c(3, 1)) plot(fcast.arima, include=3*h) plot(fcast.nn, include=3*h) plot(fcast.tbats, include=3*h)












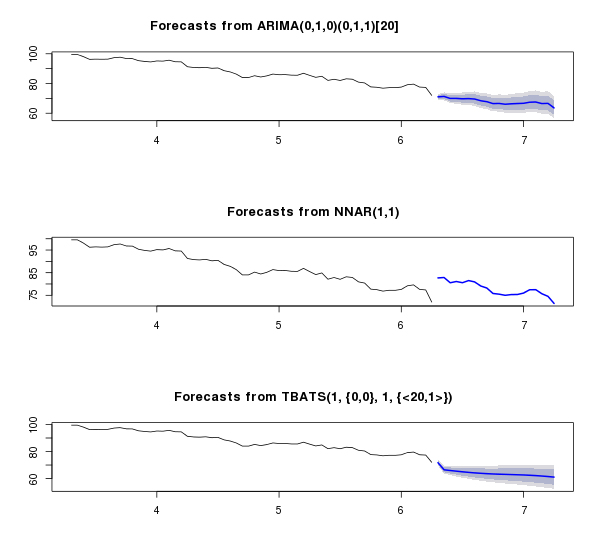
再訓練されたニューラルネットワークはややアストラルになり、ARIMAは非常に興味深い依存関係を示しました。実際の画像に近いという点で興味深いものです。 以下は、12月の各モデルの予測と実際のデータの予測と平均絶対誤差の比較です。

非表示のテキスト 
 par(mfrow=c(1, 1)) plot(short.test, type="l", col="red", lwd=5, xlab="Day", ylab="Price, $", main="December prices", ylim=c(min(short.test, fcast.arima$mean, fcast.tbats$mean, fcast.nn$mean), max(short.test, fcast.arima$mean, fcast.tbats$mean, fcast.nn$mean))) lines(as.numeric(fcast.nn$mean), col="green", lwd=3,lty=2) lines(as.numeric(fcast.tbats$mean), col="magenta", lwd=3,lty=2) lines(as.numeric(fcast.arima$mean), col="blue", lwd=3, lty=2) legend("topright", legend=c("Real Data","NeuralNet","TBATS", "ARIMA"), col=c("red","green", "magenta","blue"), lty=c(1,2,2,2), lwd=c(5,3,3,3)) grid()












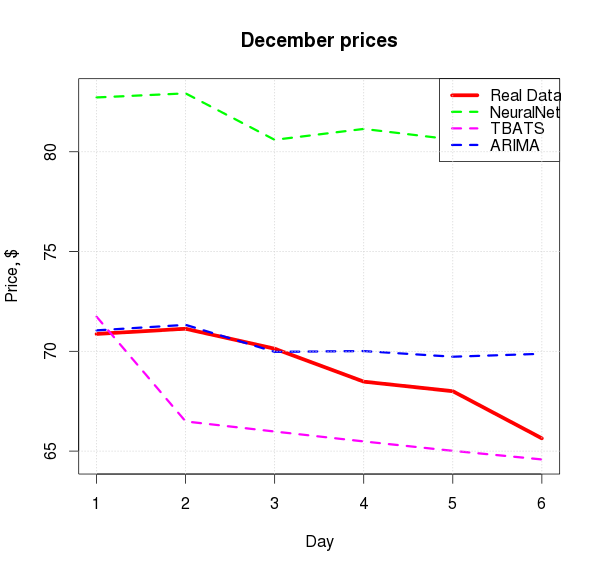
非表示のテキスト 
 mape <- function(r, f){ len <- length(r) return(sum( abs(r - f$mean[1:len]) / r) / len * 100) } mape(short.test, fcast.arima) mape(short.test, fcast.nn) mape(short.test, fcast.tbats)




有馬 NNet TBATS
1.99％ 18.26％ 4.00％




結論の代わりに



長期的な予測についてはコメントしません。この状況ではすでに予測が間違っていることは明らかです。 しかし、ARIMAは短期的には非常に良い結果を示しました。 次の事実にも注意を払う価値があります。 石油の価格下落：



  1. 9月には5％。
  2. 10月-10％
  3. 11月-15％
  4. 12月に...？


これは、原油価格を変更するプロセスが、ランダムなパラメーターによって規制されるプロセスとはかけ離れていることを示唆しているようです。


More articles:


All Articles