
このような興味深いタスクがあります-画像(写真)のセットから3D構造を構築する-モーションからの構造。 どうすれば解決できますか? 考えた後、そのようなアルゴリズムが思い浮かびます。 すべての画像で特徴的な特徴(ポイント)を見つけ、それらを互いに比較し、それらを三角測量して、それらの3次元座標を見つけます。 本当に問題があります-撮影時のカメラの位置は不明です。 それらを見つけることができますか? 可能のようです。 実際、フレームごとにNポイント、 Mフレームがあるとします。 その後、未知数は3 * N (ポイントの3次元座標)+ 6 *(M-1) (カメラの座標(6の代わりに異なる数がありますが、本質は変わりません))になります。 2 * M * Nの方程式があります(各画像の各点には2つの座標があります)。 すでに2つの画像と6つのポイントについては、問題は解決可能であることがわかります。 カットの下には、SfM問題を解決するための概念スキームの説明があります(可能であれば、式なしで-しかし、思慮深い研究へのリンクを使用して)。
計画はこれです:
- キーポイントを見つける
- 連続する画像のペアのポイント間の対応を見つける(ただし、すべての画像のペアを見つけることができます)
- 誤った一致を除外する
- 連立方程式を解き、カメラの位置とともに3次元構造を見つけます
計画はシンプルでわかりやすいようです。 そして、もちろん、3番目と4番目のポイントの全体の陰謀。
1.ポイント
ポイントを見つけても問題は発生しません。 たくさんの方法があります。 最も有名なのはSIFTです。 スケールと方向(任意のカメラの動きにとって重要)を考慮して、キーポイントを確実に見つけます。 このメソッドには、いくつかのオープンソース実装があります。
2.コンプライアンス
各ポイントには、その説明(記述子)を添付する必要があります。 異なる画像内のポイントの記述子が近い場合、同じ物理オブジェクトであると想定できます。 最も単純な記述子は、ポイントの小さな近傍です。 しかし理想的には、もちろん、記述子は画像のスケールや向きに依存しないものでなければなりません。 SIFTメソッドはまさにこれを使用します。 次に、一致の検索は、1つの画像のすべてのキーポイントをバイパスし、別の画像で最も近い記述子を検索するようになります。
3.誤一致のフィルタリング
記述子の品質にかかわらず、多くの誤った一致があることは明らかです。 それらはフィルタリングする必要があります。 ここでは、2つの段階を区別できます。
- ジオメトリに依存しないフィルタリング
- エピポーラフィルタリング
ジオメトリに依存しないフィルタリングは、同じSIFTメソッドで説明されています。 たとえば、いくつかの単純なフィルターがあります。最初の画像から2番目の画像への最適な一致は、2番目から1番目の画像への最適な一致に一致する必要があります。

エピポーラジオメトリ。 CおよびC 'はカメラの光学中心です。 最初の画像の点Pがmに投影される場合。 次に、別の画像で、直線l ' mでの投影を検索する必要があります。
もちろん、最も強いフィルタリングは、 エピポーラ制限を使用することです。 その幾何学的な意味は、ある画像内の各ポイントに対して、別の画像内の対応するポイントが特定のライン上にあるということです(これは、ポイントの真の3次元座標に依存しません)。 数学的には、この特性は方程式m T Fm '= 0で表されます 。 ここで、 m =(u、v、1) Tは画像内のキーポイントの同次座標であり 、 Fは基本行列です。 最も重要なことは、この比率は、観察されるシーンの3次元構造に依存しないことです。
基本マトリックスがわからないため、次の方法を使用して、誤った一致をフィルタリングできます。
- 複数のポイントをランダムに選択し、そこから基本行列を計算します(計算方法については、[1]、セクション14.3.2で説明しています)。
- 与えられた精度で条件m T Fm '= 0を満たすポイントがさらにいくつあるかを計算します。
- ポイントの数が十分に大きい場合はサイクルを停止し、そうでない場合はポイント1に進みます。
この単純なアルゴリズムはRANSACと呼ばれ、タスクに最適です。 そして、はい-彼はまだ非常にunningであり、あなたは彼を苦しめることもできます。 まあ、またはOpenCVを使用できます。
4.三次元構造の検索
最後に、空間内のポイントが画像内のポイントとどのように接続されているかを確認します。 ここではすべてが単純です-射影変換。 幸いなことに、私のタスクの詳細(小さな視野の望遠鏡による観察)により、カメラのアフィンジオメトリを使用することが可能になりました。 カメラの幾何学的パラメーターは2つの部分で構成されています。
- 空間内のカメラの位置を決定する外部パラメーター(回転行列R 3x3およびシフトベクトルt 3x3)。
- CCDカメラの画像デザインを決定する内部パラメーター。 これには、各軸に沿ったスケーリング、軸間の角度、および高次の歪み係数が含まれます。 正方形ピクセルとアフィンカメラを使用する場合、パラメーターkのみが残ります。
観測方程式( (X、Y、Z) T点の3次元座標と画像内の位置(u、v) Tの関係 )は、次のように記述できます。
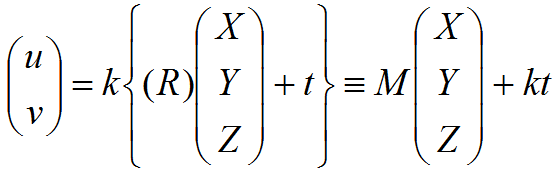
アフィンジオメトリでは3番目の行が無視され、回転行列とシフト行列から使用できるのは2行のみであることに注意することが重要です。
この比率がすべてのポイントに対してできるだけ正確に実行されるように、すべてのカメラの外部(および内部)パラメーターとポイントの3次元座標を選択する必要があることがわかります。
この問題を解決するには2つの方法があります。 1つ目は、この非線形システムを集合非線形法で解こうとすることです( バンドル調整 )。 ここでの主な問題は明らかです-非線形方程式の非常に大きなシステムを解く(または、多次元空間の非線形関数を最小化する)ことができ、正しい解への収束を達成する必要があります。 別の方法は、可能であれば問題を分析的に解決することです。 だからやる。
そして、ここで因子分解法は私たちの助けになります。 特異分解を使用すると、すべてのカメラからすべてのポイントが見える場合のアフィンカメラの問題を解決できることがわかります(実際には、これは「画像の各ペアごとに」を意味します)。 正当化は、[1]、セクション18.2に記載されています。
- 重心が原点になるように、すべての画像上のすべての点をシフトしましょう。 これにより、シフトベクトルを方程式から完全に除外できます。
- 見つかったすべての点の射影から観測行列を構成します
 。 次に、行列Mにすべてのカメラ行列を、行列Xに互いに隣り合うすべての3次元ポイントをすべて書き込むと、方程式W = MXが得られます。
。 次に、行列Mにすべてのカメラ行列を、行列Xに互いに隣り合うすべての3次元ポイントをすべて書き込むと、方程式W = MXが得られます。 - 特異分解W = UDV Tを見つけます。 次に、 Uの最初の3列からカメラ行列が取得され、特異値が乗算されます。 3次元アフィン構造は、行列Vの最初の3列から取得されます。
簡単すぎる? はい-キャッチがあります。 事実は、私たちの解決策はアフィン変換まで見つかったということです。 回転行列の構造を無視しました(それはまったくarbitrary意的ではありません)。 状況を改善するには、カメラが直交行列で記述されていること、または単に直交行列CについてW = MX = MCC T Xであることに注意する必要があります (方法は[2]、セクション12.4.2で説明されています)。
回転行列は、次の条件を満たす必要があります。
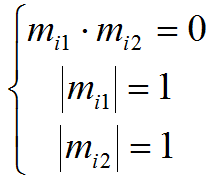
ここで、 m ijは各カメラの行列の行です。 これらの制限を使用して行列Cを見つけることができます。これにより、アフィン構造がユークリッドになります。
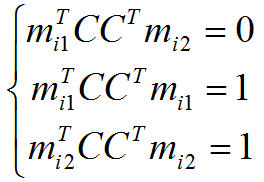
この連立方程式はCに関しては非線形ですが、 D = CC Tに関しては線形です。 Dから、行列Cは 、行列の平方根を取得することによって取得されます。 右側のカメラの行列にCを乗算し、左側の3次元構造にC Tを乗算すると、正しいユークリッド構造が得られ、これも観測行列を満たします。
さて、最後の1つは、異なるカメラペアの3次元構造の結合です。 わずかなニュアンスがあります。 取得したカメラの位置は、ポイントのセットに対して中心にあり、カメラの異なるペアでは、ポイントのセットは異なります。 そのため、2組のカメラで交差するポイントのセットを見つける必要があります。 次に、座標を再計算するには、これらのポイントセット間の変換を見つけるだけです。
そこで、3次元ユークリッド(つまり、セグメントの長さの角度と関係を保存する)構造を取得しました。 投稿の冒頭の画像には、Energy-Buranモデルの構造があります(以下のソース画像の1つ)。 この構造はスパースと呼ばれます。 ポイントが比較的少ない。 この構造から密度を上げてテクスチャを引き出すことは、別の話です。

文学
- R. Hartley、A。Zisserman、「コンピュータービジョンにおけるマルチビュージオメトリ」
- フォーサイス、ポンス。 「コンピュータービジョン。 現代のアプローチ”