タスクは何ですか
まず、私たちが話していることを思い出させてください。 機械学習の主なツールの1つは、ベイズの定理です。
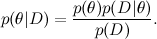
ここで、 Dはデータ、θはトレーニングするモデルパラメーター、
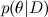-これは、利用可能なデータDの影響を受けるθの分布です。 以前の記事のいずれかで、ベイズの定理についてすでに詳しく説明しました。 機械学習では、通常、事後分布を見つけたい 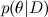そして、新しい変数値を予測します 
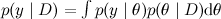。 複雑なグラフィックモデルでは、これらすべては、前のシリーズで説明したように、通常、さまざまなランダム変数の大きくて混乱した分布があるという事実に帰着します。 
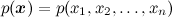、これはより単純に分布の積に分解され、私たちの仕事は辺縁化 、つまり 変数の一部を合計するか、変数の一部から関数の期待値を見つけます。 すべてのタスクは、複雑な分布、通常はいくつかの変数の値が代入されるモデルの条件付き分布の条件下で、さまざまな関数の数学的期待値を計算することになります。 また、任意の時点で結合分布の値を数えることができると想定できます。これは通常、モデルの一般的な形式から簡単に得られ、困難はこれらの変数をまとめて統合することです。
正確な結論を出すことは困難であり、有効なアルゴリズムが得られるのは、サイクルのないまたは小さなサイクルのファクターグラフの場合のみです。 ただし、実際のモデルには、多くの場合、互いに密接に関連し、大量のサイクルを形成する一連の変数が含まれています。 発生する困難を克服するための1つの可能な方法-変分近似について少し話しました。 そして今日、私はもう一つの、より一般的な方法-サンプリングについて話します。
モンテカルロアプローチ
アイデアは極端に単純です。 原則として、必要なものはすべて、複雑で混乱を招く分布p （ x ）のさまざまな関数の期待値の形で表現されることを既に知っています。 分布関数の期待値を計算する方法は？ この分布からサンプリングできる場合、つまり ランダムポイントを取る
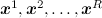分布p （ x ）に従って、任意の関数の期待値は、サンプリングされたポイントでの算術平均として近似できます。
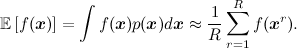
たとえば、平均（期待）を計算するには、サンプルxの平均をとる必要があります。
したがって、実際にすべてのタスクは、分布によってポイントをサンプリングする方法を学習することになります。ただし、この分布の値を任意のポイントで読み取ることができます。
難しさは何ですか
1つの変数の機能で育った人（つまり、大学で基本的な分析のコースを受講した人なら誰でも）には、ここでは大きな問題はなく、これらすべての何もないことについての会話は、積分を概算する方法を知っていますセグメントをパーツに分割し、各小さなセグメントの中央で関数を計算し、そこにある長方形、台形を計算するだけです...そして、実際には、1つの変数からの分布からサンプリングするのに複雑なことはありません。 いつものように、困難はディメンションの増加から始まります-ディメンション1で、間隔をサイド0.1のセグメントに分割するために関数の10個の値をカウントする必要がある場合、ディメンション100ではそのような値には10,100が必要になり、これは非常に悲しいことです。 通常の2-3次元とはまったく異なり、高次元で作業を行うこの効果やその他の効果は、次元の呪いと呼ばれていました。 他の興味深い直観に反する効果があります。おそらくいつかこのことについてもっと詳しく話すべきです。
もう1つ難点があります-私は上で、いつでも分布値を読むことができると書きました。 実際、通常、分布p （ x ）の値ではなく、 p （ x ）に比例する関数p * （ x ）の値を考慮することができます。 ベイズの定理を思い出してください-それから、事後分布自体ではなく、それに比例する関数が得られます。
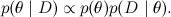
通常、この場所ではこれで十分であると言いました。確率の正確な値は、結果の分布を正規化して単純に計算することができます（つまり、ベイズの定理で分母を計算します）。 ただし、これはまさに複雑な分布のすべての値を要約するという現在の解決方法を学ぼうとしている難しいタスクです。 したがって、実際には、真の確率の値を当てにすることはできず、それらに比例する関数p *のみを当てにすることができます。
対処方法：チャートの下のサンプル
上記のすべての困難にもかかわらず、サンプリングは依然として可能であり、これは実際に近似出力の主な方法の1つです。 さらに、すぐにわかるように、サンプリングは見た目ほど難しくありません。 このセクションでは、すべてのサンプリングアルゴリズムが何らかの形で基づいている基本的な考え方について説明します。 考え方は次のとおりです。分布密度関数pのグラフの下の点を均等に選択すると、そのX座標は分布pから取得されます。 直観的に理解するのは非常に簡単です。密度グラフを想像して、このような小さな列に分割します（グラフはmatplotlibで作成されます）。
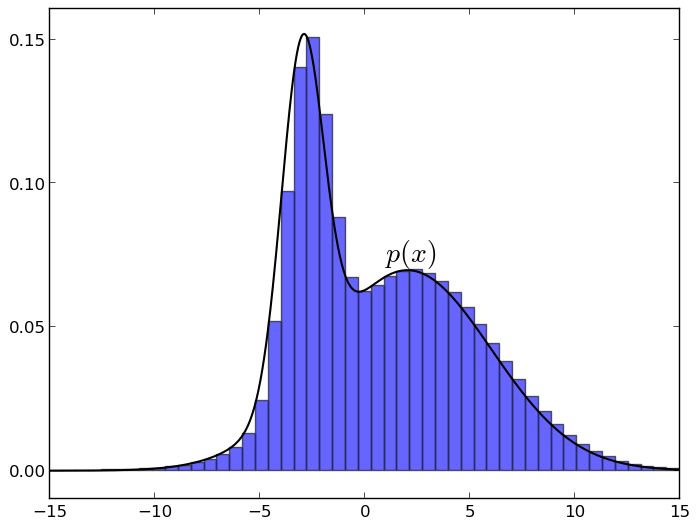
グラフの下でランダムなポイントを取得すると、各X座標がその列の高さに比例する確率で満たされることは明らかです。 この列の密度関数の値だけで。
したがって、必要な分布の密度グラフの下でランダムポイントを取得する方法を学習するだけで済みます。 これを行う方法は？
実際に機能し、実際にしばしば適用される最初のアイデアは、いわゆる拒絶サンプリングです。 他の分布q （より正確には、それに比例する関数q * ）があると仮定しましょう。これは、サンプリング方法を既に知っています。 通常、これはある種の古典的な分布-均一または正規です。 ここで、正規分布からのサンプリングも完全に些細な作業ではないことに注意する価値がありますが、ここではスキップします。今では「人々はこれを行う方法を知っている」ことを知るだけで十分です。 さらに、すべてのxについて定数cを知っていると仮定します。
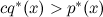。 次に、この方法でpをサンプリングできます。
- 分布q * （ x ）でサンプルxを取得します。
- 間隔から一様に乱数uを取る
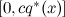; - p * （ x ）を計算します。 それがuより大きい場合、 xがサンプルに追加され、それより小さい場合（つまり、 uが密度グラフp *に該当しなかった場合）、 xは逸脱します（したがって、サンプルに偏差があります）。
以下は、偏差のあるサンプル（正規分布、他の2つのガウス分布の混合をメジャー化するように選択された）を示す図です。
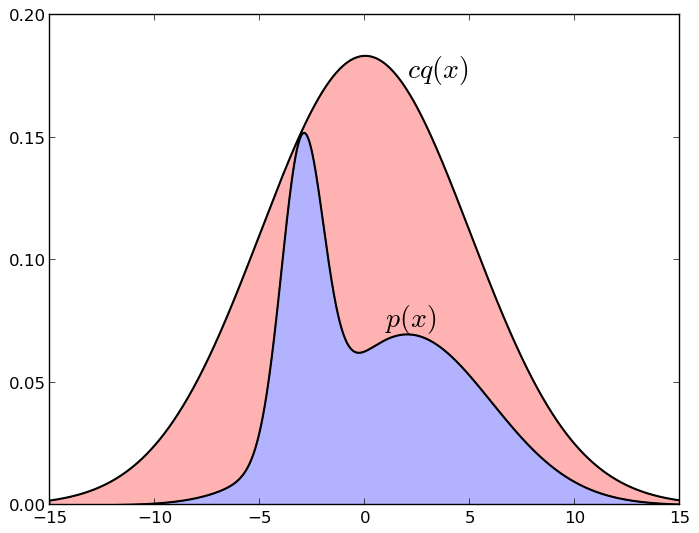
グラフcq *の下の点がグラフp *の下にある場合、つまり ブルーゾーンに入れます。 そしてそれ以上の場合、すなわち レッドゾーンに-私たちはそれを取らない。 繰り返しますが、これがなぜ機能するのかを直感的に理解するのは簡単です。cq *グラフの下にランダムなポイントを均等に取り、 p *グラフの下にあるポイントのみを同時に残します。この場合、スケジュールp * 。 同様に、 pに十分に近いqを選択した場合（たとえば、 pが集中している場所を大まかに知っており、この領域をガウス分布でカバーしている場合）、この方法は単にスペース全体を同一の断片に分割するよりもはるかに効果的であることも明らかです。 しかし、メソッドが機能するためには、 cqが実際にpを非常によく近似している必要があります-青いゾーンの面積が赤の面積の10 -10である場合、サンプルは機能しません...
このアイデアにはさまざまなバージョンがありますが、詳細は説明しません。 要するに、このアイデアとそのバリエーションは、ユニット単位の複雑な密度でうまく機能しますが、実際には高次元では困難が始まります。 次元の呪いの影響により、 qの古典的な試行分布はさまざまな不快な特性を取得します（たとえば、高次元では、オレンジの皮はほぼ全体の体積を占有し、特に、正規分布は非常に薄い「皮」にほぼ完全に集中します。ゼロ）、適切な場所のサンプルを取得できず、すべてが失敗することがよくあります。 他の方法が必要です。
Metropolis-Hastingsアルゴリズム
このアルゴリズムの本質は、同じ考えに基づいています。関数グラフの下で均等にポイントを取りたいです。 ただし、アプローチは異なります：関数qの 「キャップ」で分布全体をカバーしようとする代わりに、内側から行動します：関数グラフの下でランダムウォークを構築し、あるポイントから別のポイントに移動し、時々現在のウォークポイントをサンプルとして取得します。 この場合、このランダムウォークはマルコフチェーンであるため（つまり、次のポイントは前のポイントのみに依存し、メモリはありません）、このクラスのアルゴリズムはMCMCサンプリング（マルコフチェーンモンテカルロ）とも呼ばれます。 Metropolis-Hastingsアルゴリズムが実際に機能することを証明するには、マルコフ連鎖の特性を知る必要があります。 しかし、今は正式に何かを証明するつもりはないので、ウィキへのリンクを残しておきます 。
実際、アルゴリズムは偏差のある同じサンプルに似ていますが、重要な違いがあります：以前は、 qの分布は空間全体で同じでしたが、現在は局所的であり、現在のさまよう点に応じて時間とともに変化します。 前と同様に、トライアル分布のファミリーを検討します
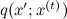どこで 
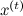-現在の状態。 しかし、現在qはpの近似値ではなく、現在のポイントの近くに集中しているサンプリングされた分布のようなものである必要があります。たとえば、分散が小さい球面ガウス分布が適しています。 新しい状態xの候補は 'からサンプリングされます 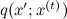。 アルゴリズムの次の反復は状態から始まります 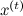また、次のもので構成されます。
- 分布によりxを選択 ;
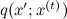- 計算する
（怖がる必要はありませんが、
ガウス分布などの対称分布の場合、これは1に等しく、これは非対称性の単なる補正です）。 - 確率a （ a > 1の場合、 1）
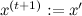そうでなければ 
。
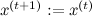一番下の行は、次のステップを踏むと新しい分布センターに移動し、分布pに応じてランダムウォークを取得することです。この方向で密度関数が増加する場合は常にステップをとり、減少する場合はそれを拒否することがあります（常に拒否するわけではありません）なぜなら、局所的な最大値から抜け出し、グラフ全体をさまようことができる必要があるからですp ）。 ちなみに、ステップが拒否された場合、新しいポイントを単に破棄するのではなく、同じx （ t ）を 2回繰り返します-したがって、より高い密度に対応する分布pの局所的最大値の周りでサンプルを繰り返す可能性が高いことに注意してください。
繰り返しになりますが、この写真は、2つの2次元ガウス分布の混合グラフの下の平面上を移動する典型的なものです。
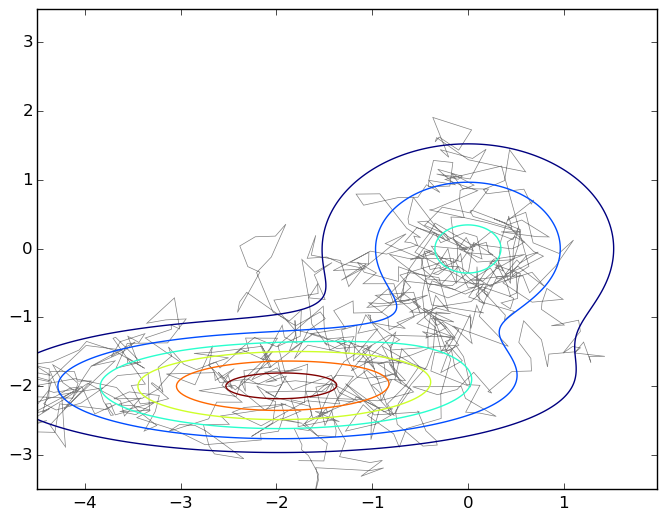
このアルゴリズムの実際の単純さを強調するために、このグラフを生成したコードを示します。
Pythonコード
import numpy as np import matplotlib.pyplot as plt import matplotlib.patches as patches import matplotlib.path as path import matplotlib.mlab as mlab import scipy.stats as stats delta = 0.025 X, Y = np.meshgrid(np.arange(-4.5, 2.0, delta), np.arange(-3.5, 3.5, delta)) z1 = stats.multivariate_normal([0,0],[[1.0,0],[0,1.0]]) z2 = stats.multivariate_normal([-2,-2],[[1.5,0],[0,0.5]]) def z(x): return 0.4*z1.pdf(x) + 0.6*z2.pdf(x) Z1 = mlab.bivariate_normal(X, Y, 1.0, 1.0, 0.0, 0.0) Z2 = mlab.bivariate_normal(X, Y, 1.5, 0.5, -2, -2) Z = 0.4*Z1 + 0.6*Z2 Q = stats.multivariate_normal([0,0],[[0.05,0],[0,0.05]]) r = [0,0] samples = [r] for i in range(0,1000): rq = Q.rvs() + r a = z(rq)/z(r) if np.random.binomial(1,min(a,1),1)[0] == 1: r = rq samples.append(r) codes = np.ones(len(samples), int) * path.Path.LINETO codes[0] = path.Path.MOVETO p = path.Path(samples,codes) fig, ax = plt.subplots() ax.contour(X, Y, Z) ax.add_patch(patches.PathPatch(p, facecolor='none', lw=0.5, edgecolor='gray')) plt.show()
そのため、密度グラフp （ x ）の下でランダムウォークを取得しました。 実際、これはまだ証明する必要がありますが、数学には進まないので、一言。 このランダムウォークをどうするか、独立したサンプルが必要です。ここで、ウォークの次のポイントは確かに前のポイントの隣にあり、独立の痕跡はまったくないことがわかります。
答えは簡単です。すべてのポイントを取得する必要はありませんが、いくつかのポイントのみを取得する必要があります。 これはランダムウォークであるため、 qのほとんどが半径εに集中し、 pが集中する合計半径がDに等しい場合、独立したサンプルを取得するには、順序付けが必要になります。
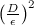ステップ。 繰り返しになりますが、一言で説明するか、ポイントがnステップでどれだけ進むかという確率論のコースから古典的な問題を思い出すことができます。 彼女は平均して去る 
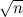、したがって、ステップの数が2次になることは論理的です。
そして今、主な機能：この2 次数は2つの分布の半径に依存しますが、次元にはまったく依存しません 。 モンテカルロマルコフチェーンサンプリングは、私たちが議論した他の方法よりも次元の呪いの影響をはるかに受けません。 それが、ゴールドスタンダードになった理由の1つです。 ただし、実際にはDを評価するのは難しいため、特定の実装では通常これを行います。まず、特定の数の最初のステップ、たとえば1000が破棄されます（これはバーンインと呼ばれ、これは非常に重要です。開始点が失敗する可能性があるためです。 p 、したがって、プロセスを開始する前に、十分に長く歩いていることを確認する必要があります）、各n番目のサンプルを取得します。ここで、 nはサンプルのシーケンスの実際の自己相関に基づいて実験的に選択されます。
ギブスサンプリング
そして、今日の最後のサンプリングアルゴリズムはギブスサンプリングです。 これは実際、Metropolis-Hastingsアルゴリズムの特別なケースであり、非常に一般的でシンプルな特別なケースです。
Gibbsによるサンプリングのアイデアは非常に単純です。非常に大きな次元にあり、ベクトルxが非常に長く、サンプル全体を一度に選択するのが難しいと仮定すると、うまくいきません。 サンプルを一度にすべて選択するのではなく、コンポーネントごとに選択してみましょう。 次に、これらの1次元分布がより簡単になることが確実になるため、サンプルを選択します。
正式に言えば、ベクトルのコンポーネントを実行します
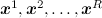、各ステップで1つを除くすべての変数を修正し、順次選択します 
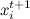配布による
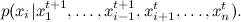
これは、座標軸の1つに沿って各ステップで移動するという点で、メトロポリスヘイスティングスをさまよう一般的なケースとは異なります。 対応する画像を次に示します。
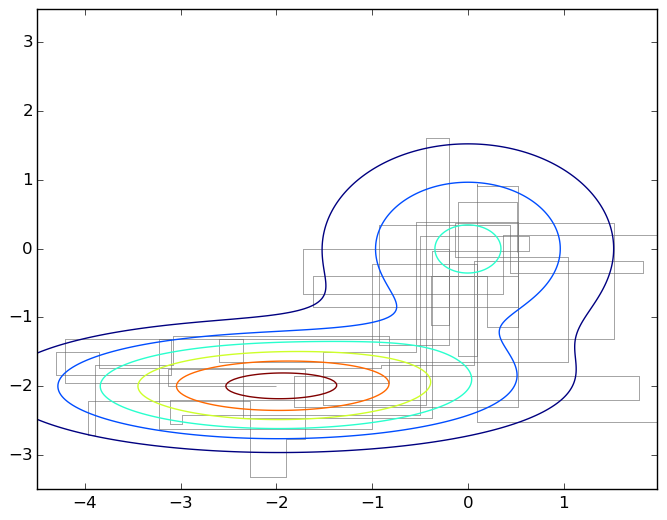
ギブスサンプリングは、分布のメトロポリスアルゴリズムの特殊なケースです。
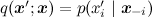、各サンプルを受け入れる確率は常に1に等しくなります（これは演習として証明できます）。 したがって、ギブスサンプリングは収束し、これは実際には同じランダムウォークであるため、同じ2次推定値が当てはまります。
Gibbsサンプリングに特別な前提や知識は必要ありません。 作業モデルをすばやく作成できるため、非常に一般的なアルゴリズムです。 また、大きな次元では、一度に複数の変数をサンプリングするよりも一度に複数の変数をサンプリングする方が効率的である可能性があることに注意してください-たとえば、ある共有のすべての変数が別の共有のすべての変数に関連付けられている変数の二部グラフがあることがよくあります（または多くの場合）が、互いに関連していません。 そのような状況では、神自身が1つの共有のすべての変数を修正し、別の共有のすべての変数を同時にサンプリングするように命じました（これは文字通り取ることができます-そのような構造では、1つの共有のすべての変数が別の条件の下で条件付きで独立しているため、独立して並行してサンプリングできます）、すべてを修正しますセカンドビート変数など。
おわりに
今日、私たちは多くのことを管理しました。さまざまなサンプリング手法について話しました。これは、複雑な確率モデルの近似推論のための主要なツールの1つです。 さらに、この新しいミニサイクルをテーマモデリング、より正確にはLDAモデル（潜在ディリクレ割り当て、潜在ディリクレ割り当て）に向けて開発する予定です。 次のシリーズでは、モデル自体について説明し （ 既に簡単に説明しましたが 、今ではさらに詳しく説明できます）、ギブスサンプリングがLDAでどのように機能するかを説明します。 そして、LDAとその推奨システム用の多くの拡張機能を適用する方法に徐々に進みます。