ビジネスで想像上の価値を使用するために、彼らはすでに賞を与えています。 今では、 デュアルから何かを持っていることは興味深いです。

双対数は、 a +εbの形式の実数（またはその他の複素数など）のフィールドの拡張です。ここで 、 aとbは元のフィールドの数値です。 εε= 0と仮定します 。

このような奇妙な数字には実用的な用途があることがわかります。



二重数の主な有用な特性は

f（a +εb）= f（a）+εf '（a）b 。

f（x）の式があれば、微分f '（x）を取得するのは簡単です。 ただし、 f（x）は 、アルゴリズムの形式でのみ使用できます。たとえば、特別に構成された線形方程式のシステムの解としてです。 εが追加された初期データでアルゴリズムを実行することにより、パラメーターの1つに関する結果と導関数の値を取得します。

ちょっとした数学

正式には、二重数はリングではなく、フィールドを形成します-明らかに、それらの中にはゼロ除数があります。 しかし、0による除算を引き起こさずに実数で「良い」問題が解決される場合、双対でも解決されます。 したがって、この記事の枠組みの中で、数学的厳密さを無視し、二重数をフィールドと見なします。



εの係数が互いに乗算しないことは簡単にわかります。つまり、元のフィールド上の任意のモジュール（ベクトル空間）からのものである可能性があります。 この場合、いくつかの引数に関して偏導関数を取得できます。



素数の数には行列表現があります 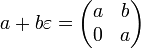。 一般化のために、マトリックスは2対角に変換されますが、さらに演算を行うと三角形になります。 2番目の対角線より上の係数は、パラメーターの相互作用に関する情報を保持します-一部の問題では、これは重要な情報になる場合がありますが、今では無視します。

行列表現は、線形代数問題で元の数の代わりに双対の行列表現を「入力」できるという点で興味深いです。 私はこのアプローチを深く探求していません。 パラメーターの数が問題の次元に匹敵する場合に興味があり、この場合、計算の複雑さが非常に急速に増大します。 このアプローチの利点は、既製の高品質の線形代数ライブラリを使用できることです。

実装

残念ながら、BLASおよびLAPACKに基づく標準ライブラリは、実数または複素数でのみ機能します。 そのため、純粋なHaskellで書かれたライブラリを探し始めました。これは、異なる表現での作業が通常と見なされるかなり一般的な言語です。 しかし、失望が待っていました-Floating型クラスで動作する唯一のパッケージ（分数ではない理由は明らかではありません-線形代数の正弦余弦は本当に必要ない）は線形であることが判明しました。 そして、私にとって最も興味深い操作は、最大4x4までのサイズの行列に対してのみ実装されています。



実験のために、2進数の簡単な実装と線形方程式のプリミティブソルバーを作成しました。これについて簡単に説明します。

ソースコードはこちらから入手できます 。



二重数を表すためのデータ型は次のとおりです。

data GDual nv = !n :+- (vn)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのパラメーターは、ソースフィールドの表現のタイプと、ベクトルεを表現するためのパラメーター化されたコンテナーです。 コンテナは線形パッケージのAdditive型クラスを表すと暗黙的に想定されています。



Numの実装は非常に馬鹿です。

 instance (Eq n, Num n, Additive v) => Num (GDual nv) where fromInteger x = (fromInteger x) :+- zero (x1 :+- y1) + (x2 :+- y2) = (x1 + x2) :+- (y1 ^+^ y2) (x1 :+- y1) - (x2 :+- y2) = (x1 - x2) :+- (y1 ^-^ y2) (x1 :+- y1) * (x2 :+- y2) = (x1 * x2) :+- ((y1 ^* x2) ^+^ (x1 *^ y2)) negate (x :+- y) = (negate x) :+- (y ^* (-1)) abs (a@(x :+- y)) = case (signum x) of 0 -> 0 :+- fmap abs y z -> ((z * x) :+- (x *^ y)) signum (x :+- y) = case (signum x) of 0 -> 0 :+- fmap signum y z -> z :+- zero
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ゼロ（ 0：+ -...）の近傍のabsおよびsignumの場合、型クラスで宣言された関係は違反されます

 abs x * signum x == x
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

しかし、他の時点でそれは持続します。

absの実装は、可能な場合に関係f（a +εb）= f（a）+εf '（a）bが保持されるように行われます。



フラクショナル実装：

 instance (Num (GDual nv), Fractional n, Additive v) => Fractional (GDual nv) where (x1 :+- y1) / (x2 :+- y2) = (x1 / x2) :+- ((y1 ^/ x2) ^-^ ((x1 / (x2 * x2)) *^ y2)) recip (x :+- y) = (recip x) :+- (y ^/ (x * x)) fromRational x = (fromRational x) :+- zero
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

除算は完全に完了しているわけではありません-可能な場合でもゼロの近傍から数値で除算することはできません（Additive型クラスはこれに必要な機能を提供しません）。 しかし、私のアプリケーションの領域では、このような区分はありません。この場合、通常の数で計算すると、0/0の区分が発生します。



何らかの理由で線形が必要だったフローティング実装は愚かであり、私はそれを持ち込みません。

GDualは、ニアザーのEpsilon型クラスもnearZeroメソッドを使用して実装します。

 Math.GDual.Demo.SimpleSparseSolver.solve :: (Fractional t1, Ord t, Epsilon t1) => [[(t, t1)]] -> [[(t, t1)]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

方形スパース行列で表される線形方程式系を解きます。 マトリックスは、係数マトリックスと右側の列の連結です。 基本操作による解法は、行列を恒等式に導きます-この場合の右側は答えになります。

備考

関数の導関数は、パラメーターの変化またはエラーに対する関数値の感度を示します。 ただし、同時に、関数の計算プロセスでは丸め誤差は考慮されません。 これらのエラーは、数値の別の一般化によって考慮することができます： 区間演算