はじめに
ハミング距離は、同じ長さの線の異なる位置の数です。 たとえば、HD( 1 0 0、0 0 1 )= 2。
ハミング距離を計算する問題は、1969年にMinskyとPapertによって初めて提起されました[1]。タスクは、要求されたハミング距離までの指定されたハミング距離内にあるすべての行をデータベースから検索することでした。
このようなタスクは非常に簡単ですが、その効果的な解決策の検索はまだ課題です。
ハミング距離は、既に近い複製の検索、パターン認識、ドキュメント分類、エラー修正、ウイルス検出などのさまざまなタスクにすでに広く使用されています。
たとえば、Mankuと仲間は、ハミング距離の計算に基づいてWebドキュメントのインデックスを作成するときに重複をクラスタリングする問題の解決策を提案しました[2]。
ミラーと友人はまた、与えられたオーディオフラグメントで曲を検索する概念を提案しました[3]、[4]。
同様のソリューションが画像検索と網膜認識のタスクに使用されました[5]、[6]など。
問題の説明
サイズnのバイナリ文字列Tのデータベースがあり、各文字列の長さはmです。 要求された文字列aおよび必要なハミング距離k 。
タスクは、距離k内にあるすべての行を検索することです。
アルゴリズムの元の概念では、静的および動的の2つのバージョンの問題が考慮されます。
-静的問題では、距離kは事前に事前に決定されています。
-反対に、動的では、必要な距離は事前にわかりません。
この記事では、静的問題のみの解決策について説明しています。
静的タスクのHEngineアルゴリズムの説明
この実装は、 k <= 10内の文字列の検索に焦点を当てています。
静的問題には、線形スキャン、クエリ拡張、データベース拡張の3つのソリューションがあります。
この場合、 クエリ拡張とは、元の行の特定の距離に収まる行のすべての可能なバリアントの生成を指します 。
データベースを拡張すると 、このデータベースの複数のコピーが作成され、必要な距離の要件を満たすすべての可能なオプションが生成されるか、データが他の方法で処理されます(これについては後で詳しく説明します)。
HEngine [8]は、これら3つの方法の組み合わせを使用して、メモリとランタイムを効果的にバランスさせます。
理論のビット
このアルゴリズムは、以下を示す小さな定理に基づいています。
2つのラインaとbの距離がHD( a 、 b )<= kの場合、セグメンテーション係数を使用してrcutメソッドによってラインaとbをサブストリングに分割すると
r > =⌊k /2⌋+ 1
距離が1を超えない場合、HD( a i、 b i)<= 1の場合、少なくともq = r -⌊k /2⌋の部分文字列が必ず存在します。
rcutメソッドによる基本文字列からの部分文字列の選択は、次の原則に従って実行されます。
条件を満たすセグメンテーション係数と呼ばれる値が選択されます
r > =⌊k /2⌋+ 1
最初のr- ( m mod r )部分文字列の長さは⌊m / r⌋で、最後のm mod r部分文字列は⌈m / r⌉です。 ここで、 mは文字列の長さで、⌊は最も近い一番下に丸められ、⌉は最も近い上に丸められます。
これは同じことですが、例のみがあります。
長さm = 8ビットの2つのバイナリ文字列が与えられます:A = 11110000およびB = 11010001、それらの間の距離はk = 2です。
セグメンテーションファクターr = 2/2 + 1 = 2を選択します。つまり、長さm / r = 4ビットの合計2つのサブストリングがあります。
a1 = 1111、a2 = 0000
b1 = 1101、b2 = 0001
対応するサブストリング間の距離を計算すると、少なくとも( q = 2-2/2 = 1)1つのサブストリングが一致するか、その距離が1を超えることはありません。
私たちが見るもの:
HD(a1、b1)= HD(1111、1101)= 1
そして
HD(a2、b2)= HD(0000、0001)= 1
基本文字列の部分文字列は、 署名と呼ばれていました 。
署名または部分文字列a1およびb1(a2およびb2、a3およびb3 ...、arおよびb r )は互いに互換性があると呼ばれ、異なるビットの数が1以下の場合、これらの署名は一致と呼ばれます。
また、HEngineアルゴリズムの主なアイデアは、一致する署名を見つけるようにデータベースを準備し、必要なハミング距離内にある行を選択することです。
データベースの前処理
文字列を部分文字列に正しく分割すると、少なくとも1つの部分文字列が対応する部分文字列と一致するか、異なるビット数が1を超えない(署名が一致する)ことは既にわかっています。
つまり、データベースからすべての行を徹底的に検索する必要はありませんが、最初に一致する署名を見つける必要があります。 部分文字列は最大で1つ異なります。
しかし、部分文字列で検索する方法は?
バイナリ検索方法はこれをうまくやるはずです。 ただし、文字列のリストをソートする必要があります。 しかし、1行からいくつかの部分文字列を取得します。 部分文字列のリストに対してバイナリ検索を実行するには、各リストを事前にソートする必要があります。
したがって、これはデータベースを拡張する方法、つまり、それぞれが独自のサブストリングまたはシグネチャ用の複数のテーブルを作成する方法を要求します。 (そのようなテーブルは署名テーブルと呼ばれます 。そして、そのようなテーブルの全体は署名のセットです )。
アルゴリズムの元のバージョンは、選択されたサブストリングが最初の場所にあるように、サブストリングの順列も記述します。 これは、実装を容易にし、アルゴリズムをさらに最適化するために行われます。
行Aがあります。これは3つのサブストリングa1、a2、a3に分割されており、順列の完全なリストはそれぞれ次のようになります。
a1、a2、a3
a2、a1、a3
a3、a1、a2
次に、これらの署名テーブルがソートされます。
検索の実装
この段階では、データベースを前処理した後、ソートされたテーブルのコピーがいくつかあり、それぞれが独自のサブストリングに対応しています。
明らかに、最初に部分文字列を見つけたい場合は、署名テーブルを作成するのと同じ方法で、要求された文字列から署名を取得する必要があります。
また、必要なサブストリングが最大で1つの要素で異なることもわかっています。 そして、それらを見つけるには、クエリ拡張メソッドを使用する必要があります。
言い換えると、選択された部分文字列は、この部分文字列自体を含むすべての組み合わせを生成する必要があり、その場合、差は最大で1つの要素になります。 このような組み合わせの数は、部分文字列の長さ+ 1に等しくなります。
そして、完全に一致するかどうか、対応する署名テーブルでバイナリ検索を実行します。
このようなアクションは、すべてのサブストリングおよびすべてのテーブルに対して実行する必要があります。
そして最後に、指定されたハミング距離の制限に収まらないラインを除外する必要があります。 つまり 見つかった行で線形検索を実行し、条件HD( a 、 b )<= kを満たす行のみを残します。
ブルームフィルター
著者は、ブルームフィルター[7]を使用してバイナリ検索の数を減らすことを提案しています。
ブルームフィルターを使用すると、誤検出の割合が少ないテーブルに部分文字列が含まれているかどうかをすばやく判断できます。 これは、テーブルハッシュよりも高速です。
テーブル内のサブストリングのバイナリ検索の前に、フィルターがこのサブストリングがこのテーブル内にないことを返す場合、検索する意味がありません。
したがって、署名テーブルごとに1つのフィルターを作成する必要があります。
著者はまた、この方法でブルームフィルターを使用すると、クエリの処理時間が平均57.8%短縮されることに注意しています。
今、同じこと、例だけで
8ビット長のバイナリ文字列のデータベースがあります。
11111111
10000001
00111110
タスクは、ターゲットビット10111111までの異なるビットの数が2を超えないすべてのラインを見つけることです。
したがって、必要な距離はk = 2です。
1.セグメンテーション係数を選択します。
式に基づいて、セグメンテーションファクターr = 2を選択します。これは、1つのストリングから2つのサブストリングのみが存在することを意味します。
2.一連の署名を作成します。
部分文字列の数は2なので、作成する必要があるテーブルは2つだけです。
T1およびT2
3.ソースへのリンクを維持しながら、対応するテーブルにサブストリングを保存します。
T1 T2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4.テーブルを並べ替えます。 それぞれ個別に。
T1
0011 => 00111110
1000 => 10000001
1111 => 11111111
T2
0001 => 10000001
1110 => 00111110
1111 => 11111111
この前処理は完了しました。 そして、検索に進みます。
1.要求された文字列の署名を取得します。
検索文字列10111110は署名に分割されます。 それぞれ1011と1100で、最初は1番目のテーブル、2番目は2番目のテーブルです。
2. 1つ異なるすべての組み合わせを生成します。
オプションの数は5です。
2.1最初の部分文字列1011の場合:
1011
0 011
1 1 11
10 0 1
101 0
2.2 2番目の部分文字列1100の場合:
1100
0 100
1 0 00
11 1 0
110 1
3.バイナリ検索。
3.1最初に生成された最初の部分文字列1011のすべてのバリアントについて、最初のテーブルで完全一致のバイナリ検索を実行します。
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
2つのサブストリングが見つかりました。
3.2ここで、2番目の部分文字列1100のすべてのバリアントについて、2番目のテーブルでバイナリ検索を実行します。
1100
0100
1000
1110 == 1110 => 00111110
1101
部分文字列が1つ見つかりました。
4.結果を1つのリストに結合することにより:
00111110
11111111
5.コンプライアンスを直線的にチェックし、不適切な条件<= 2を除外します。
HD(10111110、00111110)= 1
HD(10111110、11111111)= 2
両方の行は、2つ以下の要素の差の条件を満たす。
この段階では線形検索が実行されていますが、候補のリストはまったく大きくないことが予想されます。
候補の数が多くなる状況では、HEngineの再帰バージョンを使用することが提案されています。
明らかに
図1は、検索アルゴリズムの例を示しています。
文字列の長さが64で、距離制限が4の場合、セグメンテーションファクターはそれぞれ3で、1行あたり3つの部分文字列のみです。
T1、T2、およびT3は、サブストリングB1、B2、B3、21、21、および22ビット長のみを含む署名テーブルです。
要求された文字列は部分文字列に分割されます。 次に、対応するサブストリングの署名範囲が生成されます。 最初と2番目の署名の場合、組み合わせの数は22になります。最後の署名には23のオプションがあります。 そして最後に、バイナリ検索が実行されます。
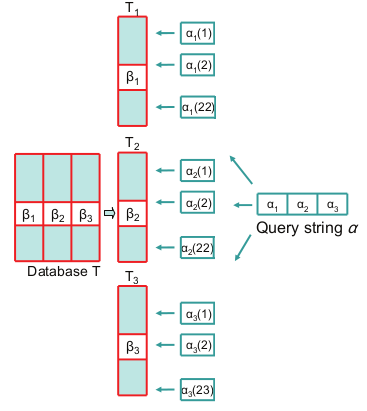
図1.署名テーブルへのクエリの処理を簡略化したバージョン。
結果
平均的なケースでのこのようなアルゴリズムの複雑さはO ( P *(log n + 1))です。ここで、 nはデータベース内の行の総数、log n + 1はバイナリ検索、 Pはバイナリ検索の数です。テーブルごとの組み合わせの数にテーブルの数を掛けた値: P =(64 / r + 1)* r
極端な場合、複雑さは線形を超える場合があります。
このアプローチは4.65で使用するメモリが少なく、[2]で説明した以前の作業よりも16%高速であることに注意してください。 そして、与えられた制限内のすべての行を見つけることは、現在知られているものから最速の方法です。
実装
もちろん、これはすべて魅力的ですが、実際に触れるまでスケールを評価することは困難です。
HEngine [9]のプロトタイプが作成され、利用可能な実際のデータでテストされました。
tests$ ./matches 7 data/db/table.txt data/query/face2.txt Reading the dataset ........ done. 752420 db hashes and 343 query hashes. Building with 7 hamming distance bound ....... done. Building time: 12.964 seconds Searching HEngine matches ....... found 100 total matches. HEngine query time: 0.1 seconds Searching linear matches ....... found 100 total matches. Linear query time: 6.828 seconds
752420でのデータベースからの343ハッシュの検索には約0.1秒かかり、これは線形検索よりも60倍速いため、結果は満足のいくものでした。
ここでやめることができるようです。 しかし、私は実際のプロジェクトでなんとかしてそれを使用したかったのです。
実際に使用する前にワンクリック
画像ハッシュのデータベースとPHPのバックエンドがあります。
タスクは何とかしてHEngineとPHPの機能を接続することでした。
FastCGI [10]の使用が決定されました。投稿habrahabr.ru/post/154187およびhabrahabr.ru/post/61532は、この点で私を大いに助けてくれました。
PHPから、以下を呼び出します。
$list = file_get_contents( 'http://fcgi.local/?' . $hashes );
約0.5秒で結果が返されます。 線形検索に9秒かかり、MySQLへのクエリを通じて、少なくとも20秒かかる場合。
マスターした皆さんに感謝します。
参照資料
[1] M.ミンスキーとS.ペーパー。 パーセプトロン。 MIT Press、ケンブリッジ、MA、1969。
[2] GS Manku、A。Jain、およびAD Sarma。 Webクロールのニアデュプリケートを検出します。 Procで 16th WWW、2007年5月。
[3] MLミラー、MAロドリゲス、およびIJコックス。 オーディオフィンガープリント:高次元のバイナリ空間での最近傍探索。 MMSP、2002年。
[4] MLミラー、MAロドリゲス、およびIJコックス。 オーディオフィンガープリンティング:高次元のバイナリ空間での最近傍検索。 Journal of VLSI Signal Processing、Springer、41(3):285–291、2005年。
[5] J. Landr´eおよびF. Truchetet。 バイナリハミング距離による画像検索。 Procで 第2回VISAPP、2007年。
[6] H. YangおよびY. Wang。 ハミング距離制約のあるLBPベースの顔認識方法。 Procで 第4回ICIG、2007年。
[7] B.ブルーム。 許容エラーを伴うハッシュコーディングのスペース/時間のトレードオフ。 ACMの通信、13(7):422-426、1970。
[8] Alex X. Liu、Ke Shen、Eric Torng。 大規模ハミング距離クエリ処理。 ICDE会議、ページ553-564、2011年。
[9] github.com/valbok/HEngine C ++でのHEngineの実装
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp FastCGIを介してハッシュを検索するためのラッパープログラムの例。