D.ポイア
はじめに
数学は、離散と連続の2つの世界に分かれています。 現実の世界では、これと他の場所があり、多くの場合、1つの現象の研究にさまざまな角度からアプローチできます。 この記事では、生成関数を使用して問題を解決する方法を検討します。離散世界から連続世界へ、そしてその逆へと続く橋です。
関数を生成するという考え方は非常に簡単です。シーケンス<g 0 、g 1 、g 2 、...、g n >を離散オブジェクト、べき級数g 0 + g 1 z + g 2 z 2 + ... + g n z nに関連付けます+ ...-オブジェクトは連続的であるため、数え切れないほどの数学的分析ツールを問題の解決策に結び付けます。 通常、生成関数によって生成されたシーケンスが生成されると言われています。 これはシンボリック構成である、つまり、zシンボルの代わりに、加算および乗算演算が定義されるオブジェクトが存在する可能性があることを理解することが重要です。
製造機能の歴史
イギリスの数学者アブラハム・デ・ムアヴルが関数を生成する方法の基礎を築いたことが知られており、この方法のさらなる開発と継続は、レオナルド・オイラーという名前の偉大な数学者に委ねられています。
18世紀の50年代に、オイラーは次の問題を解決しました。20、2 1、2 2 、...、2 nグラムの重量を使用してどのような商品を計量できますか？ この問題を解決するために、彼は当時知られていない関数を生成する方法を使用しました。 関数を生成するデバイスの詳細を説明した後、このタスクに戻ります。
関数の生成方法
単純なタスクで多くの問題を解決できるこの強力なメカニズムの研究を開始します。 黒と白のボールを合計でn個並べる方法はいくつありますか。
白い記号を○、黒い記号-●、T n-希望するボールの位置数で示します。 記号Ø-ボールの数がゼロであることを示します。 組み合わせ問題の解決策と同様に、ささいなケースから始めます。
n = 1の場合、明らかに2つの方法があります-白いボール○を取るか、黒いボール●を取るかのいずれかなので、T 2 = 2です。
n = 2の場合、配置には4つの方法があります：○○、○●、●○、●●。
n = 3の場合を考えます。 白いボールから始めて上記の4つの組み合わせを続けることができます○○○、○○●、○●○、○●●、または黒いボールから始めて同様に4つのボールを続けることができます●○○、●○ ●、●●○、●●●。
その結果、ボールの数は2倍になりました。つまり、T 3 = 2T 2です。 同様に、T 4 = 2T 3 、つまりすべてのnを一般化すると、この問題の解である再帰方程式T n = 2T n-1が得られます。 この方程式の解は簡単に推測できます-T n = 2 n （2⋅2n -1 = 2 nなので）。
しかし、推測が悪い場合はどうでしょうか？ そして、方程式がより複雑な場合はどうなりますか？ 一般的に、生成関数はどこから来ますか？
ボールの配置のすべての可能な組み合わせを「要約」します。
G =Ø+○+●+○○+○●+●○+●●+○○○+○○●+○●○+○●●+●○○+●○●+●●○+●● ●+ ...
このような不合理な一見合計の許容性の問題は省略されています。 ボールのシーケンスを追加および乗算します。 さらに、すべてが明確になっていますが、ボールのシーケンスを別のシーケンスで乗算するとはどういう意味ですか？ 掛ける○●による●○は、○●●○以上のものを得ません。 ただし、ボールの積は数字の積とは対照的に、可換ではありません。なぜなら、○●●●○≠●○⋅○● 作業中の記号Ø-は乗法単位の役割、つまりØ⋅○○●=○○●⋅Ø=○○●の役割を果たし、ボールの任意のシーケンスと交換します。
シリーズGで一連の操作を実行します。つまり、左の白と黒のボールを取り出します。
G =Ø+○（Ø+○+●+○○+○●+●○+●●+ ...）+●（Ø+○+●+○○+○●+●○+●●+。 ..）=Ø+○G +●G
方程式G =Ø+○G +●Gを取得します。
乗算は非可換であり、実際には左除算と右除算を区別しないという事実にもかかわらず、私たちは自分の危険とリスクでこの方程式を「解決」しようとします。 取得します
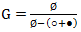
等比数列の合計の式が与えられる
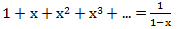、私たちは持っています
。
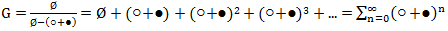この合計は、可能なすべての分割オプションを1回だけ考慮します。 次に、Newton二項式を使用します。
どこで 
nとkの組み合わせの数です。 次に、これを考慮に入れて、次のことを行います。
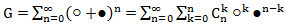
○ k ● nkでの係数は、n x kの組み合わせの数に等しく、k個の量の○ボールとnk個の数のボールを含むn個のボールのシーケンスの総数を示します。 したがって、n個のボールの位置の総数は、kのすべての可能な値の合計です。 知られているように
。
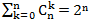この式は、次から直接取得できます。
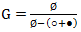Øを1に、○と●をzに置き換えます（同等の観点から）。 ゲット 
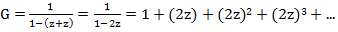つまり、z nの係数は2 nです。
方法論
それでは、この方法をさまざまな問題の解決に役立てることができるのはなぜですか？
この問題を解決するためのアルゴリズムは、おおよそ次のように説明できます。最終的な形式のべき級数G（z）= g 0 + g 1 z + g 2 z 2 + ... + g n z n + ...および係数g k （明示的に指定されていない）-元の問題を解決するための鍵です。 シリーズが形式的であるという事実は、z-が単なるシンボルであることを示しています。つまり、数字、ボール、ドミノボーンなど、その代わりに任意のオブジェクトが存在する可能性があります。 分析におけるべき級数とは異なり、正式なべき級数には数値が与えられていないため、数値引数に対するそのような級数の収束について話すことは意味がありません。
G（z）= g 0 + g 1 z + g 2 z 2 + ... + g n z n + ...-は、シーケンス<g 0 、g 1 、g 2 、...、g n >の生成関数と呼ばれます。 ただし、G（z）は関数ですが、それでも正式な表記法であることに注意してください。つまり、G（0）= g 0なので、z = 0以外の値z = z 0をzに置き換えることはできません。
次に、無限和G（z）を使用してさまざまな変換を行い、それを閉じた（コンパクトな）形式に変換します。 つまり、生成関数には2つの表現があります：無限と閉じています。原則として、問題を解決するには、無限形式を閉じた形式に変換してからべき級数で閉じた形式を展開し、係数g kの値を取得する必要があります。
冒頭に提示された質問に答えると、これを言うことができます：このメソッドの成功は、生成関数を閉じた形で書く能力に関連しています。 したがって、たとえば、無限形式のシーケンス<1、1、1、...、1>の生成関数は、1 + x + x 2 + x 3 + ...として表されます。
。
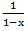そして、知識を持って、オイラーが解決した課題に戻りましょう。
したがって、タスクは次のとおりです。20、2 1、2 2 、...、2 nグラムの重みとメソッドの数を使用して、どの重みを計量できますか？
オイラーがこの問題の解決策を考案した期間はわかりませんが、その予想外の点で印象的です。 自分で判断してください。 オイラーは積G（z）=（1 + z）（1 + z 2 ）（1 + z 4 ）...を考慮します。これは、括弧を開いた後、無限級数G（z）= 1 + g 1 z + g 2 z 2として表されます。 + g 3 z 3 + ....
係数g kは何ですか？ 各g kはz kの係数であり、z kはいくつかの単項式z 2mの積として取得されます。つまり、g kは、数1、2、2 2のいくつかの合計としてのkの異なる表現の数です。 2 3 、...、2 m 、.... 言い換えれば、g kは、指定された重量で負荷をkグラムで計量する方法の数です。 まさに私たちが探していたものです！
オイラーの次のステップは前のステップと同じです。 彼は方程式の両側に（1-z）を掛けます。
（1-z）G（z）=（1-z）（1 + z）（1 + z 2 ）（1 + z 4 ）（1 + z 8 ）...
（1-z）G（z）=（1-z2）（1 + z 2 ）（1 + z 4 ）（1 + z 8 ）...
（1-z）G（z）=（1-z 4 ）（1 + z 4 ）（1 + z 8 ）...
（1-z）G（z）= 1
一方では、G（z）= 1 + g 1 z + g 2 z 2 + g 3 z 3 + ...一方、
。 最後の等式は、幾何学的進行の合計に他なりません。 
。 これら2つの等式を比較すると、g 1 = g 2 = g 3 = ... = 1が得られます。つまり、kグラム単位の荷重は、1、2、4、8、...グラムの重みで独自の方法で計量できます。
再発関係の解決
生成関数は、組み合わせの問題だけでなく、解決にも適しています。 繰り返しの関係を解決するために使用できることがわかりました。
おなじみのフィボナッチ数列から始めましょう。 私たちはそれぞれ、その反復形式を知っています：F 0 = 0、F 1 = 1、F n = F n-1 + F n-2 、n≥2。しかし、誰もがこの形式の閉じた形式を知っているわけではなく、これは驚くことではありません。結局のところ、その構成には無理数（「黄金比」）が含まれています。
だから私たちは
F 0 = 0、
F 1 = 1
F n = F n-1 + F n-2 、n≥2
各行にz 0 、z 1 、...、z nをそれぞれ乗算します。
z 0⋅F 0 = 0、
z 1⋅F 1 = z、
z n⋅F n = z n⋅F n-1 + z n⋅F n-2 、n≥2
これらの平等を要約します。
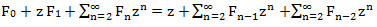
左側を示します
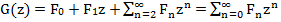
右側の各用語を検討してください。
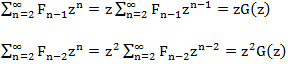
次の方程式がありますG（z）= z + z G（z）+ z 2 G（z）
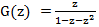フィボナッチ数列の生成関数です。
それを最も単純な分数の合計に分解します。これのために、方程式の根を見つけます。
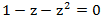。 この単純な2次方程式を解くと、次のようになります。 
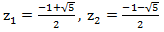。 次に、生成関数を次のように分解できます。
次のステップは、係数aおよびbを見つけることです。 これを行うには、分数に共通分母を掛けます：
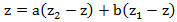
値z = z 1およびz = z 2をこの方程式に代入すると、
最後に、生成関数の式を少し変換します
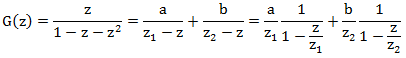
現在、各分数は等比数列の合計です。
式に従って
見つける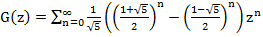 
しかし、次の形式のG（z）を探していました。
。 このことから、
この式は、「黄金比」を使用せずに別の形式に書き換えることができます。
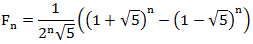
美しい再帰方程式を考えると、これは予想するのに十分困難でした。
生成関数を使用して再帰方程式を解くための一般的なアルゴリズムを書きましょう。 それは4つのステップで書かれています：
- シーケンスの他の要素を通してgnを表す1つの方程式を書き留めます。 この式は、g -1 = g -2 = .... = 0であるという事実を考慮して、すべての整数nに対して有効なままでなければなりません。
- 方程式の両側にz nを乗算し、すべてのnを合計します。 左側に金額が表示されます
、生成関数G（z）と等しい。 右側は、G（z）を含む他の式になるように変換する必要があります。 - G（z）の閉じた式を取得して、結果の方程式を解きます。
- べき級数のG（z）を展開し、z nの係数を読み取ります。これはg nの閉形式になります。
この方法が機能する理由は、単一の関数G（z）がシーケンスg n全体を表し、この表現が多くの変換を可能にするためです。
次の例に移る前に、便利なことが多い関数の生成時に実行される2つの操作を検討します。
生成関数の差別化と統合
関数を生成するために、導関数の通常の定義は次のように書くことができます。
G = G（z）を生成関数とします。 この関数の導関数は関数と呼ばれます
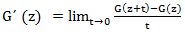。 微分は明らかに線形操作であるため、関数の生成にどのように作用するかを理解するには、変数の程度でその作用を調べるだけで十分です。 私たちは持っています
したがって、任意の生成関数に対する微分の作用
G（z）= g 0 + g 1 z + g 2 z 2 + g 3 z 3 + ...は、G΄（z）= g 1 + 2g 2 z + 3g 3 z 2 + 4g 4 z 3 + ...
積分は関数です
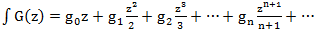
微分操作は、統合操作の逆です。
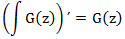
導関数を積分すると、自由項がゼロの関数が得られるため、結果は元の関数とは異なります。
べき級数の形式で表現可能な関数の場合、微分の式は通常の式に対応することがわかります。 積分の式は、上限が可変の積分値に対応します
生成関数の微分と統合で得られた知識を使用して、次の再帰方程式を解こうとします。
g 0 = 1
g 1 = 1
g n = g n-1 + 2g n-2 +（-1） n
上記のアルゴリズムに従います。 アルゴリズムの最初の条件が満たされています。 すべての等式の両側に適切な程度までzを掛けて、合計します。
z 0⋅g 0 = 1
z 1⋅g 1 = z、
z n⋅g n = z n⋅g n-1 + 2z n⋅g n-2 +（-1）n⋅z n
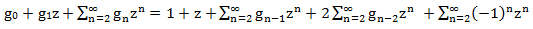
左側
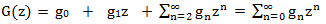無限形式の生成関数です。
右側をG（z）で表現しようとします。 各用語を考慮してください：
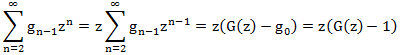
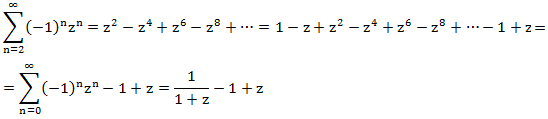
方程式を作成します。
これは、特定の再帰方程式の生成関数です。 それを単純な分数に展開すると（たとえば、不定係数の方法や、zのさまざまな値を代入する方法によって）、次のようになります。
2番目と3番目の項は簡単にべき級数に分解されますが、最初の項を少し修正する必要があります。 生成関数の差別化のルールを使用すると、次のことができます。
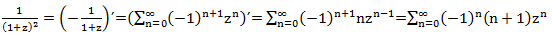
実際にはすべて。 べき級数の各用語を展開し、答えを取得します。
一方では、G（z）を次の形式で検索しました
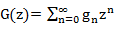一方、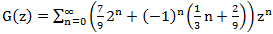 
。
手段
。
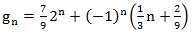結論の代わりに
生成関数は、さまざまな性質のオブジェクトのセットをリスト、配布、および分割するなど、多くの実用的な問題を解決する強力な武器であるため、数学に大きな用途があります。 さらに、生成関数を使用すると、他の方法では入手が非常に難しい組み合わせ式を証明できます。 たとえば、関数分解
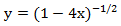べき級数の形式は 
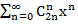、つまり、等式は真です。
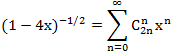
この平等の両側を二乗すると、
左側と右側のx nの係数を等しくすると、次のようになります。
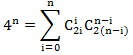
この式には透明な組み合わせの意味がありますが、証明するのは簡単ではありません。 20世紀の80年代に、この問題に特化した出版物がありました。