線形バイナリ分類問題を検討します（問題が線形に分離できない場合、対称積分L-2カーネルを使用して問題に還元できます（ SVMを参照）。
このような問題を解決する場合、分類された要素（以下、サンプルと呼びます）は、次元nのベクトル空間の要素として表されます。 実際には、このような問題では、nは非常に大きくなる可能性があります。たとえば、遺伝子を分類するタスクでは、数万になることがあります。 大きな次元では、計算時間が長くなるだけでなく、数値計算の誤差が大きくなる可能性があります。 さらに、大きなディメンションを使用するには、大きな実験コストがかかる場合があります。 問題は、サンプルの重要でない成分を破棄してnを減らすことで、新しいスペースでサンプルが「悪くない」（線形的に分離可能）または「それほど悪くない」ように分離できるかどうかです。
私の記事では、この記事Gene_Selection_for_Cancer_Classification_usingのメソッドの簡単な概要から始めて、自分のメソッドを提案します。
Gene_Selection_for_Cancer_Classification_usingのアルゴリズム
Gene_Selection_for_Cancer_Classification_usingの次元削減方法の主なアイデアは、すべてのコンポーネントをランク付けすることです。 次のアルゴリズムが提案されています。
- すべての（残りの）コンポーネントにいくつかの重みを割り当てます（方法-以降）
- すべてのサンプルから最小重量のコンポーネントを捨てます。
- SVMをトレーニングします。 サンプルを分離できない場合は、最後のステップでスローされたコンポーネントを返し、アルゴリズムを終了します;そうでない場合は、スローされたコンポーネントのないデータでステップ1に進みます。
基本的に、この記事では、取得したSVMの重みを割り当てる方法、つまり、対応するコンポーネントの分類関数の係数を重みとして使用する方法を検討します。 SVMをトレーニングした後、分類関数（w、x）+ b = 0が得られた場合、wiコンポーネントはコンポーネントiの重みになります。 この記事では、重みを設定する相関方法についても説明していますが、他の方法と同様に、SVM方法に負けています。 ステップ1に戻ると、ステップ3からSVMメソッドの重みがわかります。
そのようなアルゴリズムのクラスは、大規模なサンプルでSVMをトレーニングすることを強制されています。 エラーと速度の問題は解決されません。 彼が提供するのは、SVMのトレーニング後に分類されたサンプルのコンポーネントの数を減らす機会です。 削減されたコンポーネントの値を実験的に取得するのに費用がかかる場合は、節約できます。
PSさらに、wiのような重みの選択は非常に物議を醸しています。 少なくとも、すべてのサンプルのコンポーネントiのサンプル分散またはすべてのサンプルのコンポーネントiの最初の中央絶対サンプリングモーメントを掛けることをお勧めします。
私のアルゴリズム
考え方は次のとおりです。コンポーネントを破棄し、現在（このコンポーネントなしで）サンプルのセットが線形分離可能かどうかを確認します。 はいの場合、このコンポーネントを返さないでください。返されない場合、返されます。 問題は、線形分離可能性のセットを確認する方法ですか？
xiをサンプル、yiがクラスに属する（yi = -1が最初のクラス、yi = 1が2番目のクラス）i = 1..mとします。 次に、サンプルは次の場合に線形に分離可能です。
-自明ではない解決策があります。
（SVMのトレーニングと同じ条件）。
_____________________________________________________________________________________
最初に、厳密な線形分離性についてセットをチェックする方法を見てみましょう。
-解決策があります。 ファルカシュの補題<=>
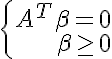
-些細な解決策しかありません。 得られた制約と目的関数を使用して、線形計画問題の最適性についてベクトル0をチェックします。
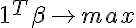
0が最適であることが判明した場合、セットは厳密に線形分離可能です。
_____________________________________________________________________________________
緩やかな線形分離性：
-自明ではない解決策があります。 ファルカシュの補題<=>
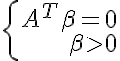
-決定権はありません。 <=>
-決定権はありません。 得られた制約の解を確認するために、これらの制約のある線形計画問題で初期サポートベクトルを見つける方法を使用できます。
_____________________________________________________________________________________
一部の問題（特に次元（n）がサンプル数（m）を超える場合）では、セットの分離が特定のギャップで発生する場合にのみコンポーネントを破棄することがあります。 その後、次の条件を確認できます。
-解決策があり、 c > = 0がギャップパラメータであり、2番目の制限が正規化アルファを置き換えます（そのため、単に十分に大きな定数kを掛けてシステムA * k * x > = cを満たすだけでA * x > 0を解決することは不可能です ）。 Farkashの補題によるこれらの条件（Eは単位行列）<=>
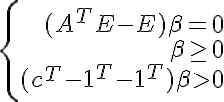
-決定権はありません。 得られた制約（最後の行なし）と目的関数を使用して、線形計画問題の最適性についてベクトル0をチェックします。
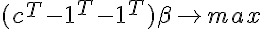
0が最適であることが判明した場合、セットを特定のギャップで分割できます。
_____________________________________________________________________________________
一部の問題（特にサンプル数（m）が次元（n）を超える場合）では、セットの分離が何らかのエラーで発生した場合でもコンポーネントを破棄することがあります。 その後、次の条件を確認できます。
-解があり、 c <= 0がエラーパラメーターであり、2番目の制約が正規化アルファを置き換えます（そのため、解A * x > negative_number_less_than_ cを単純に十分に大きい定数kで除算できず、システムA * x / k> = cを満たすことができます ）。 ここでは、2つの線形計画問題を考慮しなければならない分離（角括弧）のみがあるため、すべてが上記のケースに似ています。