 (c)xkcd
(c)xkcd
複雑な数式とmatlabを使用せずに、次の質問に答えようとします。
- FT、DTF、DTFT-違いは何ですか?完全に異なる一見公式はどのようにそのような概念的に類似した結果を与えるのですか?
- 高速フーリエ変換(FFT)の結果を正しく解釈する方法
- 179サンプルの信号が与えられ、FFTに2のべき乗に等しい長さの入力シーケンスが必要な場合の対処方法
- なぜ、予想される単一の「スティック」ではなく正弦波のフーリエスペクトルを取得しようとすると、奇妙な波線がグラフ上でクロールし、何ができるか
- ADCの前とDACの後にアナログフィルターを配置する理由
- サンプリング周波数の半分より高い周波数でADC信号をデジタル化することは可能ですか(学校の答えは間違っていますが、正しい答えは可能です)
- デジタルシーケンスから元の信号を復元する方法
読者は積分が何であるか、 複素数 ( およびそのモジュールと引数 )、 関数の畳み込みに加えて、少なくとも「指で」 ディラックデルタ関数が何であるかを読者が理解しているという前提から進みます。 わからない-それは重要ではありません、上記のリンクを読んでください。 このテキストの「関数の積」によって、どこでも「点ごとの乗算」を意味します
おそらく、通常のフーリエ変換は、名前が示すように、ある関数を別の関数に変換する、つまり実変数x(t)の各関数をそのスペクトルまたはyのフーリエ変換に関連付ける一種のものであるという事実から始めなければなりません(w):

類推すると、同様の意味の変換の例が微分として機能します。たとえば、関数をその微分に変えることができます。 つまり、フーリエ変換は、本質的には導関数を取得するのと同じ操作であり、多くの場合、同様の方法で示され、関数上に三角形の「キャップ」を描きます。 実数に対して決定できる微分とは対照的に、フーリエ変換は常により一般的な複素数で「機能」します。 このため、複素数は1ではなく、実数で動作するグラフ上の2つの座標によって決定されるため、この変換の結果の表示には常に問題が発生します。 原則として、最も便利な方法は、モジュールと引数の形式で複素数を表し、それらを別々に2つのグラフとして描画することです。
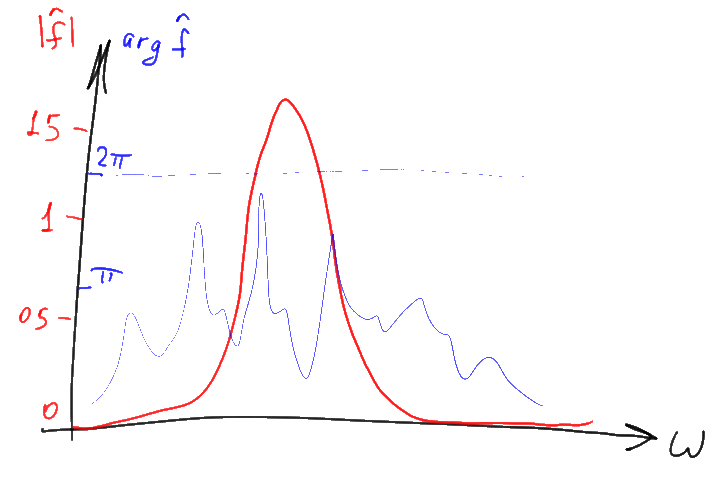
この場合、複素数値の引数のプロットは「位相スペクトル」と呼ばれ、モジュールのグラフは「振幅スペクトル」と呼ばれます。 通常、振幅スペクトルは非常に重要であるため、スペクトルの「位相」部分が見落とされることがよくあります。 この記事では、「振幅」にも焦点を当てますが、グラフの欠落した位相部分の存在を忘れてはなりません。 また、通常の複素数値のモジュールの代わりに、10進数の10倍の10が描画されることが多く、その結果、デシベル(dB)で表示される値の対数グラフが得られます。
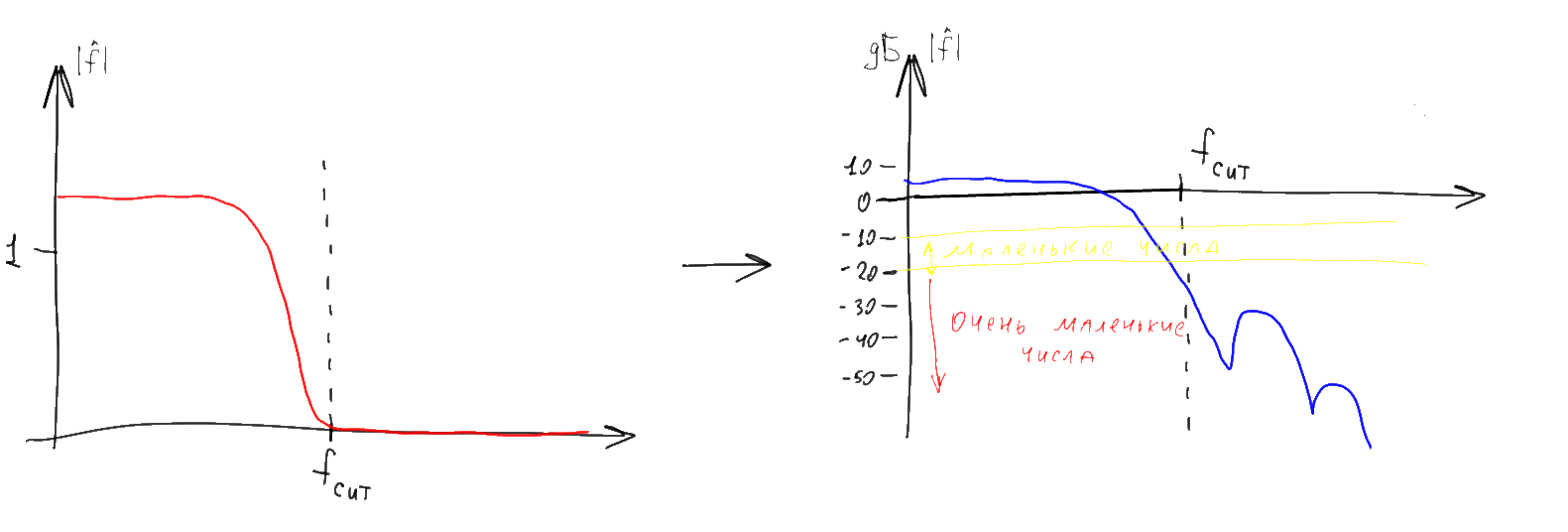
対数グラフの負の数が大きくない(-20 dB以下)ことは、「通常の」グラフではほとんどゼロであることを意味します。 したがって、そのようなグラフのさまざまなスペクトルの長くて広い「尾」は、「通常の」座標で表示されると、原則として事実上消えます。 このような奇妙な一見表現の利便性は、さまざまな関数のフーリエ画像を相互に乗算する必要があることが多いという事実から生じます。 複素数値のフーリエ画像を同様に点ごとに乗算すると、それらの位相スペクトルが加算され、振幅スペクトルが加算されます。 前者は簡単で、後者は比較的難しいです。 ただし、振幅を乗算すると振幅の対数が加算されるため、位相グラフのような対数振幅グラフは単純に点ごとに加算できます。 さらに、実際の問題では、信号の「振幅」ではなく、「パワー」(振幅の2乗)で動作する方が便利な場合がよくあります。 対数目盛では、両方のグラフ(振幅とパワーの両方)は同一に見え、係数のみが異なります。パワーグラフのすべての値は、振幅スケールの2倍です。 したがって、周波数(デシベル単位)で電力分布をプロットするには、何も二乗することはできませんが、10進数の対数を計算し、20を掛けます。
あなたは退屈していますか? 少し待ってください。チャートの解釈方法を説明する記事の退屈な部分で、まもなく終了します:)。 しかし、これの前に、非常に重要なことを理解する必要があります:上記のスペクトルのグラフは、限られた値の範囲(特に、正の数)で描かれていますが、これらのグラフはすべて実際にはプラスとマイナスの無限に続きます。 グラフは単にグラフの「最も意味のある」部分を表します。これは通常、負のパラメーター値にミラーリングされ、より大きなスケールで検討すると、いくつかのステップで定期的に繰り返されることがよくあります。
グラフに何を描画するかを決定したら、フーリエ変換自体とそのプロパティに戻りましょう。 この変換を決定するにはいくつかの異なる方法がありますが、詳細は異なります(異なる正規化)。 たとえば、私たちの大学では、何らかの理由で、フーリエ変換の正規化を使用することが多く、角周波数(ラジアン/秒)の観点からスペクトルを決定します。 通常の周波数(ヘルツ)の観点からスペクトルを定義する、より便利な西洋式を使用します。 この場合の直接および逆フーリエ変換は左側の式によって決定され、必要なこの変換のいくつかのプロパティは右側の7つの項目のリストによって決定されます。
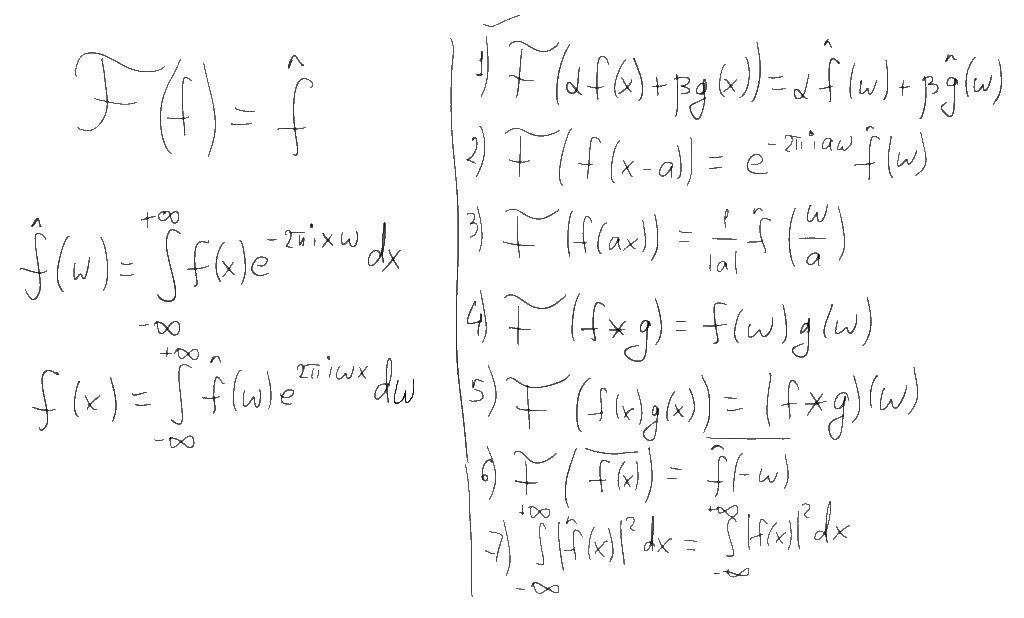
これらのプロパティの最初は線形性です。 関数の線形結合をとると、この結合のフーリエ変換は、これらの関数のフーリエ画像の線形結合になります。 この特性により、複雑な関数とそのフーリエ変換をより単純な関数に減らすことができます。 たとえば、周波数fおよび振幅aの正弦関数のフーリエ変換は、ポイントfおよび-fに位置し、係数a / 2の2つのデルタ関数の組み合わせです。

異なる周波数の正弦波の集合の合計で構成される関数を使用する場合、線形性に従って、この関数のフーリエ画像は対応するデルタ関数の集合で構成されます。 これにより、「振幅aが関数のスペクトルの周波数fに対応する場合、元の関数は正弦波の合計として表すことができ、そのうちの1つは周波数fと振幅2aの正弦波である」という原則に従って、スペクトルを単純に視覚的に解釈できます。 厳密に言えば、デルタ関数とグラフ上の点は完全に異なるものであるため、この解釈は正しくありませんが、後で見るように、離散フーリエ変換では真実からそれほど遠くありません。
フーリエ変換の2番目の特性は、信号の時間シフトからの振幅スペクトルの独立性です。 関数をx軸に沿って左右に移動すると、その位相スペクトルのみが変化します。
3番目のプロパティは、時間軸(x)に沿った元の関数の拡張(圧縮)であり、周波数スケール(w)でそのフーリエイメージを比例的に圧縮(ストレッチ)します。 特に、有限の持続時間の信号のスペクトルは常に無限に広く、逆の場合、有限の幅のスペクトルは常に無制限の持続時間の信号に対応します。
4番目と5番目のプロパティは、おそらく最も有用です。 関数の畳み込みをフーリエ画像の点ごとの乗算に、またはその逆に-関数のフーリエ画像の畳み込みへの点ごとの乗算を減らすことができます。 もう少し詳しく説明します。
6番目の特性は、フーリエ画像の対称性について述べています。 特に、この特性から、実数値関数(つまり、「実」信号)のフーリエ変換では、振幅スペクトルは常に偶数関数であり、位相スペクトル(範囲-pi ... piに移動した場合)は奇数です。 。 このため、スペクトルの負の部分はほとんどスペクトルグラフにプロットされません。実数値の信号の場合、新しい情報は提供されません(ただし、ゼロではありません)。
最後に、最後の7番目の特性は、フーリエ変換が信号の「エネルギー」を保存することを示唆しています。 これは、エネルギーが有限である有限持続時間の信号に対してのみ意味があり、無限大でのそのような信号のスペクトルはすぐにゼロに近づくことを示唆しています。 この特性により、原則として、エネルギーの大部分を運ぶ信号の「主要な」部分のみが通常スペクトルグラフに描かれます-グラフの残りの部分は単純にゼロになります(ただし、再びゼロではありません)。
これらの7つのプロパティを使用して、信号の「デジタル化」の数学を見てみましょう。これにより、連続信号を一連の数値に変換できます。 これを行うには、「Dirac comb」と呼ばれる機能を使用する必要があります。
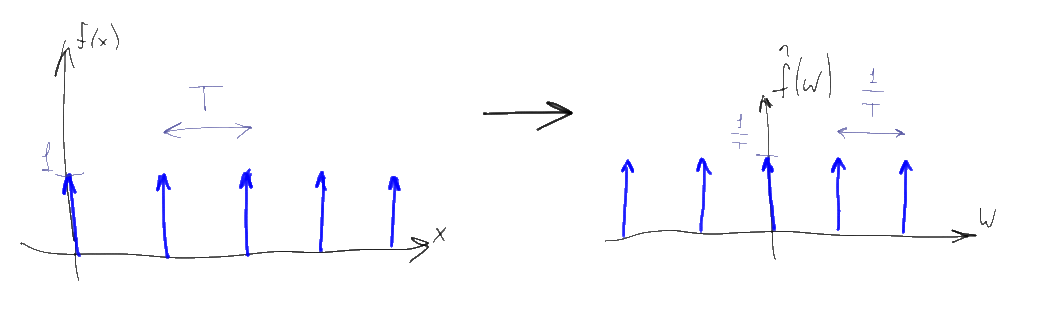
ディラックコームは、ゼロから始まりステップTで始まる単位係数を持つデルタ関数の周期的なシーケンスです。信号をデジタル化するには、Tをできるだけ小さく、T << 1を選択します。 この関数のフーリエ画像もディラックコームであり、非常に大きな1 / Tステップとわずかに低い係数(1 / T)しかありません。 数学的な観点から見ると、信号の時間による離散化は、単に元の信号にディラックの櫛を点ごとに乗算することです。 値1 / Tは、サンプリング周波数と呼ばれます。
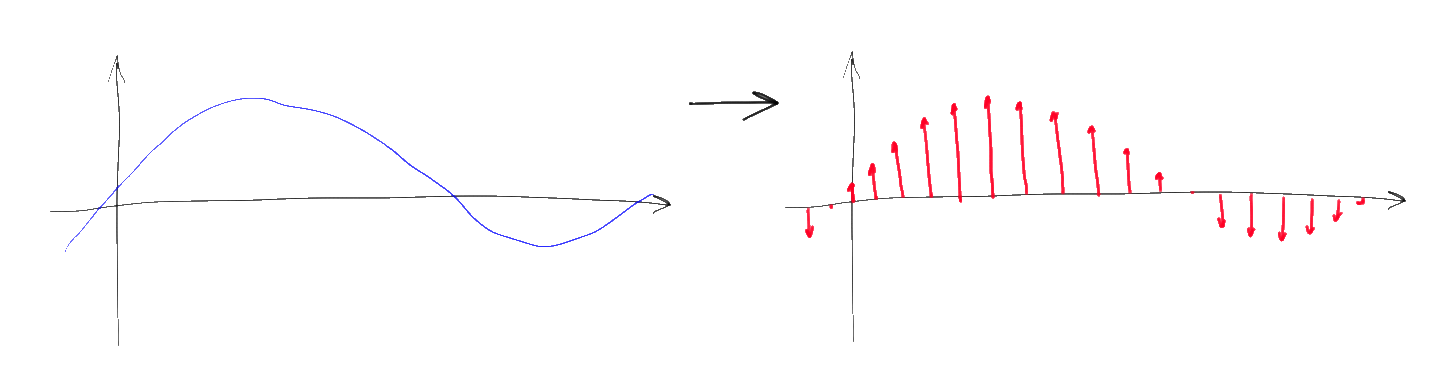
連続関数の代わりに、そのような乗算の後、特定の高さの一連のデルタパルスが取得されます。 さらに、フーリエ変換の特性5によると、結果として得られる離散信号のスペクトルは、元のスペクトルと対応するディラックコームの畳み込みです。 畳み込みの特性に基づいて、元の信号のスペクトルは、周波数軸に沿って1 / Tの増分で無限に「コピー」され、合計されることは容易に理解できます。
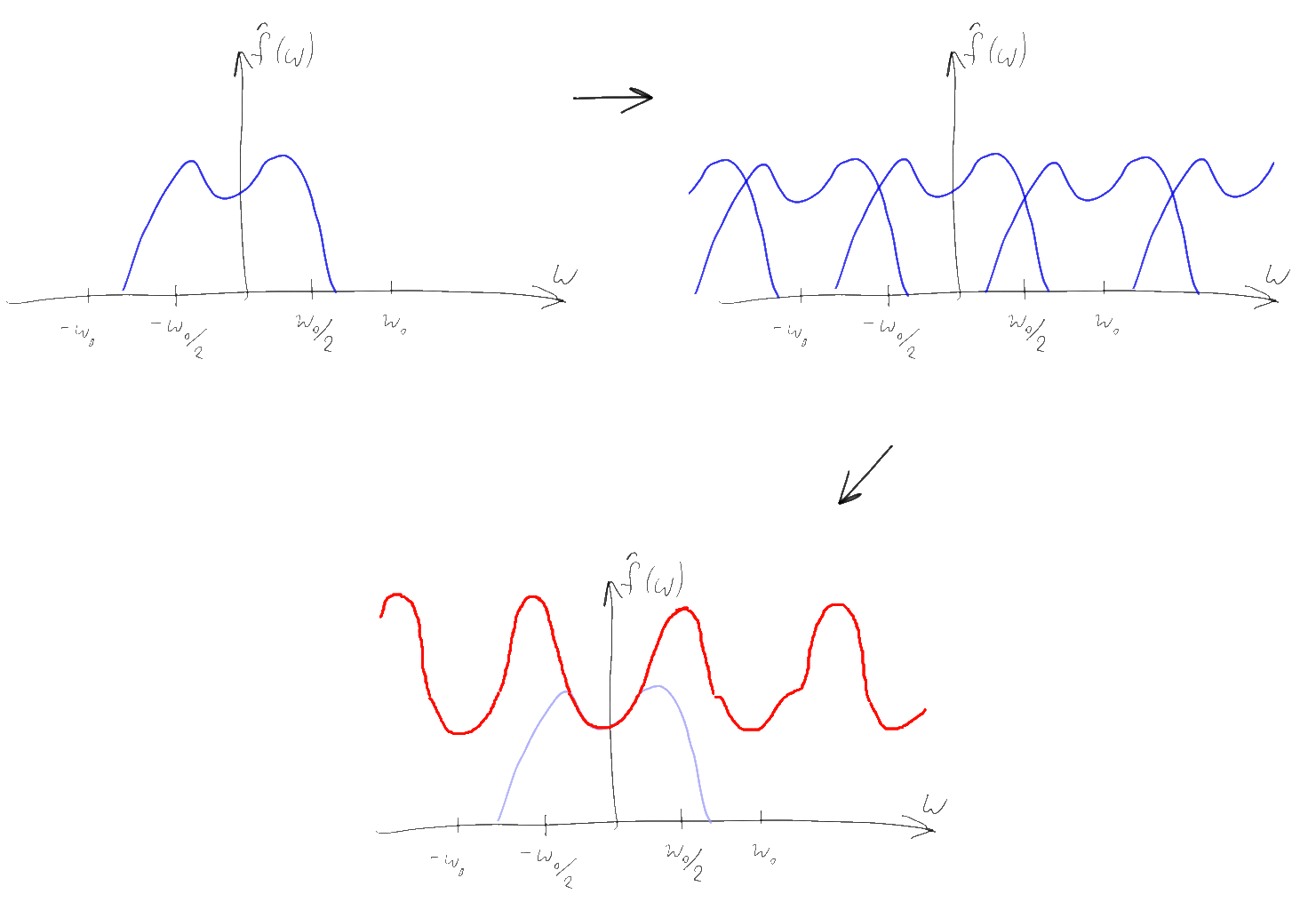
元のスペクトルの幅が有限であり、十分に大きいサンプリング周波数を使用した場合、元のスペクトルのコピーは重複しないため、一緒に加算されないことに注意してください。 このような「崩壊した」スペクトルから元のスペクトルを復元するのは簡単であることを理解するのは簡単です-ゼロの領域のスペクトル成分を取り、無限に行く余分なコピーを「切断」するだけで十分です。 これを行う最も簡単な方法は、-1 / 2T ... 1 / 2Tの範囲でTに等しく、この範囲外のゼロに等しい矩形関数をスペクトルに乗算することです。 同様のフーリエ変換は関数sinc (Tx)に対応し、プロパティ4によると、このような乗算はデルタ関数の元のシーケンスと関数sinc(Tx)の畳み込みに相当します。
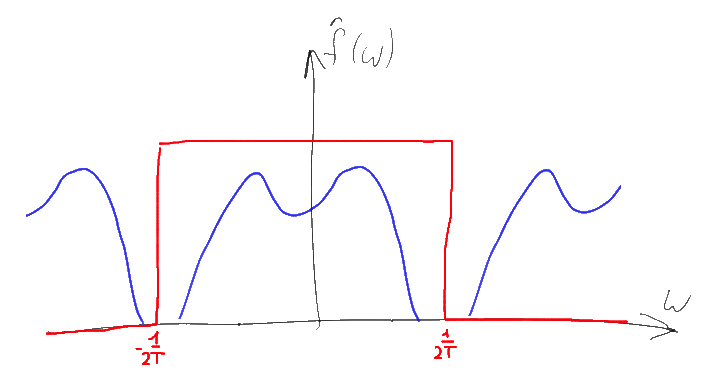

つまり、フーリエ変換を使用すると、元の信号に存在する最大周波数を超える少なくとも2倍のサンプリング周波数(スペクトルに負の周波数が存在するため)を使用するという条件下で、時間離散化された信号から元の信号を簡単に復元する方法が得られました。 この結果は広く知られており、 「コテルニコフ/シャノン-ナイキストの定理」と呼ばれています。 しかし、今では(証拠を理解して)簡単に気付くので、この結果は、誤解が広まっているのとは反対に、元の信号を復元するのに十分ではあるが必要ではない条件を決定します。 必要なのは、信号をサンプリングした後、関心のあるスペクトルの一部が重ならないことを確認することです。信号が十分に狭帯域である場合(スペクトルの非ゼロ部分の小さな「幅」がある場合)信号の最大周波数の2倍以上。 同様の手法は「アンダーサンプリング」 (サブサンプリング、 帯域サンプリング )と呼ばれ、あらゆる種類の無線信号の処理に広く使用されています。 たとえば、88〜108 MHzの周波数帯域で動作するFMラジオを使用する場合、コテルニコフの定理で想定される216 MHzではなく、43.5 MHzの周波数のADCを使用してデジタル化できます。 ただし、この場合、高品質のADCと優れたフィルターが必要です。
高次の周波数と低次の周波数(エイリアス)の「重複」は、信号サンプリングの直接的な性質であり、結果を不可逆的に「損なう」ことに注意してください。 したがって、原則として信号に高周波周波数が含まれる場合(つまり、ほとんどの場合)、アナログフィルターがADCの前に配置され、元の信号では不要なものはすべて直接「カットオフ」されます(サンプリング後にこれを行うには遅すぎるため)。 アナログデバイスとしてのこれらのフィルターの特性は不完全であるため、信号の「スポイリング」が依然として発生し、実際には、スペクトルの最高周波数は原則として信頼できません。 この問題を軽減するために、入力アナログフィルターをより低い通過帯域に配置し、ADCの理論的に利用可能な周波数範囲の低い部分のみを使用しながら、信号を過大評価のサンプリングレートでサンプリングすることがよくあります。
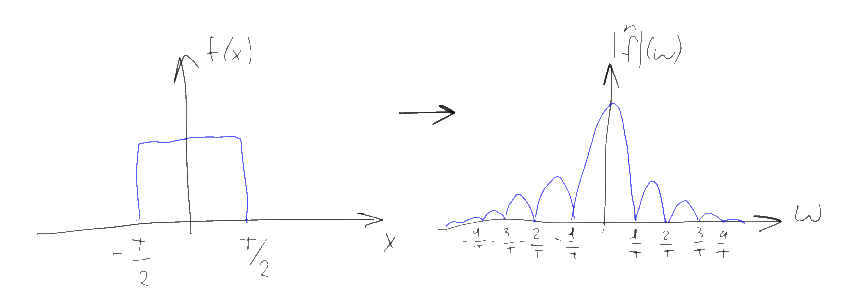
ちなみに、もう1つのよくある誤解は、DACの出力の信号が「ステップ」で描画されることです。 「ステップ」は、幅Tおよび高さ1の矩形関数を使用した、サンプリングされた信号シーケンスの畳み込みに対応します。
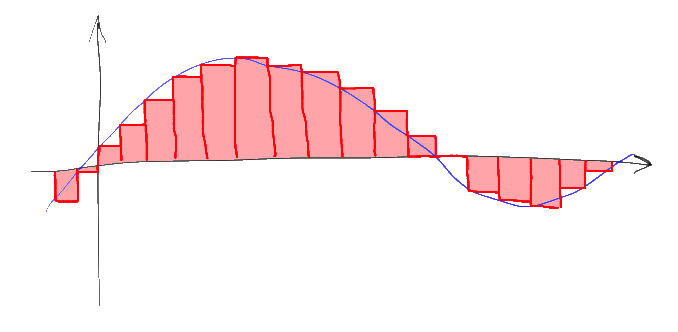
この変換中の信号のスペクトルは、この長方形関数のフーリエ変換で乗算されます。同様の長方形関数では、sinc(w)であり、強いほど「ストレッチ」され、対応する長方形の幅が小さくなります。 同様の「DAC」でサンプリングされた信号のスペクトルには、このスペクトルが点ごとに乗算されます。 さらに、スペクトルの「余分なコピー」を伴う不必要な高周波は完全にはカットされず、逆にスペクトルの「有用な」部分の上部は弱められます。
もちろん、実際には誰もしません。 DACの構築にはさまざまなアプローチがありますが、意味が最も近い計量タイプのDACでさえ、逆にDACの矩形パルスは、スペクトルの有用な部分を不必要に抑制することを避けるために、可能な限り短く選択されます(実際のデルタ関数のシーケンスに近づく)。 結果として生じる広帯域信号の「過剰な」周波数は、アナログローパスフィルターに信号を通すことによってほぼ常に抑制されるため、コンバーターの「内部」にも、その出力にも「デジタルステップ」はありません。
ただし、フーリエ変換に戻ります。 事前にサンプリングされた信号シーケンスに適用される上記のフーリエ変換は、離散時間フーリエ変換(DTFT)と呼ばれます。 このような変換によって得られるスペクトルは常に1 / T周期的です;したがって、DTFTスペクトルは区間[0 ... 1 / T)の値によって完全に決定されるため、DTFTスペクトルはこの区間に制限されることがよくあります。 さらに、DTFTの結果は、サンプリングされた信号のスペクトルであるという事実にもかかわらず、依然として「アナログ」機能です。 さらに、「通常の」実数値信号の場合、このスペクトルの後半は、特性6により、ナイキスト周波数1/2 Tに対して反射される左半分を反映します。
これまで、マイナスからプラスの無限大まで定義された信号が変換の入力に到達すると仮定しました。 ただし、利用可能な実際の信号の長さは常に有限です。どうすればよいですか? FTおよびDTFTでこの問題を解決するために、最終信号には左右に無限にゼロが埋め込まれます。 元の信号が元々有限であり(これが別のインパルスである場合)、それが完全にフーリエ変換に該当する場合、このアプローチは望ましい結果を直接与えます。 ただし、多くの場合、フーリエ変換に使用される「最終」信号は、実際には、たとえば正弦波など、より長く、場合によっては無限の信号の一部です。 この場合、ゼロを含む最終セグメントの追加は次のように解釈されます。元の信号の長さは無限に長いと考えられますが、その後、重み関数が掛けられます。測定に使用できるセグメントの外側に消える「ウィンドウ」です。 最も単純な場合、「ウィンドウ」の役割は、左右の最終信号に無限のゼロを追加するだけであるという事実に対応する、単なる長方形の機能によって果たされます。 より複雑なものでは、最初のシーケンスに「ウィンドウ」関数によって決定された重みが乗算され、再びゼロが追加されます。
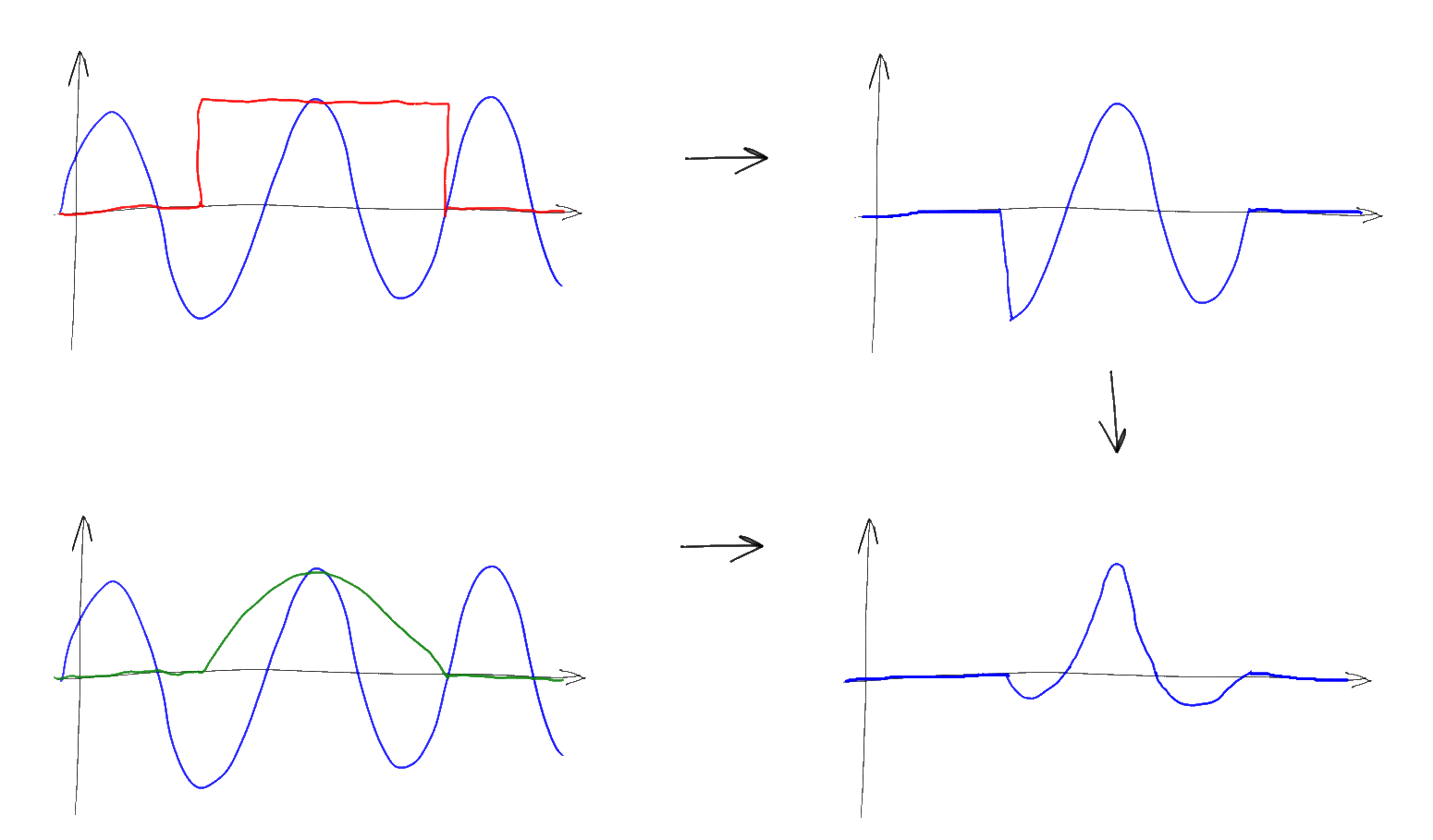
既におなじみのプロパティ5を使用すると、このような乗算では、初期信号が窓関数のスペクトルで単純に崩壊することが簡単にわかります。 たとえば、正弦波(デルタ関数)のスペクトルを測定しようとして、測定間隔を長方形のウィンドウに制限すると、デルタ関数の代わりに結果のスペクトルにウィンドウのスペクトルが表示されます-つまり Tsinc(T(xf)):

この場合、Tは信号を制限する間隔の長さであるため、入力信号が長くなるほど、観測されるスペクトルが真のデルタ関数に近くなります。 メインローブの最終的な「幅」は、周波数が互いに近いソース信号の正弦波の存在を確実に区別することを不可能にし、「サイドローブ」の存在は、離れた周波数に小さな歪みを導入し、特にスペクトルを測定する必要がある場合、個々の周波数の振幅を正確に測定することを困難にしますスペクトル内の1桁のより強力な成分の存在下での小振幅の領域。 この効果は「スペクトル漏れ」と呼ばれ、無限の信号に対して完全に無効にすることはできませんが、信号が測定される間隔が長くなるほど、この漏れの影響は小さくなります。 ウィンドウ関数を選択することで、メイン周波数付近にスペクトルを集中させることで(このスペクトルを強く「ぼかす」が、隣接する周波数に干渉しない)、またはどこにでも拡散させる(ピークのぼけは減少するが「ノイズ」は増加し、その結果、このリークの「幅」を制御できます-個々の周波数の振幅の測定誤差)。スペクトル漏れで選択されたサンプリング周波数はほとんど役割を果たさないことに注意してください-短い信号スパンは少なくとも10 GHzでサンプリングできますが、これは測定可能な周波数の数を増やすだけですが、個々の周波数を決定する精度は依然として低いままです。
興味深い特別なケースは、離散周波数nFのセットを持つ信号が周波数mFでサンプリングされる状況です。ここで、m、nは整数です。この場合、「ウィンドウ」のゼロとスペクトル内のデルタ関数の位置は正確に一致し、周波数はまだ「不鮮明」ですが、ポイントmFでの振幅は真の振幅と一致します。「ノイズ」はゼロです。この性質により、離散フーリエ変換のコテルニコフ定理の類似物を証明することができますが、実際には、そのような信号は残念ながら実際には発生しません。
そこで、「入力」を計算しました。無限長の連続関数から、有限数の離散サンプルを取得して処理することができ、その代わりにスペクトルの幅と周波数漏れの制限がありました。ただし、「終了」DTFTは依然として継続的な機能であり、コンピューターでの作業は困難です。実際には、この問題は非常に簡単に解決されます-完全なセグメント[0,1 / T)はk個の等しい部分に分割され、DTFTは点fi = i / kT(i = 0,1、... k-1)で考慮されます結果の構造は、「離散フーリエ変換」(DFT)と呼ばれます。

Tと「ウィンドウ」の選択に関連する質問からTを削除することにより、最後の変換を正規化すると便利です。この正規化された表記は、N複素数のシーケンス変換としてのDFTの定義としてよく使用されます。

この形式で記述されたフーリエ変換の美しさは、DTFTのすべての利点を保持しながら、「スムーズ」 kの同様のDTF (たとえば、2のべき乗)をk log(k)のオーダーで非常に迅速に計算できることです。対応するアルゴリズムは「高速フーリエ変換」(FFT)と呼ばれ、一般的にはいくつかあります。ただし、実用的な観点からは、それらはすべて「ブラックボックス」と見なすことができ、入力で一連の複素数を受け取り、出力で一連の複素数を発行します。したがって、有限長のサンプリングされた信号を使用すると、この信号に最初に適切な重み関数が乗算され、次に右側に必要な数のゼロが追加され、FFTアルゴリズムに渡されます。
結果を解釈する方法は?上記を考慮して、
- 結果の値は、DTFTスペクトル上のサンプルの均一なグリッドです。読み取り値が多いほど、グリッドが細かくなり、スペクトルがより目立ちます。既知のシーケンスにゼロの望ましい数を追加すると、連続スペクトルに任意に近い近似を計算できます
- DTFTスペクトルは、0〜1 / T(1 / Tはサンプリング周波数)の周波数間隔で指定され、この間隔の外側で無限に定期的に繰り返されます。
- このスペクトルは、複素数(実数のペア)で与えられます。振幅は複素数のモジュラス、位相は引数として定義されます。
- 有効な入力信号の場合、1 / 2T ... 1 / T範囲のスペクトルは、0 ... 1 / 2Tスペクトルを単純にミラーリングし、それに応じてペイロードを搬送しません(単にスペクトルを切断してスペクトルを視覚化できます)
- , ( ) —
- “ ” “ ”. ( !) — .
- . , , , , k/T.
- A ( ) A*N/2, , “” “” A*N, 1/2T ( A*N, , ). N = T1/T0, T1 — ( «»), T0 — ( ) , , ( )
まあ、それがすべてです。フーリエ変換とFFTアルゴリズムがシンプルでわかりやすく、使いやすいツールになることを願っています。