ブルームフィルターの誤検知の数。
説明
Bloom Filterは、1970年にBurton Bloomによって開発されたランダム化されたクエリデータ構造です。 ブルームフィルターは、リクエストに対する誤った応答、いわゆる 誤検知操作。 つまり 要素を追加すると、ブルームフィルターが要素がベクトルに含まれているという回答を返す可能性がゼロではありませんが、存在しません。
大まかに言えば、ブルームフィルターは2つの可能な答えを返します。
- ベクトルに要素がありません
- 要素はおそらくベクトル内にあります
ブルームはそのような誤った答えの可能性を分析しましたが、彼の分析は間違っています。
ブルームフィルターの構成については説明しませんが、これについては、対応するブルームフィルターの記事またはWIKI Wikiで読むことができます:ブルームフィルター
はじめに
ブルームフィルターは、 n個の要素のセットSをビットベクトルにマッピングするデータ構造です
 。 要素を記述するために、 k-ランダムハッシュ関数が使用されます。
。 要素を記述するために、 k-ランダムハッシュ関数が使用されます。  。 最初に、ベクトルはゼロに初期化されます。 要素は、ベクトルBのすべてのkビットを1に設定することによって記録されます。
。 最初に、ベクトルはゼロに初期化されます。 要素は、ベクトルBのすべてのkビットを1に設定することによって記録されます。 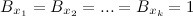 。 要素の存在を確認するには
。 要素の存在を確認するには 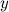 フィルタでは、ベクトルの各kビットの値を見つけるだけで十分です。 少なくとも1つのゼロがある場合、これはベクトルにそのような要素がまだないことを意味し、すべてのビットが1に設定されている場合、これはおそらくその要素がすでに存在することを示します。 この状況は誤検知と呼ばれます。
フィルタでは、ベクトルの各kビットの値を見つけるだけで十分です。 少なくとも1つのゼロがある場合、これはベクトルにそのような要素がまだないことを意味し、すべてのビットが1に設定されている場合、これはおそらくその要素がすでに存在することを示します。 この状況は誤検知と呼ばれます。
Bloomは、以下のように誤検知をカウントしました。
ベクトルBの任意のビットがゼロである確率は
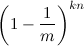 n個の要素を追加するときにk個のハッシュ関数のすべての単位を設定した後。
n個の要素を追加するときにk個のハッシュ関数のすべての単位を設定した後。
したがって、特定のビットが1に設定される確率は

さあ、持ってきて
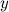 偽陽性、ベクトルの各kビット
偽陽性、ベクトルの各kビット  1に設定する必要があります。 これの確率:
1に設定する必要があります。 これの確率:
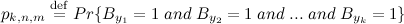
等しいと主張されている

何年も前に現れたこの証拠は間違っています。 エラーは、イベントが暗黙的に仮定されているという事実にあります
 とイベント
とイベント 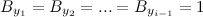 独立していると見なされます。 一見したところ、これは本当のようです。
独立していると見なされます。 一見したところ、これは本当のようです。  独立しています。 ただし、ケースを考慮することにより、証明に対する単純な反例が得られます。
独立しています。 ただし、ケースを考慮することにより、証明に対する単純な反例が得られます。 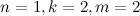 。 この場合、16の可能な状況の単純な列挙により、誤検知操作の確率が5/8であることが明らかになり、ブルーム式では結果として9/16 = 4.5 / 8が得られます。
。 この場合、16の可能な状況の単純な列挙により、誤検知操作の確率が5/8であることが明らかになり、ブルーム式では結果として9/16 = 4.5 / 8が得られます。
正確な式
ボールとバスケットの問題として誤検知の数を決定する問題をシミュレートします。 m-バスケットがあります。 私たちはknの白いボールをランダムなバスケットに投げます。 バスケットに少なくとも1つの白いボールが含まれている場合、バスケットを白と見なすことができます。 次に、 k- blackボールをバスケットに入れます。 イベントAで、各黒いボールが白いバスケットに置かれているとします。 このイベントの確率を計算します。
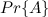 。
。
多くの白いバスケットはサブセットとして表すことができることに注意してください
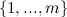 。 いずれかの
。 いずれかの 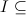
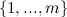 示す
示す 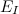 私が多数の白いバスケットであるというイベントとして。 等しいパワー
私が多数の白いバスケットであるというイベントとして。 等しいパワー 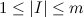 。 条件付き確率式を使用します。
。 条件付き確率式を使用します。
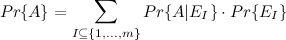
私が固定されている場合、
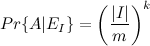
どこで
 それ自体に含まれています
それ自体に含まれています
- サイズknのセットから値iのセットへのマッピングの数
- サイズknのセットからサイズmのセットまでの関数の数
サイズknのセットからサイズiのセットへのマッピングの数は、式
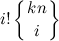 どこで
どこで
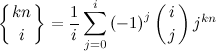
サイズknのセットからサイズmのセットまでの関数の数は
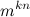 。
。
次の式を組み合わせます。
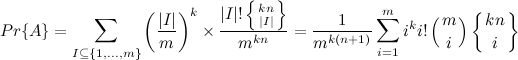
最終結果
その結果、 kハッシュ関数を使用してn個の要素を追加するときのmビットのブルームフィルターの誤検出の確率は次のようになります。

この式は、元々ブルームが計算したほど単純ではありません。 さらに詳しく説明することなく、この記事の著者はこの式の上限と下限についても説明し、ブルームが推定した最初の式は下限としてのみ使用できるという結論に達します。
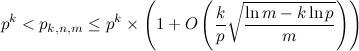
元の記事のテキスト:
ブルームフィルターの偽陽性率について