 こんにちは この記事では、勾配降下法を使用して データをクラスタリングする方法について説明します。 正直なところ、この方法は実用的というよりも本質的に学術的です。 同じ方法をさまざまな方法で解決する方法を示すために、機械学習コースのデモンストレーション目的でこのメソッドを実装する必要がありました。 もちろん、特定のデータセットの勾配を計算するよりも重心を見つけるのが計算上困難な微分可能なメトリックを使用してデータをクラスター化する場合は、この方法が役立ちます。 したがって、勾配降下法を使用して一般化されたメトリックでk-meansクラスタリング問題を解決する方法に興味がある場合は、catの下で質問します。 Rのコード
こんにちは この記事では、勾配降下法を使用して データをクラスタリングする方法について説明します。 正直なところ、この方法は実用的というよりも本質的に学術的です。 同じ方法をさまざまな方法で解決する方法を示すために、機械学習コースのデモンストレーション目的でこのメソッドを実装する必要がありました。 もちろん、特定のデータセットの勾配を計算するよりも重心を見つけるのが計算上困難な微分可能なメトリックを使用してデータをクラスター化する場合は、この方法が役立ちます。 したがって、勾配降下法を使用して一般化されたメトリックでk-meansクラスタリング問題を解決する方法に興味がある場合は、catの下で質問します。 Rのコード
データ
まず、アルゴリズムをテストする多くのデータについて説明しましょう。 テストのために、 スマートフォンのセンサーからの多くのデータが使用されます :7352の観測で合計563フィールド。 下から2つのフィールドは、ユーザーIDとアクションのタイプが強調表示されています。 センサーの測定値に応じてユーザーアクションを分類するために、合計6つのアクション(WALKING、WALKING_UPSTAIRS、WALKING_DOWNSTAIRS、SITTING、STANDING、LAYING)の合計が作成されました。 上記のリンクでセットのより詳細な説明を見つけることができます。
理解できるように、寸法を減らすことなくそのようなセットを視覚化することは少し問題です。 ディメンションを縮小するために、 主成分メソッドが使用されました。このために、標準のR言語ツールを使用するか、リポジトリから同じ言語でこのメソッドを実装できます 。 最初と3番目のメインコンポーネントに投影された元のセットがどのように見えるかを見てみましょう。
コード
m.proj <- ProjectData(m.raw, e$eigenVectors[, c(1, 3)]) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(6)[unclass(as.factor(samsungData$activity))], xlab="first", ylab="third", main="Two components; actions")
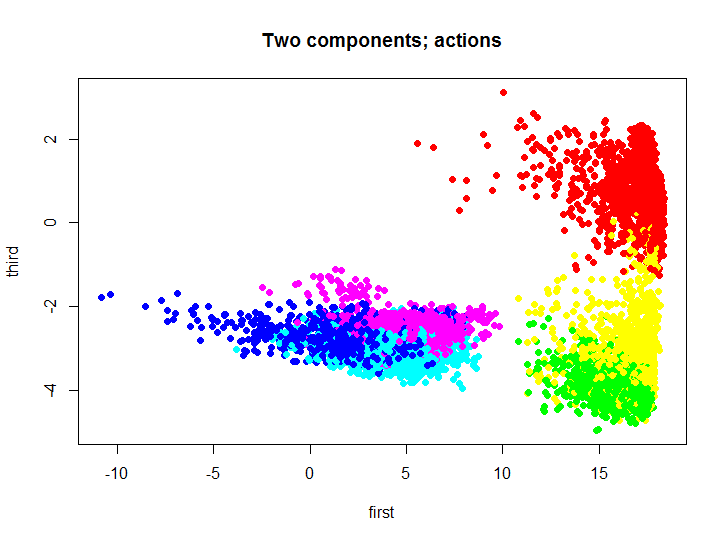
異なる色は異なるアクションを表します。次に、この2次元セットを使用して、クラスタリングの結果をテストおよび視覚化します。
K平均アルゴリズムコスト関数
次の表記法を紹介します。
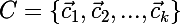 -多くの重心
-多くの重心 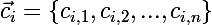 それぞれのクラスター
それぞれのクラスター  -クラスター化される元のデータセット
-クラスター化される元のデータセット 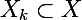 k番目のクラスターは、元のセットのサブセットです
k番目のクラスターは、元のセットのサブセットです
次に、 古典的なk-meansアルゴリズムのコスト関数を考えます 。
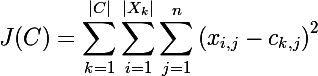
つまり このアルゴリズムは、重心からのクラスター要素の二次偏差の合計を最小化します。 言い換えると、対応する重心からのクラスター要素のユークリッド距離の平方和が最小化されます。
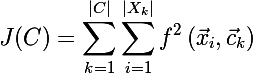 、ここでf-この場合はユークリッド距離です。
、ここでf-この場合はユークリッド距離です。
ご存知のように、この問題を解決するために、期待値最大化アルゴリズムに基づいた効果的な学習アルゴリズムがあります 。 Rに組み込まれた関数を使用して、このアルゴリズムの結果を見てみましょう。
コード
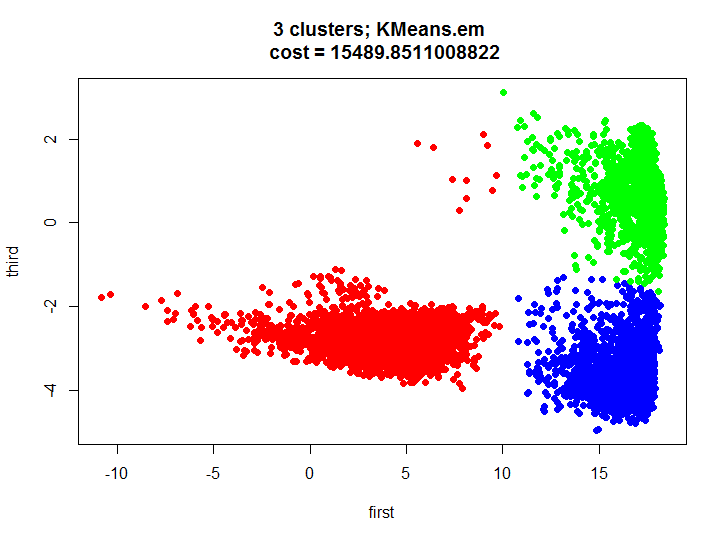
kmeans.inner <- kmeans(m.proj, 3) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(3)[unclass(as.factor(kmeans.inner$cluster))], xlab="first", ylab="third", main=paste(k, " clusters; kmeans \n cost = ", kmeans.inner$tot.withinss/2, sep=""))
勾配降下
勾配降下アルゴリズム自体は非常に単純で、最終的には勾配方向とは反対の方向に小さなステップで移動します。たとえば、誤差逆伝播アルゴリズムが機能するか、限定的なボルツマンマシンをトレーニングするための対比発散アルゴリズムです 。 まず、目的関数の勾配、またはモデルパラメーターに関する目的関数の偏微分を計算する必要があります。
 、古典的なk-meansに関するセクションを残したので、 fは、原則として、必ずしもユークリッドメトリックではなく、距離の任意の尺度になります
、古典的なk-meansに関するセクションを残したので、 fは、原則として、必ずしもユークリッドメトリックではなく、距離の任意の尺度になります
ただし、問題があります。この段階では、集合Xのクラスターへのパーティションが何であるかはわかりません。 目的関数を再定式化して、簡単に区別できる単一の式の形式で記述します。セットの各要素から3つの重心の1つまでの最小距離の合計です。 この式は次のとおりです。
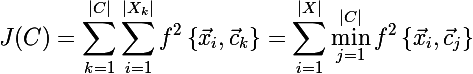
次に、新しい目的関数の導関数を見つけましょう。
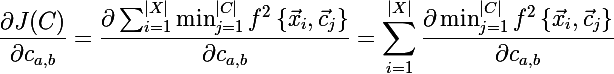
さて、最小導関数が何であるかを見つけることは残っていますが、すべてが単純であることが判明します: a重心が実際にセットの現在の要素からの距離が最小になるものである場合、式の導関数はベクトル要素に関する距離の2乗の導関数に等しくなります。ケースはゼロです:

メソッドの実装
ご理解のとおり、前の段落のすべての手順は、距離を二乗することなく実行できます。 これは、このメソッドを実装するときに行われました。 このメソッドは、2番目のベクトルの成分に関する距離関数と2つのベクトル間の距離関数の偏微分の計算関数をパラメーターとして受け取ります。たとえば、「ユークリッド距離の半分の半分」(微分が非常に単純なので使用に便利です)、および勾配降下関数自体:
距離関数
距離関数
偏微分関数
HalfSqEuclidian.distance <- function(u, v) { # Half of Squeared of Euclidian distance between two vectors # # Args: # u: first vector # v: second vector # # Returns: # value of distance return(sum((uv)*(uv))/2) }
偏微分関数
HalfSqEuclidian.derivative <- function(u, v, i) { # Partial derivative of Half of Squeared of Euclidian distance # between two vectors # # Args: # u: first vector # v: second vector # i: index of part of second vector # # Returns: # value of derivative of the distance return(v[i] - u[i]) }
勾配降下法
KMeans.gd <- function(k, data, distance, derivative, accuracy = 0.1, maxIterations = 1000, learningRate = 1, initialCentroids = NULL, showLog = F) { # Gradient descent version of kmeans clustering algorithm # # Args: # k: number of clusters # data: data frame or matrix (rows are observations) # distance: cost function / metrics # centroid: centroid function of data # accuracy: accuracy of calculation # learningRate: learning rate # initialCentroids: initizalization of centroids # showLog: show log n <- dim(data)[2] c <- initialCentroids InitNewCentroid <- function(m) { c <- data[sample(1:dim(data)[1], m), ] } if(is.null(initialCentroids)) { c <- InitNewCentroid(k) } costVec <- vector() cost <- NA d <- NA lastCost <- Inf for(iter in 1:maxIterations) { g <- matrix(rep(NA, n*k), nrow=k, ncol=n) #calculate distances between centroids and data d <- matrix(rep(NA, k*dim(data)[1]), nrow=k, ncol=dim(data)[1]) for(i in 1:k) { d[i, ] <- apply(data, 1, FUN = function(v) {distance(v, c[i, ])}) } #calculate cost cost <- 0 for(i in 1:dim(data)[1]) { cost <- cost + min(d[, i]) } if(showLog) { print(paste("Iter: ", iter,"; Cost = ", cost, sep="")) } costVec <- append(costVec, cost) #stop conditions if(abs(lastCost - cost) < accuracy) { break } lastCost <- cost #calculate gradients for(a in 1:k) { for(b in 1:n) { g[a, b] <- 0 for(i in 1:dim(data)[1]) { if(min(d[, i]) == d[a, i]) { g[a, b] <- g[a, b] + derivative(data[i, ], c[a, ], b) } } } } #update centroids for(a in 1:k) { for(b in 1:n) { c[a, b] <- c[a, b] - learningRate*g[a, b]/dim(data)[1] } } } labels <- rep(NA, dim(data)[1]) for(i in 1:dim(data)[1]) { labels[i] <- which(d[, i] == min(d[, i])) } return(list( labels = labels, cost = costVec )) }
テスト中
KMeans.gd.result <- KMeans.gd(k, m.proj, HalfSqEuclidian.distance, HalfSqEuclidian.derivative, showLog = T) plot(m.proj[, 1], m.proj[, 2], pch=19, col=rainbow(k)[unclass(as.factor(KMeans.gd.result$labels))], xlab="first", ylab="third", main=paste(k, " clusters; KMeans.gd \n cost = ", KMeans.gd.result$cost[length(KMeans.gd.result$cost)], sep=""))
クラスタリングの結果を見て、ほぼ同一であることを確認しましょう。
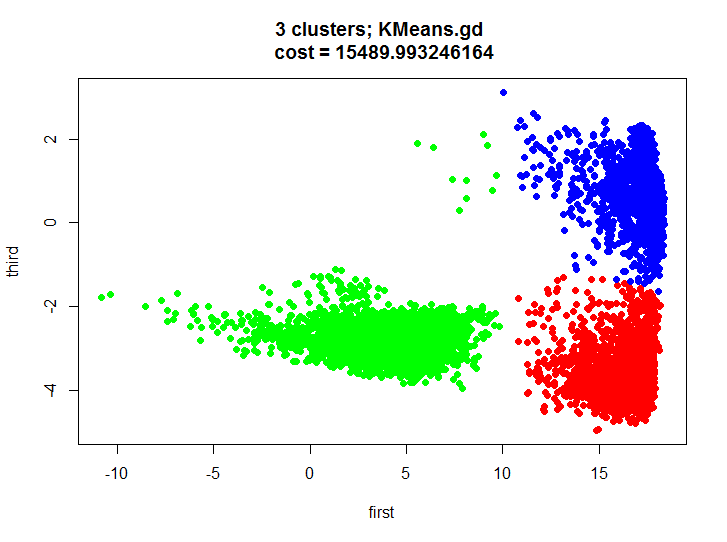
そして、両方のアルゴリズムの反復からのコスト関数の値のダイナミクスのように見えます:
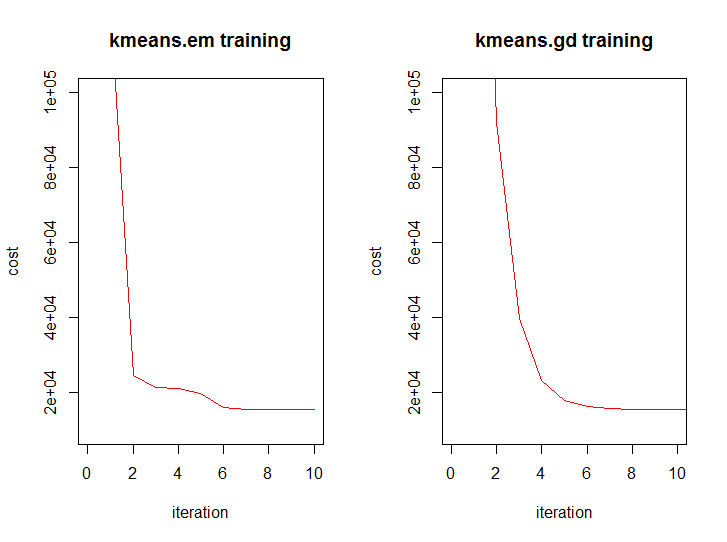
おわりに
最初に、テストで何が起こったのかを少し説明しましょう。 2次元セットを3つのクラスターに適切に分割し、クラスターがあまり重なり合わないことを視覚的に確認し、各クラスターのアクションを認識するためのモデルを完全に構築して、ハイブリッドモデルを得ることができます(1つのクラスターには主に1つのアクション、他の2つ、 3)。
ユークリッド距離を使用したクラスタリングのアルゴリズムの複雑さを見てみましょう。1回の反復のみを考慮します(反復回数の分析は決して簡単な作業ではありません)。 kをクラスターの数、nをデータの次元、mをデータの量(k <= m)とします。 極端な場合、k = m。
- EMバージョン:

- GDバージョン:
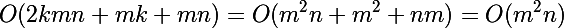
一般的に、数学的には、両方のアルゴリズムは同じレベルにありますが、どちらかがやや高いことがわかっています。
ここですべてのコードを見つけることができます 。