少し前まで、あるソーシャルネットワークの広大さのどこかで、次のゲームを見ました：プレイヤーは正の整数でホストに送信します（それを呼び出しましょう）（プレイヤーはお互いの番号を知らない）、最小の一意の番号を送信した人が勝ちます。 たとえば、7人のプレイヤーがプレイし、5、4、2、1、1、2、6の数字を送信した場合、4の数字を送信したプレイヤーが勝ちます。 このゲームを「正しく」「プレイ」する方法は非常に興味深いものになりましたが、 n人のプレーヤーに独自のソリューションがある場合はかなり複雑でわかりにくいため、3人と4人のプレーヤーの特定のケースを検討します。
3人のプレーヤーの場合
{1、2、3}から選択
行きましょう。 まず、制限を導入します：プレイヤーは{1、2、3}からのみ数字を選択できるようにします（その後、自然数を選択する方が簡単で明白になります）。 私たちが今やろうとしていること：そのような混合戦略を見つける
すべてのプレイヤーがこの戦略を順守している場合、戦略を変更することで勝つ可能性を高めることはできません（そのようなことは、 ナッシュ均衡と呼ばれます）。 つまり、確率で各プレイヤーに 
確率1の数字を選択しました 
-番号2および確率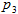 
-3 、および各プレイヤーがこれらの確率から逸脱することは利益がありません。
プレイヤー2と3がこれらの確率を使用し、プレイヤー1が勝つチャンスを増やすことに決め、今度は戦略を使用すると仮定します。
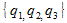。 勝つために、彼は番号1 （および残りのプレイヤーは両方2 、または両方3 、または1 2および2番目-3 ）を選択する必要があります、番号2 （残りは両方1または両方3を選択する必要があります）、または3 （この場合、他は両方とも1を選択するか、両方とも2を選択する必要があります）。 したがって、勝利の最終確率 
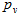これら3つの確率の合計として表すことができます。 
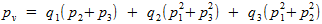（1）。 また、すべての確率の合計が最終的に単一であることを忘れないでください。 
（*）。
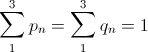そのため、プレーヤー1は勝つチャンスを増やす必要があります
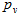ただし、制限があります（*）。 ラグランジュ乗数の素晴らしい方法は 、私たちが必要なことだけを行うレスキューに来ます-それは、いくつかの平等（既存の平等（*））の既存の制限の下で、関数の局所的な極値（関数（1）があります）を見つけます。 ラグランジュ方程式 
次の方程式が得られます。
、
もちろん、平等（*）を考慮して解決します。 次の確率が得られます。
できた！ 結論はどれですか？ 3人のプレイヤーが{1、2、3}からのみ選択できる場合、それぞれの最適な戦略は次のとおりです。ケースの約半分で1を選択し、約4分の1で2を選択し、約4分の1で3を選択します。 これがナッシュ均衡になります。
任意の自然数の選択
それでは、プレイヤーが数字を選択できるセットの制限を削除するとどうなりますか？また、そのようなゲームのナッシュ均衡をどのように見つけるのでしょうか？ プレイヤーが特定の番号iを選択した場合、すべてのプレイヤーが厳密にiよりも小さい同じ番号を選択するか、両方が厳密にiよりも大きい番号を選択した場合にのみ勝ちます。 したがって、各プレイヤーについて、勝利の確率
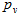以下： 
。 この方程式を微分すると、無限の数の方程式が得られます。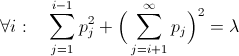 
および制限 
。 そのようなことは解決可能ですが、十分に難しいので、ここに答えを出してください：
。
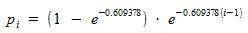これはどういう意味ですか？ 得られた方程式に特定の数値を代入すると、最初の7つの場合、およそ次の確率が得られます。
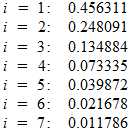
つまり、ナッシュ均衡は、各プレーヤーが約0.46の確率、0.25-2の確率、0.13-3の確率などで1を選択するような戦略のセットになります。
4人のプレーヤーの場合
4人のプレイヤーと同じゲームは、3人のゲームとそれほど違いはありません。 この場合、最大化される関数の形式は次のとおりです。
何ですか？
解決策は次のとおりです。
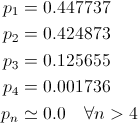
そのため、ほとんどの場合、数字の1と2を選択する必要があり、時には3 、非常にまれに4を選択する必要があり、4を超える数字を扱う必要はほとんどありません。
ご清聴ありがとうございました。 ゲームをする。