私が自分で設定した主なタスクは、理論的な知識を組み合わせて実用的な問題を解決することでした。 そのようなタスクは、レゴロボットドライブを制御することでした。 おもちゃを演奏するもう1つの理由と、生徒が厳しいマタンを認識しやすくする...このセットの説明の例を次に示します: habrahabr.ru/post/166449 。
順番に行きましょう。最初は、エンジンの適切な数学モデルを作成する必要がありました。 そしてすでにここで私は問題に遭遇しました:メーカーはキットのエンジンの技術的特性を示していませんでした。 Googleでの検索には多くのオプションがあります(例: nxt-unroller.blogspot.ru/2011/01/motor-controller-with-feed-forward-for.htmlまたはphilohome.com/nxtmotor/nxtmotor.htm )ロボットで使用されたエンジンの特性を取得することでした。 これは、物理学と理論力学の知識が役に立ちました。
ラグランジュ・オイラー方程式を作成し、DCモーター(DCT)のローターの巻線における逆起電力の影響を考慮に入れて、以下を取得します。
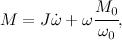
ここで、wはモーターの回転角速度、w0はアイドル速度、Mはエンジンが発生するモーメント、M0は開始モーメント、Jはエンジンローターの慣性モーメントです。 微分方程式の解は次の式です:
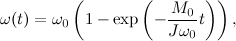
ここで、J * w0 / M0 = Tm、Tmはエンジンの電気機械定数です。
時間の角度を変更する関数は、初期条件を考慮した速度関数の積分になります。
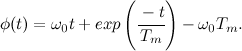
必要なだけです。
次に、示された式で記述されるDPTの加速の特性を取り除くプログラムを作成する必要がありました。 このために、Linux用のnxcEditorとWindows用のBricxccを使用しました。 出力で、角度の値と対応する時間の指示を含むファイルを受け取りました。
Scilab(Matlabのオープンアナログ)のエンジンからのデータを処理し、aa(2)= Tm = 0.081 [sec]およびaa(1)= w0 = 14.7 [rad]に等しい最小二乗法を使用して電気機械定数と定常エンジン速度の値を取得しました/秒]。
data=read("/home/kasper/Number.txt",-1,2); time=(data(:,2)-data(1,2))/1000; angle=data(:,1)*%pi/180; angle=angle'; time=time'; f=[time;angle]; function e=G(a, z), e = z(2) - a(1)*(z(1)-a(2)+a(2)*%e^(-z(1)/a(2))); endfunction a0=[1;4]; [aa,er]=datafit(G,f,a0); model=aa(1)*(time+aa(2)*(%e^(-time/aa(2))-1)); xtitle(' ','time','$\dot\phi,[\frac{}{}]$'); plot2d(time,model,[5]); a=gca(); a.children.children(1).thickness=2; plot2d(time,angle,[2]); a.children.children(1).thickness=2; a.children.children(1).text=["$\dot\phi(t)$"];
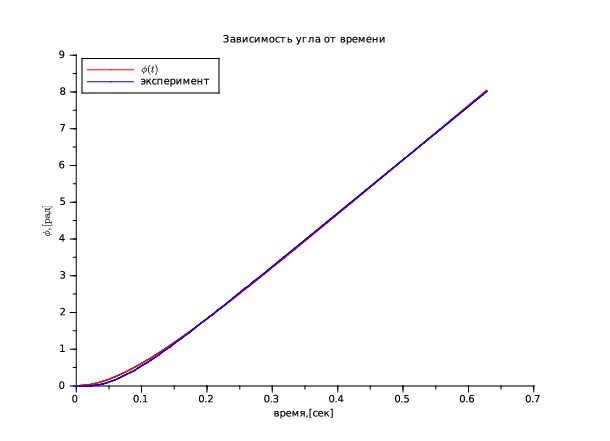
そして、正弦波の形で制御をエンジンに適用することにより、得られた値の妥当性を確認します(数学モデルと実際のエンジンの反応のグラフが画像に示されています、実際のエンジンのグラフは、時計回りと反時計回りに回転すると、モーター回路の抵抗の違いにより浮き上がります)電源キー):

これで、エンジンの構造定数の計算に安全に進むことができます。これは、モーメントを制御するために必要です。 これを行うために、電気プロセスを記述するエンジン方程式のシステムを使用しました。
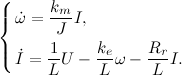
ここで、ke、kmは設計定数、U = 7 [V]は制御電圧、L = 0.0047 [H]は巻線インダクタンス、Rr = 6 [オーム]はロボット巻線の抵抗です。 彼は、開始電流I = 0.9 [A](ローターがロックされているときに測定)を測定し、ローターの慣性モーメントを計算しました。 次の式を使用して、エンジンが発する始動トルクを取得しました。

方程式のi = 48は削減係数です。 電流伝達係数は0.42で、出力軸の始動トルクを始動電流で除算しました
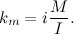
0.48に等しい透過の逆起電力係数は、印加角電圧に対する定常角速度の比として計算されました。
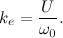
次のステップは、DPTの回転角度の制御をプログラムすることです。 このために、私は比例レギュレータを使用しました。 ソフトウェアの実装は次のとおりです。
#define NEED_ANGLE 180 #define WORK_TIME 3000 #define KOL_EXPS 3 #define PORT OUT_A #define KP 14 task main() { int angle_now, battery_voltage, power_percent, time = 0; int i, str_size, file_size = 8224; byte file; string str = "3lab.txt"; float need_voltage, angle_diff; DeleteFile(str); CreateFile(str, file_size, file); while(time < WORK_TIME) { angle_now = MotorRotationCount(PORT); time = CurrentTick() - FirstTick(); angle_diff = NEED_ANGLE - angle_now; angle_diff = angle_diff * 3.1415 / 180; need_voltage = KP * angle_diff; need_voltage *= 1000; battery_voltage = BatteryLevel(); power_percent = need_voltage / battery_voltage * 100; if(abs(power_percent) > 100) power_percent = 100 * sign(power_percent); OnFwd(PORT, power_percent); str = NumToStr(angle_now) + " " + NumToStr(time); WriteLnString(file, str, str_size); Wait(MS_5); } Off(PORT); CloseFile(file); }
そして、ここで真実の瞬間、計算されたモデルが実際の状況にどれだけ対応しているかがわかります(モデルはScilab Xcosで組み立てられました)。
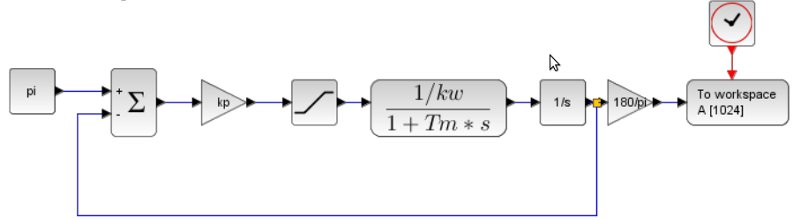
モデルと実験曲線を用意します。
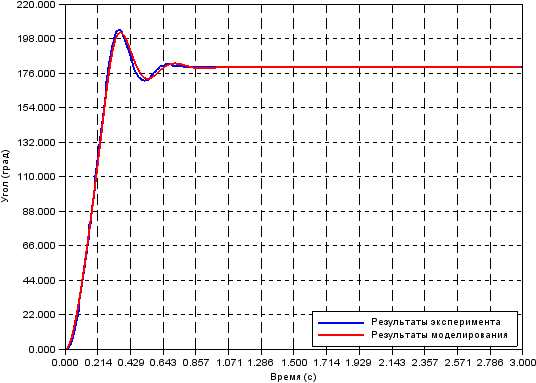
ご覧のとおり、すべてが3%以下の偏差で一致しています。
このような簡単な日曜大工実験により、数学的モデリングと制御理論の基礎を理解することができます。
次に、作業のパフォーマンスに関するマニュアルを共有する準備ができました。
ご意見やご提案をお待ちしております。