←最初の部分を読む
組み合わせとしての構成
量子力学の重要なポイントの1つは、構成が常に複数の粒子の状態を記述することです。 見てください:今回は、最初の記事の実験を少し複雑にしますが、 2つの光子をDに送信します-ポイントBとC
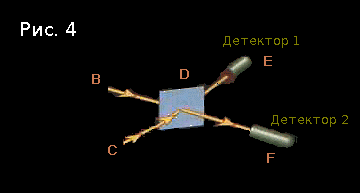
初期構成は「光子はBからDに飛ぶ、光子はCからDに飛ぶ」です。 前回と同様に、その振幅は(-1 + 0 i )であると仮定します。
Dには、すでにおなじみのハーフシルバーミラーがあります。これは、光子が反射されるときに振幅を1倍し、光子が通過するときに-iを乗算します(元々はiでしたが、これは完全に真実ではありません- およそTrans。 )。
次の4つのケースを検討してください。
- 両方の光子が反射されました。 (−1 + 0 i )× -i × -i =(1 + 0 i )に等しい振幅は、「光子はDからEに、光子はDからFに飛ぶ」という構成を考慮しています。
- Bから飛ぶ光子が反射しました。 Cから飛んでくる光子が通り過ぎた。 (-1 + 0 i )× -i ×1 =(0 + i )に等しい振幅は、「2つの光子がDからEに飛ぶ」という構成を考慮に入れています。
- Bから飛んでいる光子が飛んできました。 Cから飛ぶ光子が反射されます。 (-1 + 0 i )×1× -i =(0 + i )に等しい振幅は、「2つの光子がDからFに飛ぶ」という構成を考慮に入れています。
- 両方の光子が飛んだ。 (−1 + 0 i )×1×1 =(−1 + 0 i )に等しい振幅は、「光子はDからEに、光子はDからFに飛ぶ」という構成を考慮しています。
最初のケースと4番目のケースでまったく異なる状況が同じ結果の構成につながったことに注意してください! したがって、「フォトンがEに、フォトンがFに飛ぶ」構成の最終値を考慮すると、(1 + 0 i )+(−1 + 0 i )= 0になります。これは、これが起こらないことを意味します。 。 両方の検出器を同時に使用することはできません。
この実験から学ぶべき重要な教訓: 光子は見分けがつかない 。 2つの光子にわずかな違いさえあれば、実験の結果は完全に異なります。
振幅を確率と見なすことができる世界の古典的なモデルでは、結果をグループ化する方法を誰でも自由に選択できます。 説明してみましょう。上記の4つの結果はすべて異なると考えることができます。 2つの結果のみを区別できます(「各光子が光子に到達する」と「両方の光子が単一の検出器に到達する」)。 他の何かをすることができます。 そして、何も変わらなかっただろう。 同様に、奇数が2つのサイコロで落ちる確率を計算する必要がある場合、スローの36の可能な結果のプレートを作成できますが、エッジをすぐに「偶数」と「奇数」に分割し、結果の数を4つに減らすことができます。
なぜこれが量子モデルで機能しないのですか? イベントの確率は非線形に振幅に依存するため、ご存知のように、平方和は平方和で置き換えることができません。
((2 + i )+(1 + -i )) 2 =(3 + 0 i ) 2 = 3 2 + 0 2 = 9
(2 + i ) 2 +(1 + -i ) 2 =(2 2 + 1 2 )+(1 2 +(−1) 2 )=(4 + 1)+(1 + 1)= 7
このことから、どの構成が異なっており、どの構成が異なっていないかを実験的に確認できることがわかります。 特に、これらの構成は同一です。
- 「 Bからの光子はDに反射され、 Eに飛びます。 光子Cは Dに反射され、 F "に飛びます。
- 「 Bからの光子がDを経由してEに飛ぶ。 光子CはDを通過してFに到達します。
そして、ここに2番目の重要なレッスンがあります(最初の段落で示唆し、後で詳しく説明します)。 量子力学の法則は個々の粒子には適用できません 。 ここでは、分割統治戦略は機能しません。 これは大きな誘惑です-各素粒子の振る舞いを考慮し、モザイクの一部から世界の全体像を何らかの形で追加することは特に困難ではありません...しかし、このアプローチが量子力学の開発を長年にわたって妨げてきました。
さまざまな構成
すぐに角の近くで雄牛を捕まえます。 2つの構成が異なるのはいつですか?
この質問に答えるために、次の実験を実施します。

ポイントSはセンサーです。 彼が行う唯一のことは、光子が通過するときに別の状態になることです。 実験の開始時には、センサーは
状態にあり、通過する光子がセンサーを
状態にすると仮定します。
したがって、初期構成:
- 「光子はAに向かって飛ぶ。 状態
S =(-1 + 0 i )
光子がAに到着した後はどうなりますか? センサーなしのこの実験の前のバージョンでは、可能な構成は、振幅iの 「フォトンフライAからB 」および振幅-1の「フォトンフライAからC 」でした。 ただし、各構成はシステムの完全な状態を記述するため、説明にセンサーの状態を含める必要があります。 だから:
- 「光子はAからBに飛ぶ。 状態「
」のS =(0 + i ) - 「光子はAからCに飛ぶ。 状態
S =(-1 + 0 i )
ミラーBとCが登場します。
- 「光子はBからDに飛ぶ。 状態
S =(-1 + 0 i ) - 「光子はCからDに飛ぶ。 状態
S =(0 + i )
最後に、セミミラーD :
- 「光子はDからEに飛ぶ。 状態「
」のS =(0 + i ) - 「光子はDからFに飛ぶ。 状態
S =(-1 + 0 i ) - 「光子はDからEに飛ぶ。 状態
S =(0 + i ) - 「光子はDからFに飛ぶ。 状態
S =(1 + 0 i )
覚えておいてください: センサーなしでこの実験を行ったとき、結果#1と#3は互いに「中和」されました。それらに対応する構成は同一だったからです。 しかし、現在は同じではありません。すべてSセンサーのおかげです。 4つの構成すべての振幅モジュールの2乗は等しく、この実験を実際に行った場合、両方の検出器が同じ周波数で動作することを確認します。 ( もちろん、私が何も台無しにしないなら、私は個人的に実験を行いませんでした。)
センサーの状態を気にしない場合も同じことが起こります。 物理学の法則は、私たちの考えと同じように無関心です。
光子がSを通過したかどうかを確認することさえしなければ、同じことが起こります。 構成#1と#3は異なります-他に何も必要ありません。
Sの存在をまったく知らない場合も同じことが起こります 。
実験が宇宙で行われ、 Sが
状態の場合は1方向に、
状態の場合はもう1方向に単一光子を送信することで状態を通知します。 私たちにとって、そうではないことはまったく同じです。 しかし、宇宙全体の1つの粒子は別の場所にあり、これで十分です。
(しかし、 Sが構成空間で十分に大きい場合、同じことは起こりません。この場合、 Sに対する光子の影響は別の結果を形成するのに十分ではないかもしれません。構成空間は実際に連続である、離散的ではありません。)
ここで、このような実験をしている人が振幅と構成について何も知らない場合に考えていることを想像してみましょう。
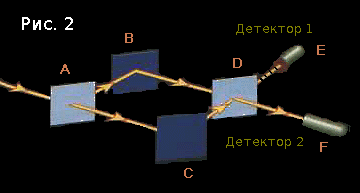
実験者は、a)光子が最初の検出器に到達することを望まず、b)経路の1つがブロックされると、光子が突然両方の検出器に到達し始めますが、それらが分離されることはありません。 うん
第一に、彼は粒子を扱っていると考えています-観察しているのは個々の光子であり、それぞれの光子は(信じているように)各瞬間に厳密に定義された位置にあります。 これは論理的ですが、偽です。
第二に、彼は特定の... 神秘的な現象の存在を確信しています...それは光子が最初の検出器に現れることを許しません。 このためには、光子がいずれかの検出器に入る機会が必要です。 たとえ最終的に彼は常に2番目を選択します。
cな光子は邪魔されたくないだけでなく、道に沿って歩いていなくても 、道が塞がれていることを知っています。 ここで何が起こっているのですか?
実験者は、光子が毎回選択する経路を追跡するために、 AとCの間にセンサーを配置することにしました。

そして、神秘的な現象は風によって吹き飛ばされました。
これから、長い間妄想的になります。
21世紀では、光子に何が起こったのかを「知る」ことは、脳内の粒子の隔壁の位置を変えることに等しいことをすでに認識していました。 センサーから未知の方向に放出された1個の光子でも構成を変えて振幅の減少を防ぐのに十分であれば、光子を捕らえる高度な測定デバイスで十分です。
しかし、もしあなたがこれらすべてを考えていなければ、あなたの情勢は悪いです。 あなたの考えは、わずかに異なる方向に進む可能性があります。
光子は、両方の方向に進むための物理的な能力を持つだけではありません-センサーはそれに対して完全に透過的です。 すべてがはるかに悪いです。 光子は、あなたが彼がどこにいて何をしているのかをあなたに知ってほしくありません。
ここで光子が飛んだことを確実に知っていれば、他のすべての可能性は幾分信じられないものになるでしょう。 これは、その経路内の実際の障害物以上に光子を妨害します。 重要なことは、何が起こったのかではなく、何が起こる可能性があるかです。 あなたが知っていること-むしろ、理論的に知ることができること-が決定要因です。
部屋で緊急! 意識的な理解は実験結果に影響を与えます! 理由はまだ第一です!
ええ 実験の過程を「観察する」単純な石が同じ効果をもたらすことに気づくのは本当に大変でしたか? おそらく石にも意識がありますか?
しかし、後知恵では、誰もが賢いです。 当時住んでいたら、ジョン・フォン・ノイマンよりもうまくやっていただろうと思いませんか? そのときの主なことは、妄想ではあるが理論が正しい予測を与えることでした。 壊れていないものは修理しないでください。すべてがうまくいきます。
←最初の部分を読む