MIDIシンセサイザー、ギターの和音を認識するアルゴリズムを使用してプログラムでサウンドを再生する方法に興味がある場合、またはギターやキーボードを演奏するだけの場合は、カットをお願いします。
1、1、2、3 ...
キーボードを書く前に、何らかの方法でサウンドを演奏する方法を学ぶ必要があります。 最初に思い浮かぶのは、システムに組み込まれたシンセサイザーを使用することです。 それはすべてのデバイスにあり、何もインストールする必要はありません。 一般に、そのまま使用できます。
私はC#でプログラムを書くことにしました。 Googleで検索したところ、.NET自体はMIDIの操作方法を知らないことがわかりましたが、これにはWinAPI関数があります。 その後の検索で、最終的にNAudioライブラリに移動しました。 それを使用して、サウンドを再生します。
メモを再生するには、特定のメッセージをMidiOutに送信して、再生チャンネル、メモ、および押圧力を示します。
したがって、たとえば、3オクターブのノートを演奏できます。
midiOut.Send( MidiMessage.StartNote( 57, 127, 0 ).RawData ) //id , (0-127), ;
しかし、すべてがそれほど単純なわけではないため、音符の再生を停止する必要があります。
midiOut.Send( MidiMessage.StopNote( 57, 0, 0 ).RawData );
再生する前に、目的のMIDIデバイスを開く必要があります。 これは、単にMidiOutオブジェクトを作成することによって行われます。 デバイス番号はコンストラクタに渡されます、なぜなら いくつかあるかもしれません。
静的プロパティMidiOut.NumberOfDevicesを読み取って番号を確認し、MidiOut.DeviceInfoメソッドを使用してこのデバイスに関する情報を取得し、シンセサイザーIDを渡します。
その奇妙な数57を覚えていますか? これはノート識別子です。 番号付けは0から始まり、後続の各値は半音ずつ調性が増加します。
演奏されたノートのIDへの依存は、テーブルで見ることができます:
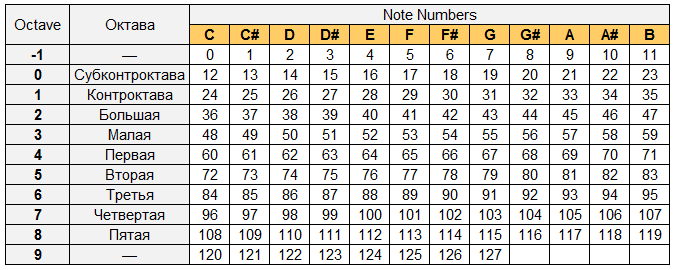
これらすべての情報を読んだ後、NAudioの操作を簡素化するクラスを作成しました。
非表示のテキスト
internal struct Note { public Note( byte oct, Tones t ) { octave = oct; tone = t; id = 12 + octave * 12 + (int)tone; } public byte octave; public Tones tone; public int id; } public enum Tones { A = 9, Ad = 10, B = 11, C = 0, Cd = 1, D = 2, Dd = 3, E = 4, F = 5, Fd = 6, G = 7, Gd = 8 } class AudioSintezator : IDisposable { public int PlayTone( byte octave, Tones tone ) { // 12 , 0- ( -1-) int note = 12 + octave * 12 + (int)tone; if( !playingTones.Contains( note ) ) { // . 0 midiOut.Send( MidiMessage.StartNote( note, 127, 0 ).RawData ); playingTones.Add( note ); } return note; } public void StopPlaying( int id ) { if( playingTones.Contains( id ) ) { // midiOut.Send( MidiMessage.StopNote( id, 0, 0 ).RawData ); playingTones.Remove( id ); } } MidiOut midiOut = new MidiOut( 0 ); List<int> playingTones = new List<int>(); public void Dispose() { midiOut.Close(); midiOut.Dispose(); } }
また、MIDIキーボードの試用版を作成しました
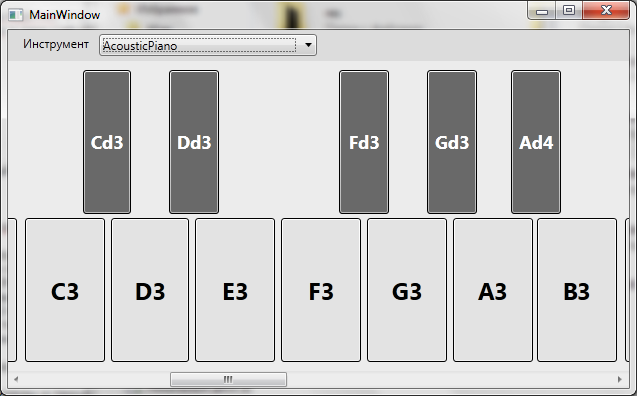
セックス、ドラッグ、ロックンロール
次の段階は、ギターのネックの作成と、弦とフレットへのノートのバインドです。
ギターのフレットボードは非常にシンプルです。 開いた位置にある各弦は、特定の音色の音を出します。 特定のフレットにクランプされた同じ弦は、サウンドを特定の半音数だけ高くします(1フレット-1半音)。
開いた弦がE4の音を出す場合、2番目のフレットに固定され、F#4の音と12番目のE5で音を生成します。
アルゴリズムは単純です。開いている文字列をメモし、特定の半音数だけ増やします。
私の人生を簡素化するために、私はクラスを書きました:
非表示のテキスト
class Guitar { public Guitar( params Note[] tune ) { for( int i = 0; i < 6; ++i ) { strs.Add( new GuitarString( tune[i] ) ); } } public List<Tuple<byte, byte>> GetFretsForNote( Note note ) { // 1- ( 0 5), 2- - ( 0 - ) List<Tuple<byte, byte>> result = new List<Tuple<byte, byte>>(); byte currentString = 0; foreach( var str in strs ) { var fret = str.GetFretForNote( note ); if( fret != -1 ) // { result.Add( new Tuple<byte, byte>( currentString, (byte)fret ) ); } ++currentString; } return result; } public Note GetNote( byte str, byte fret ) { return strs[str].GetNoteForFret( fret ); } public void SetTuning( params Note[] tune ) // { for( int i = 0; i < 6; ++i ) { strs[i].SetTune( tune[i] ); } } List<GuitarString> strs = new List<GuitarString>(); } class GuitarString { public GuitarString( Note note ) { this.open = note; } public void SetTune( Note note ) { this.open = note; } public Note GetNoteForFret( byte fret ) { return open + fret; } public int GetFretForNote( Note note ) { int fret = -1; // -1 , if( open <= note ) { int octDiff = note.octave - open.octave; int noteDiff = note.tone - open.tone; fret = octDiff * 12 + noteDiff; } return fret; } Note open; }
この段階で得たものは次のとおりです。
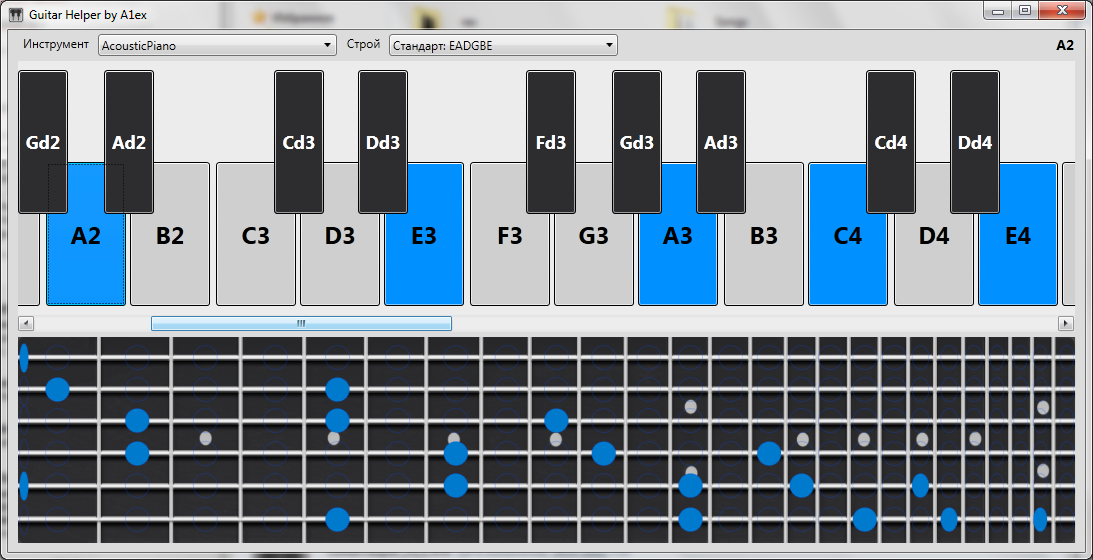
トライアド、セブンスコード、その他の音楽の喜び
この段階も、1つの点を除いて特に複雑ではありません。1つの点については、後ほど説明します。
ちょっとした理論:コードは特定のキーの音のセットです。 これらのメモはとにかく取られません-それらは特定の間隔で配置されます。 間隔は半音単位で測定されます。
たとえば、Aマイナーのコードの間隔は3.4です。 音符のシーケンスを表します:A、C、E(la、do、mi)
これについてはもう話せません。 音楽のアマチュア、音楽院は終わりませんでした。 そして、私は多くの不必要で真実とは程遠いことを言うのを恐れています。 詳細はウィキペディアで見つけることができます。
プログラムに戻ります。
認識アルゴリズムは次のとおりです。
- 最も低い音を見つけます。それが和音の基礎になります(私が間違っていなければ、音が大きい)
- 「隣接する」音符の間隔を考慮します
- 事前準備された間隔テーブルを確認します
これは、1つではないにしても、完了できた可能性があります。ギターのコードは、アレンジされるほど単純ではありません。 特定の範囲の多くの音が含まれています。 たとえば、Aマイナーのギターにはすでに5つのサウンドが含まれていますが、同じla-do-miです。
これにより、認識が複雑になります。
- ノートのリストを作成し、そこから繰り返し音を削除します(たとえば、最大で異なるオクターブ)
- それらを近づけて、1オクターブまたは数個の距離を削除します
- 間隔の表に従ってチェックします。 一致するものが見つからない場合は、次に進みます。
- 考えられるすべての組み合わせ(順列)を並べ替えて、表を確認します。
- それでも見つからない場合は、コードを不明と呼びます。
おそらく既にご想像のとおり、コードの操作を簡素化するクラスも作成しました。
非表示のテキスト
static class Chords { public static ChordType[] chordTypes = new ChordType[]{ new ChordType(" ", "", 4,3), new ChordType(" ", "m", 3,4), new ChordType(" ", "5+", 4,4), new ChordType(" ", "m-5", 3,3), new ChordType(" ", "maj7", 4,3,4), new ChordType(" ", "m+7", 3,4,4), new ChordType("", "7", 4,3,3), new ChordType(" ", "m7", 3,4,3), new ChordType(" ", "maj5+", 4,4,3), new ChordType(" ", "m7-5", 3,3,4), new ChordType(" ", "dim", 3,3,3), new ChordType(" (IV)", "sus2", 2,5), new ChordType(" (II)", "sus4", 5,2), new ChordType("","6", 4,3,2), new ChordType("", "m6", 3,4,2), new ChordType(" ", "9", 4,3,3,4), new ChordType(" ", "m9", 3,4,3,4), new ChordType(" ", "-9", 4,3,3,3), new ChordType(" ", "m-9", 3,4,3,3), new ChordType("",""), new ChordType(" ", " - 2", 1), new ChordType(" ", " - 2", 2), new ChordType(" ", " - 3", 3), new ChordType(" ", " - 3", 4), new ChordType(" ", " - 4", 5), new ChordType(" ", " - 4", 6), new ChordType(" ", " - 5", 7), new ChordType(" ", " - 6", 8), new ChordType(" ", " - 6", 9), new ChordType(" ", " - 7", 10), new ChordType(" ", " - 7", 11), new ChordType("", " - ", 12), new ChordType(" ", " - 9", 13), new ChordType(" ", " - 9", 14) }; public static string[] chordsBases = new string[] { "A","A#","B","C","C#","D","D#","E", "F","F#","G","G#" }; public static string[] chordMods = new string[] { "","m","5+","m-5","maj7","m+7","7", "m7","maj5+","m7-5","dim","sus2","sus4", "6","m6","9","m9","-9","m-9" }; private static int GetChordType( List<Note> tmp ) { int[] intervals = new int[tmp.Count - 1]; for( int i = 0; i < tmp.Count - 1; ++i ) { intervals[i] = tmp[i] - tmp[i + 1]; } int type = 0; foreach( var chordType in Chords.chordTypes ) { if( Utils.CompareArrays( intervals, chordType.intervals ) ) break; ++type; } return type; } public static void GetChord( List<Note> chordNotes, out Note BaseNote, out ChordType type ) { List<Note> notes = PrepareNotes( chordNotes ); // int typeIndex = GetChordType( notes ); // if( typeIndex < chordTypes.Length ) // { BaseNote = notes[0]; type = chordTypes[typeIndex]; } else { bool unknown = true; var possibleChord = new List<Note>( notes ); // foreach( List<Note> perm in Utils.GeneratePermutation( possibleChord ) ) { // ( > 12 ) for( int k = 1; k < perm.Count; ++k ) { if( perm[k].tone > perm[k - 1].tone ) { perm[k] = new Note( perm[k - 1].octave, perm[k].tone ); } else { perm[k] = new Note( (byte)(perm[k - 1].octave + 1), perm[k].tone ); } } typeIndex = GetChordType( possibleChord ); if( typeIndex < Chords.chordTypes.Length ) { unknown = false; break; // , } } if( unknown ) { throw new Exception( " " ); } else { BaseNote = possibleChord[0]; type = chordTypes[typeIndex]; } } } private static List<Note> PrepareNotes( List<Note> notes ) { List<Note> tmp = new List<Note>(); bool finded = false; for( int i = 0; i < notes.Count; ++i ) { finded = false; var note = notes[i]; for( int j = 0; j < tmp.Count; ++j ) // { if( note.tone == tmp[j].tone ) { finded = true; break; } } if( !finded ) // { tmp.Add( note ); } } // , if( tmp.Count == 1 && notes.Count > 1 ) return notes; // "" byte lowest = tmp[0].octave; var lowesTone = tmp[0].tone; for( int i = 0; i < tmp.Count; ++i ) { if( tmp[i].octave > lowest ) { if( Utils.CountOfTones( tmp[i].tone, notes ) > 1 ) { if( tmp[i].tone > lowesTone ) { tmp[i] = new Note( lowest, tmp[i].tone ); } else { tmp[i] = new Note( (byte)(lowest + 1), tmp[i].tone ); } } } } tmp = tmp.OrderBy( x => x.id ).ToList(); return tmp; } }
最終結果:
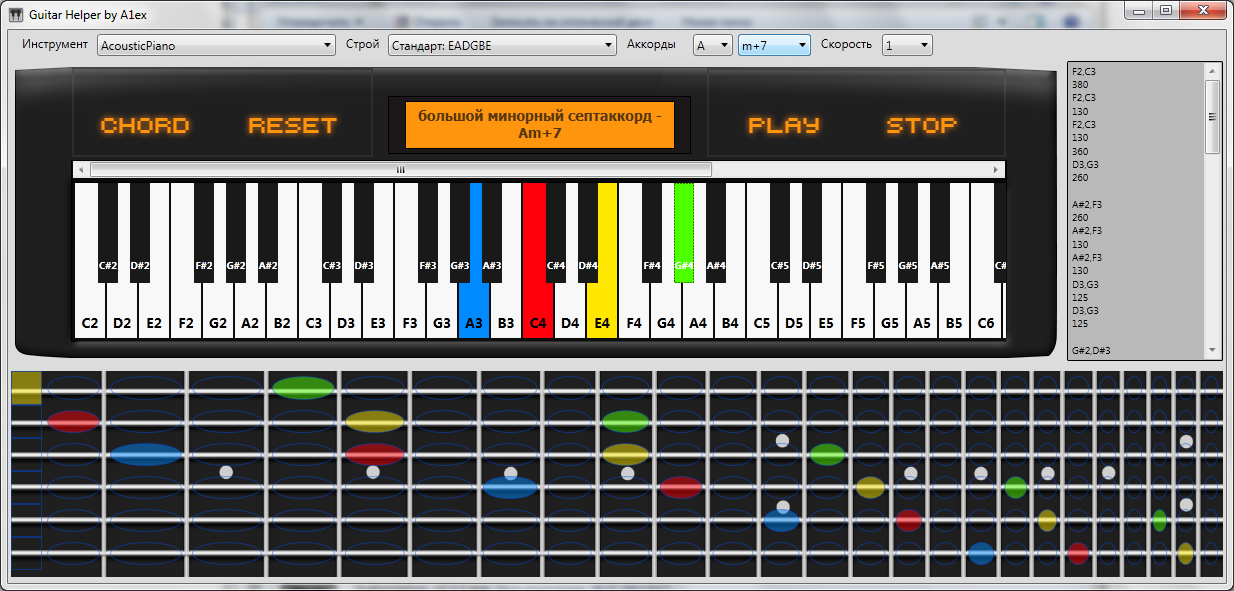
プロジェクトの完全なソースコードはGitHubで入手できます 。
また、投稿「Ovation。」の著者である同志サドラーにも感謝します。 JSとHTML5を使用した自分で作成できるコードチャート”から、コードチャートを作成しました。 少し時間を節約できました。