👩🏾‍🔬 🛀🏾 👶🏽 フィボナッチ数計算アルゴリズムの比較 🎞️ 📍 👲🏻

記事へのコメントでは、 OのN番目のフィボナッチ数（log N）とフィボナッチ数を計算する別のアルゴリズムは、すでに100番目のフィボナッチ数が4バイトに収まらないという事実を示し、「長い」算術では乗算の速度が急です。たるみさらに、プリミティブの追加がより高速になる可能性があるという提案がありました。 2つのアルゴリズム-単純な加算と対数の数の演算を行うアルゴリズム-を比較することにし、Cでテストプログラムを作成しました。「長い」算術演算にはGMPライブラリを使用しました。

テストプログラムのテキスト

#include <stdio.h> #include <stdlib.h> #include <time.h> #include <gmp.h> void fibonachi1(unsigned int n, mpz_t result); void fibonachi2(unsigned int n, mpz_t result); void dump(unsigned int n); int main(int argc, char* argv[]) { unsigned int n, test_count; clock_t t1, t2; mpz_t result; scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi1(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi2(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } // dump(10000); return 0; } void fibonachi1(unsigned int n, mpz_t result) { mpz_t last, current; if (n < 2) { mpz_init_set_ui(result, n); } else { mpz_init_set_ui(last, 0); mpz_init_set_ui(current, 1); while (--n > 0) { mpz_swap(last, current); mpz_add(current, current, last); } mpz_swap(current, result); mpz_clear(last); mpz_clear(current); } } void fibonachi2(unsigned int n, mpz_t result) { mpz_t fn, fn1, gn, gn1; if (n < 2) { mpz_init_set_ui(result, n); } else { unsigned mask = 1, m = n; while (m > 1) { m >>= 1; mask <<= 1; } mpz_init_set_ui(fn, 1); mpz_init_set_ui(fn1, 1); mpz_init(gn); mpz_init(gn1); while (mask > 3) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_set(fn1, fn); mpz_addmul(fn, gn, gn); mpz_mul(gn, gn, gn1); mpz_add(fn1, fn1, gn); mpz_add(fn1, fn1, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_mul(gn, gn, gn); mpz_sub(fn, fn, gn); mpz_mul(fn1, gn1, gn1); mpz_add(fn1, fn1, gn); } } if (mask > 1) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_addmul(fn, gn, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_submul(fn, gn, gn); } } mpz_swap(result, fn); mpz_clear(fn1); mpz_clear(gn); mpz_clear(gn1); } } void dump(unsigned int n) { FILE* output; mpz_t result; mpz_init(result); fibonachi1(n, result); output = fopen("alg1.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); mpz_init(result); fibonachi2(n, result); output = fopen("alg2.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); }

テストを実行するプリミティブスクリプト

 #!/bin/bash ./main <input.txt >test1.txt ./main <input.txt >test2.txt ./main <input.txt >test3.txt

入力データ：

 15 200000 400000 600000 800000 1000000 1200000 1400000 1600000 1800000 2000000 2200000 2400000 2600000 2800000 3000000 13 50000000 100000000 200000000 300000000 400000000 500000000 600000000 700000000 800000000 900000000 1000000000 1100000000 1200000000

テスト環境：VirtualBox、Athlon II X3 3.4 GHz、1 GB RAM、Xubuntu 12.04 64ビット、GCC 4.6.3コンパイラ、O2最適化

2番目のアルゴリズムははるかに高速であることが判明しました。 10番目のフィボナッチ数を計算する最初のアルゴリズムを待つことができませんでした。アルゴリズム2は、これを行うのに21秒かかりました。

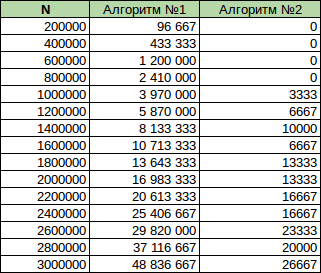
結果（clock（）関数が返す時間で示されます）：

2番目のグラフはO（N）に非常に似ています。最初のアルゴリズムのグラフは、O（N ^ 2）により類似しています。

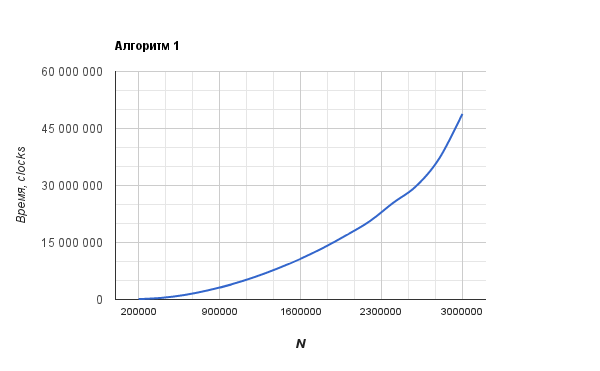
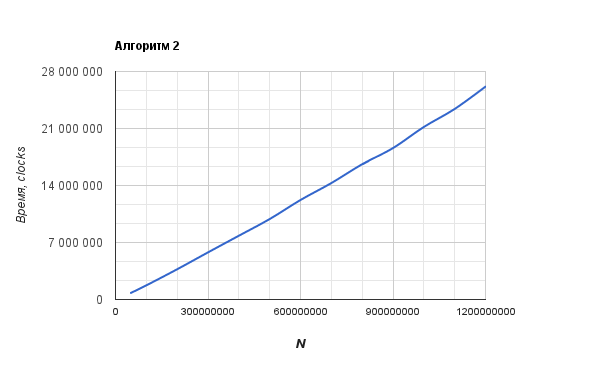
UPD複合スケジュールが追加されました。 2番目のアルゴリズムは非常に高速に動作するため、実行時間はclock（）関数のエラーに匹敵します。

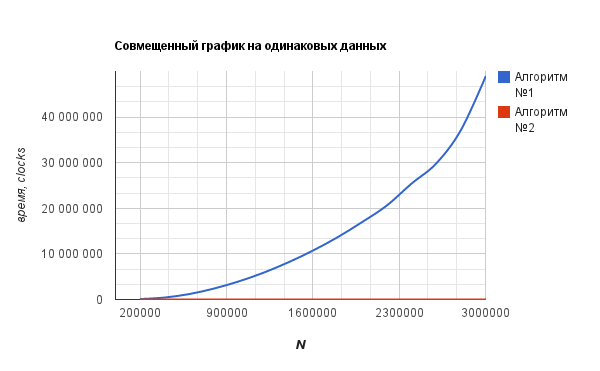
チャートが構築されるデータ：

フィボナッチ数計算アルゴリズムの比較

More articles: