Clever Geek Handbook

単一行のC / C ++。 パート2



以前、私はすでにC ++という単一行に関する記事を公開していました。 そのため、この投稿では、さらにいくつかのアルゴリズムと、2つの数値を交換するアルゴリズムのいくつかの実装（稼働時間の計算を含む）について言及したいと思います。

興味のある方はカットをお願いします;）





1.シンプルさをテストする



この関数を呼び出すには、 prime(100, int(sqrt(100))); 





 bool prime(int n, int div) { return ( div == 1) ? true : (n % div != 0) && (prime(n, div-1)); }


これを回避するには、ラッパー関数を作成できます。 

 bool prime(int n) { return ( n == 1 )? 0 : ( prime( n, int(sqrt(n))) ) ; }


そして今、関数を呼び出すには、 prime(100)



書くだけです



2.グレイコード



グレイコードは、2つの隣接する数字のコードが1ビットだけ異なる場合に、負でない数字に番号を付けるシステムです。 

 int codeGrey (int n) { return n ^ (n >> 1); }


グレイの逆コードを見つけるだけでなく 

 int revCodeGrey (int g) { int n; for (n=0; g; n ^=g, g>>=1); return n; }


グレーコードには、さまざまな分野でいくつかの用途があります。





3.二項係数の計算



二項係数は、ニュートンの二項の展開の係数です 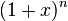画像 xの累乗。 

 int binomialCoefficient(int k, int n) { return (n==k || k==0)?1:binomialCoefficient(k-1,n-1)+binomialCoefficient(k,n-1); }




4.階乗除数の程度を見つける



[n]と[k]の2つの数字が与えられます。 除数[k]が数[n]に含まれる度合いを計算する必要があります。 

 int factPow(int n, int k) { return (n)? (n/k + factPow(n/k, k)):0; }




5.数[a]の累乗[b]モジュロ[p]。 



 nt powM(int a, int b, int p) { return b ? (a * powM(a-1, b, p) % p) : 1; }


ここでもインドのべき乗アルゴリズムを使用できます。 

 int powM(int a, int b, int p) { return b ? ((b&1?a:1)*powM(a*a, b/2, p) % p) : 1; }








SWAPaの私の研究



それで、私はさまざまなSWAPを探索するというアイデアを得ました。

SWAPテストはそのようなプログラムになります 
  int a=1, b=2; for(int i=0; i<=300000000; i++) { swap(&a, &b); }


スワップの代わりに、2つの値を交換するための異なるアルゴリズムがあります。



SWAP0


それでは、STLIvsky標準アルゴリズムから始めましょう。 

 template <class T> void swap0 ( T& a, T& b ) { T c(a); a=b; b=c; }


彼の指標は次のとおりでした。 

  1,996 sec. 1,986 sec. 1,996 sec.




SWAP1


次のSWAPは、いわゆるXOR SWAPです。 

 void swap1(int *a, int *b) { *a ^= ( *b ^= ( *a ^= *b )); }




彼の指標は次のとおりでした。 

  3,603 sec. 3,603 sec. 3,608 sec.




SWAP2 


 void swap2(int *a, int *b) { *a += *b -= *a = *b - *a; }


彼女の指標は次のとおりでした。 

  3.728 sec. 3.723 sec. 3.728 sec.




SWAP3 


 void swap3(int *a, int *b) { *a /= *b = (*a= *a * (*b)) / (*b); }


彼女の指標は次のとおりでした。 

  7.878 sec. 7.862 sec. 7.862 sec.




SWAP4 


 void swap4(int *a, int *b) { *b= *a + *b - (*a = *b); }


彼女の指標は次のとおりでした。 

  2.012 sec. 2.007 sec. 2.012 sec.




SWAP5 


 void swap5(int *a, int *b) { *a=(*b=(*a=*b^*a)^*b)^*a; }


彼女の指標は次のとおりでした。 

  3.198 sec. 3.213 sec. 3.198 sec.




SWAP6


さて、GCCコンパイラのアセンブラ挿入 

 void swap7(int *a, int *b) { asm volatile( "XOR %%EAX, %%EBX; \n\t" "XOR %%EBX, %%EAX; \n\t" "XOR %%EAX, %%EBX; \n\t" :"=a"(*a),"=b"(*b) :"a"(*a),"b"(*b) ); }


彼女の指標は次のとおりです。 

  2.199 sec. 2.153 sec. 2.167 sec.




ご覧のとおり、私たちの調査表は次のとおりです。 

  1.  SWAP0 - 1.992 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  2.  SWAP4 - 2.010 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  3.  SWAP6 - 2.173 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  4.  SWAP5 - 3.203 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  5.  SWAP1 - 3.604 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  6.  SWAP2 - 3.726 sec.
      
      
    
        
        
        
      
    
    
        
        
        
      
      
    
        
        
        
      
    
    
     
  7.  SWAP3 - 7.867 sec.


More articles:


All Articles