まず、累積分布関数は任意の値セットで定義できることを思い出しますが、それら自体は0〜1の値を持ちます。つまり、特定のセットの値を0〜1の厳密に定義された範囲に変換します。 。 たとえば、通常の関数は、マイナスの無限大からプラスの無限大までの範囲をこの悪名高い（0,1）に「アーカイブ」します。 対数正規分布は、0から無限の範囲のみを「アーカイブ」します。 などなど。
「解凍」のプロセスを想像してください。 これは、逆分布関数によって実行されます。 これらは分位関数とも呼ばれます。 ポイントはすでに理解しています。これらの関数は、範囲（0,1）をこの関数で指定された値の範囲に変換します。 もちろん、これらすべてには多くの制限がありますが、「視覚的なプレゼンテーション」の場合、このような比較は非常に適しています。
興味深いことに、1つの原則に従って（たとえば、標準正規分布に従って）生成された10 ^ 6のランダム変数と、対数正規分布の法則に従って別の10 ^ 6を取得した場合：
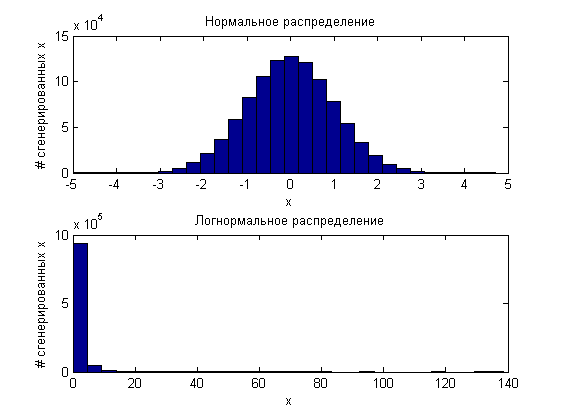
そして、それらを「アーカイブ」すると、受信した100万個の値の両方が0から1に均等に分配されます。
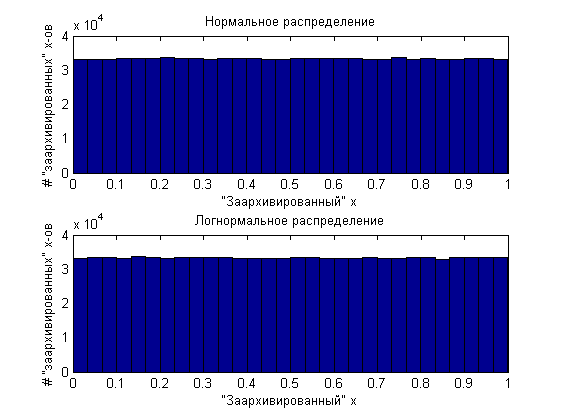
つまり、実際には、均一に分布した量と逆分布関数から任意の分布を生成できます。 そのような機能があるでしょう。 この教育プログラムは終了します。
次に、コピュラを紹介します。 式の定義は次のとおりです。
ここで、uは「アーカイブされた」値です（u = F（x）、Fは周辺分布関数です）。 それを書くこともできます
つまり、いくつかの「アーカイブされた」数量の共同分布関数です。 あなたは言うことができます-「ええと...私たちは、「アーカイブされた」量がすべての配布機能に対して等しく配布されることを示しただけです。 これは個々の数量に当てはまりますが、一度に複数の数量を処理します。 2つの量があるとします。1つは正規分布で、もう1つは対数正規です。 まず第一に、それらは互いに独立しています。 限界（値を個別に考慮する場合）分布は、上記で既に示しました。 次に、それらの共同分布がどのように見えるかを示します。
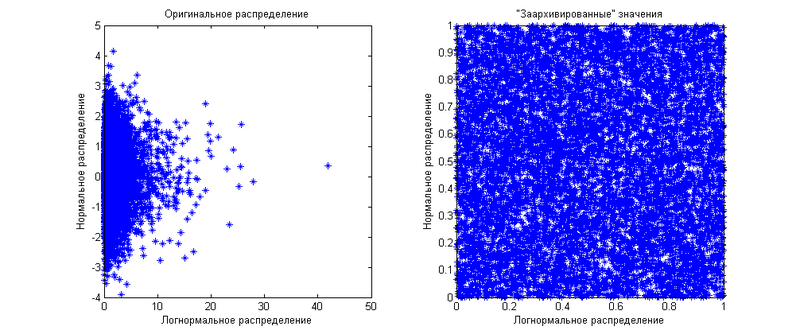
ご覧のように、「アーカイブされた」値は正方形に1 x 1で均等に分散されています。今度は同じ値を生成しますが、0.8に等しい相関があるとしましょう。 結果を次のグラフに示します。
ご覧のとおり、「アーカイブされた」値の分布は不均一になりました-対角線方向により集中しています。 ここでは、量の依存性の尺度としての相関の限定的な使用が明示されています。 それだけで操作すると、「アーカイブされた」値を対角線の近くまたはより遠くにのみ分散できます。 対角線は、相関が正の場合は45度、負の場合は135度になります。 しかし、異なる依存関係パターンを表示したい場合はどうでしょうか？ ここでコピュラがあなたの助けになります。 コピュラの式の定義から、2つの量がある場合、この正方形の分布関数が1 x 1で示されていることがわかります。 2つ以上ある場合、コピュラはn次元立方体の分布を1対1 ... 1で表示します。さまざまなコピュラを使用して、「アーカイブされた」数量の分布を表示できます。 コピュラのもう1つの重要な利点は、マージン分布からの独立性です。 つまり、周辺分布に値があるかどうかは気にしません。「アーカイブされた」値の依存関係によって表される依存関係を直接操作します。
コピュラはまだ確率関数であり、量の分布そのものではないため、各点が2つの量の結合確率に等しい表面としてグラフィカルに表示されます。 つまり、これは結合分布の密度のグラフです。 明確にするために、いくつかのコピュラの例を示します。
最初に、ガウスコピュラ自体の分布密度関数とそのグラフィカル表示を示します。
どこで
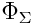正規分布関数であり、 
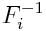i番目のマージン分布の逆関数、つまり特定の量自体の分布です。
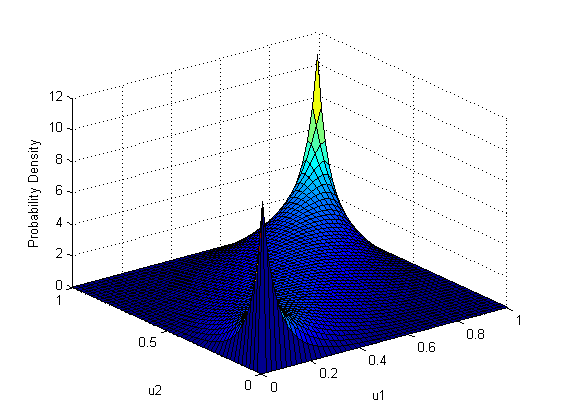
ご覧のとおり、これは最後の例の「アーカイブされた」ランダム変数の分布に非常に似ています。 これは奇妙なことではありません。前の例では、同じ相関パラメーターが0.8で、正規および対数正規の周辺分布関数を持つガウスコピュラを使用したためです。
次に、Studentコピュラを表示したいと思います。
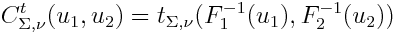
ここで、tは、指定された共分散行列と指定された数の自由度を持つ生徒分布関数です。
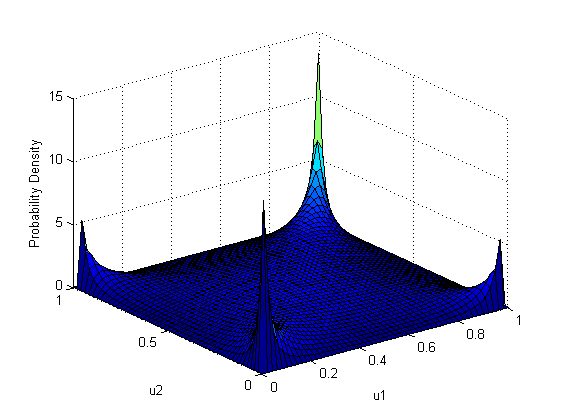
ガウス型コピュラとは異なり、スチューデントのコピュラは極値（1-1および0-0）でより大きな値を持っていることがわかります。これは、分布の裾が厚いことを意味します。 さらに高い値は角度0〜1および1〜0にあります。これは、限界関数の定義の範囲の端で顕著な逆関係を意味します。 このグラフは、値間の正の相関のために作成されたことに注意してください。 相関がゼロの場合、ガウス型コピュラとは対照的に、この場合は正方形全体に均一な分布があり、スチューデントのコピュラはすべての角度で同じ重みを持ちます。 これは、一方の値が「テール」値をとる場合、もう一方も「テール」値をとることになりますが、同じ確率で右または左になります。 コピュラの密度のグラフを読みやすくするために、精神的に軸の1つに垂直にスライスを作成できます。 結果のグラフは、別の値を修正するときに、ある「アーカイブされた」値が発生する確率密度のグラフになります。
また、厳密に1より大きくなければならないalphaパラメーターによってのみ2つの量の連結度を決定するClayton copulaを示したいと思います。
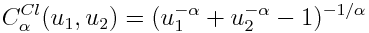
ここで、メインの重みは0〜0の角度にあります。つまり、値は辺縁関数の左端からの値を取る可能性が最も高くなります。
一般に、コピュラを使用すると、いくつかの量の依存関係を相互に示すことができるため、モデリングの範囲が広がります。 さらに参照するために、参照の小さなリストを提供します
Matlabのコピュラ
コピュラを使用した関係の理解 -エドワード・フリーズ、エミリアーノ・バルデス
コピュラへの対処 -Thorsten Schmidt