ノイズが存在する空間データをクラスタリングするための密度アルゴリズムのDBMSCAN(ノイズを伴うアプリケーションの密度ベースの空間クラスタリング)のMATLABでの実装を共有したいと思います。
特徴
DBSCANアルゴリズムは、1996年に、Martin Esther、Hans-Peter Kriegel、および同僚によって(最初は空間)データを任意の形式のクラスターに分割する問題の解決策として提案されました。 ほとんどのフラットパーティションアルゴリズムは、クラスターの中心までのドキュメントの距離を最小化するため、球状に近い形状のクラスターを作成します。 DBSCANの作成者は、彼らのアルゴリズムがさまざまな形状のクラスターを認識できることを実験的に示しました。
主なアイデア
アルゴリズムの根底にある考え方は、各クラスター内に典型的なポイントの密度(オブジェクト)があり、クラスターの外側の密度、および任意のクラスターの密度を下回るノイズがある領域の密度よりも著しく高いことです。 より正確には、各クラスターポイントについて、指定された半径の近傍には少なくとも特定の数のポイントが含まれている必要があり、このポイント数はしきい値によって指定されます。 アルゴリズムの基本的な特徴を詳細に説明するには、多くの定義を導入する必要があります-197-200ページの優れた学習ガイド[1]で、これらのアルゴリズムについて詳しく知ることができます。 著者が提案したアイデアの実装に直接注意を向けることをお勧めします。
入出力情報
入力は、次元nx 4のcont行列です。検討中のポイントの座標は最初の2列にあり、他の2列は0で埋められています。
アルゴリズムの結果として、contマトリックスの列3と4が埋められます。3番目の列は、ポイントが処理されたかどうかに関する情報を反映しています。 4列目は、1からs-1までの特定のクラスに属する役割を果たします。 4列目に-1が書き込まれている場合、このポイントはノイズに起因していました。
MATLABでの実装
n = length(cont(:,1)); %% L_min = 30; %% L = zeros(n,n); %% Rez = zeros(n,1); %% for i=1:1:n %% < L_min % L(:,i)=sqrt((cont(:,1)-cont(i,1)).^2 + (cont(:,2)-cont(i,2)).^2)<=L_min; %% < L_min % Rez(i) = sum(L(:,i))-1; L(:,i)=L(:,i).*(1:1:n)'; %% < L_min end kol=5; %% < L_min c=1; %% for i=1:1:n if cont(i,3) == 0 %% "" if Rez(i)<kol %% < L_min, cont(i,3)=1; %% "" cont(i,4)=-1; %% else %% < L_min, uvec = cont(:,4); %% cont(i,4)=c; %% while sum(uvec-cont(:,4))~=0 %% uvec = cont(:,4); %% for j=1:1:n %% if cont(j,4)==c && cont(j,3)==0 %% "" if Rez(j)<kol %% L_min kol cont(j,3)=1; %% cont(j,4)=-1; %% else %% cont(j,3)=1; %% "" cont(find(L(j,:)>0),4)=c; %% L_min end end; end; end; c=c+1; %% end; else continue end; end;
MATLABコードの強調表示が正しくないことをおpoび申し上げますが、HABRAHABRでは理解できませんでした。
作業結果
アルゴリズムの初期情報が、明確に区別された3つのグループに加えて、ノイズに起因する必要があるポイントを含むポイントのセット(下図を参照)であるとします。
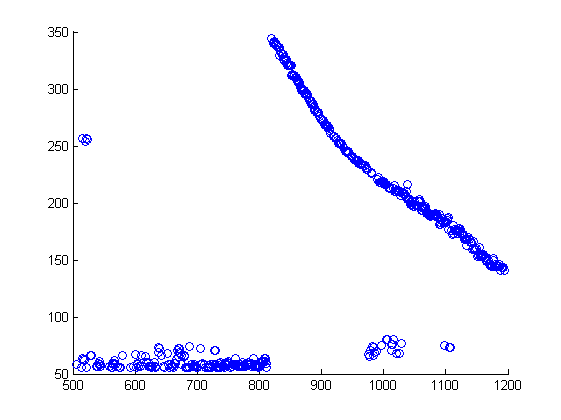
アルゴリズムが機能すると、次のクラスタリングの図が得られます。
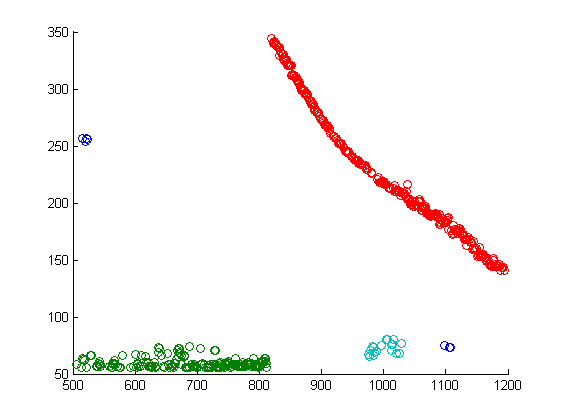
ご覧のように、アルゴリズムは3つのグループとノイズ(画像内の青い散乱)を識別しましたが、これは予想されていたものです! また、特定の曲線に沿って配置されたポイントを選択するタスクにアルゴリズムがうまく対処したという事実に読者の注意を喚起したいと思います。
文学
自然言語およびコンピューター言語学のテキストの自動処理:教科書。 手当/ Bolshakova E.I.、Klyshinsky E.S.、Lande D.V.、Noskov A.A.、Peskova O.V.、Yagunova E.V. -M .: MIEM、2011年-272 p。