このプロジェクトに参加したときに最初にしたことは、問題の本質、つまり解決したい問題を定式化することでした。 私が関わったほとんどすべてのプロジェクトで、計画は個々のタスクの正確な見積もり、タスクの期間、複雑さ、またはコストとして示された特定の数値に基づいていました。 少数のプロジェクトのみがPERT方法論を使用して、最も予想されるコストに加えて、楽観的および悲観的推定値を決定しましたが、この場合でも、プロジェクト全体の推定値は1つの特定の数値でした。 実際には、実際のコストは常に初期推定値よりも多かれ少なかれ、完全一致の確率はゼロになる傾向があることを理解しました。 割り当てられた予算は使い果たされるか、十分に活用されないと確信していました。 私たちの潜在的なクライアントと私は個人的に、特定の予算に収まる確率、つまり 一方では、プロジェクトの途中でお金がなくなる状況を回避し、他方では、既にビジネスに追加の利益をもたらすことなく単に「マスター」されているだけの過剰なお金がある状況を回避します。
そして、ここで私は幸運でした。世界最大のアウトソーシングサービスのプロバイダーの1つである当社は、完了したプロジェクトに関する膨大な量のデータを保有しており、ロシアのプロジェクトの1つから大量のデータをすばやく取得できました。 1〜50時間の一般的な人件費で、数千のアプリケーションの見積もりと実際のコストの値を取得しました。 Excelで簡単に操作した後、目的の分布が得られました(図1)。 ヒストグラムは、アプリケーションの数を垂直に示し、予測されたものに対する実際のコストを水平に示します。 たとえば、実際のコストが推定値と一致する場合、ヒストグラムでは、注文はポイント1の列で1単位増加します。実際のコストが半日で、推定値が2日間の場合、注文はポイント0.25になります。
図1 1つのプロジェクトでの実際のコストの分布

結果のグラフを分析したときに見たものは次のとおりです。
まず、従業員が非常に妥当な評価を行うことが判明しました。 確率が最大のコストを示します(このポイントはグラフ上で緑色でマークされています)。 一部のタスクに12時間かかるとスペシャリストが言う場合、タスクに正確に12時間かかる確率は、実際のコストが11または13時間になる確率よりもわずかに高く、コストが6または24時間になるという事実よりもはるかに高い。
第二に、すべてのアプリケーションの平均コストを計算すると、算術平均が最初の推定値よりも著しく大きいことがわかりました。 プロジェクトの最初の年に、平均コストは初期見積もりを50%超え、差は30%に減少しましたが、消えませんでした。 この一見奇妙な事実には簡単な説明がありました。 最初の評価よりもコストを削減する方向に間違いを犯すことはできません(コストのサイズは負の値にはできません)。また、推定値を超える方向にはほとんど制限がなく、実際のコストは推定値を2、3、4超えることができますまたは10回。 残念ながら、例が用意されています。 その結果、コストを増加させる方向のエラーは、減少する方向のエラーを上回り、平均すると、実際のコストは、もっともらしい推定値よりも大きくなります。 統計の言語では、実際のコストの分布は非対称であり、数学的な期待値は分布モードよりも大きいことがわかります。
次に重要な観察事項は、約束されたコストに収まることを保証する人々の行動です。 これを確認するために、彼らはそのコストの見積もりをサブスクライブし、そのリスクは5-10%以下です。 そして、これは、実際のコストが約束よりも低くなる確率が90〜95%であり、受け取った分布から判断すると、2〜3倍を超えることを意味します。 予算と期限の遵守を保証すると、予算と期限が2倍から3倍になります。 妥当性と現実性に関係なく、タイムラインと予算を厳密に制御することにより、全体的な効率の低下が保証されます 。
この影響に対処するために、一部の顧客および経営幹部は、最も可能性の高い費用の見積もりを目標として指定し、緊急準備金内の見積もりの超過の可能性を容認することを要求しています。 残念ながら、そのような予備のサイズが20%を超えることはめったになく、上で書いたように、個々のタスクのコストは平均でもっともらしい見積もりを30-50%超えています。 大規模プロジェクトのフレームワーク内で、個々のタスクのエラーは互いに補完できますが、それでも時間の経過とともにエラーが蓄積し、目標予算の超過が保証されます。
この有害な影響を克服するには、2つの方法のいずれかを使用できます:もっともらしい推定値の合計に対する補正係数を計算するか、ヘンリーフォードとフレデリックテイラーのアイデアに基づいて前世紀の50年代に開発されたPERTメソッドを使用できます。 最初の方法は簡単ですが、2番目の方法では、現実的な見積もりを取得できるだけでなく、実際のコストの可能な値の分布を理解することもできます。
***
補正係数を使用して、もっともらしいものに基づいて現実的な推定値を計算するには、この係数を最初に計算する必要があります。 これを行うには、少なくとも20〜40の完了したタスクを取り、実際のコストと初期見積もりの平均比率を計算します。 推定のサイズが2〜3倍以上異なる場合、異なるサイズのタスクに対して2、3、またはそれ以上の係数を決定することは理にかなっています。 使用したデータでは、推定2時間未満のタスクの補正係数は、推定12〜24時間のタスクの係数の3倍です。
補正係数のセットが取得された後、各妥当な推定値に対応する補正係数を乗算し、結果の積を要約する必要があります。 その結果、プロジェクトコストの現実的な推定値が得られます。これにより、サプライヤーが予算を超過するリスクは、顧客が余分に支払うリスクと等しくなります。
この方法の欠点は、結果が補正係数の計算精度に強く依存することです。そのため、この方法を使用するほとんどのアジャイル方法では、各反復またはリリース後に補正係数を更新する必要があります。 さらに、これらの方法論は、ほぼ同じサイズのタスクへの作業の内訳を促進し、1つの要素で管理できるようにします。
***
PERTメソッドは、前のメソッドとは異なり、事前定義された係数を使用せず、各タスクにいくつかの推定値を使用して、プロジェクト全体の現実的な推定値を計算します。
PERTメソッドを使用して現実的なプロジェクト推定値を計算するには、各タスクに対して3つの推定値を示す必要があります:通常の方法で得られる最も妥当な推定値、楽観的-タスクの複雑性を過大評価する場合の最小コストの評価、および悲観的-必要な最大コストの評価タスクを完了します。 その後、個々のタスクの現実的な評価は、以下の式で決定されます。 プロジェクト全体のコストは、各タスクの現実的な推定値の単純な合計によって推定されます。

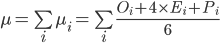
どこで
μ-プロジェクトまたはリリース全体のコストの現実的な見積もり、
nは、プロジェクトまたはリリース内のタスクの数です。
μi-タスクiの現実的なコスト見積もり、
O i-タスクiの楽観的なコスト見積もり、
E i-タスクiの最も可能性の高いコスト見積もり、
P i-タスクiの悲観的なコスト推定
ここで、得られたデータの別の特徴に注意を払うことが重要です-減少方向の半分の間違いの確率は、増加方向の半分の間違いの確率と等しいことが判明しました。 つまり (絶対誤差とは対照的に)相対誤差の分布は対称的であることが判明しました。 したがって、現実的推定値と楽観的推定値の比は、悲観的コスト推定値と現実的推定値の比と最小限に異なるか、等しくなければなりません。
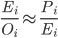
そうでない場合は、楽観的および悲観的推定の正確性を確認することは理にかなっています。
***
予期せぬニーズに必要な引当金を決定するには、特定の評価で考えられるコストの間隔を計算する必要があります(図2を参照)。 タスクの初期評価が16時間だった場合、50%の確率で、実際のコストは15〜24時間の範囲にあると言え、95%の確率では、コストは3〜56時間の範囲で。
図2.信頼区間
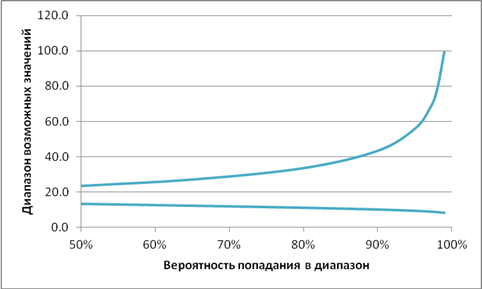
最も一般的なのは、90%の確率で範囲を使用することです。 この場合、コストは悲観的推定値を超え、コストは楽観的推定値よりも5%少ないと想定されます。 実際のコストが楽観的な見積もりと悲観的な見積もりの間に入る確率は90%です。
リリースおよびプロジェクトの実際のコストの確率分布を取得するには、PERT方法論で取得した楽観的および悲観的な推定値を使用します。 可能な値の範囲を取得するための方法論自体は、楽観的および悲観的な推定値を単純に加算することを示唆していますが、単純なモデリングはこれが間違っていることを示しています。 プロジェクトの悲観的な評価は、評価の合計よりも少ないことがわかりますが、楽観的な評価は大きくなります。 90%の確率の範囲は、個々のタスクの範囲の単純な合計よりも小さくなります。
必要なランダムに分布する値の範囲を計算するための正確な公式はありませんが、プロジェクトまたはリリース内のタスク数の平方根に比例して、可能なコスト値の広がりが大きくなるという次の公式により、適切な近似が与えられます:
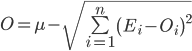
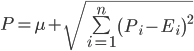
したがって、大規模なプロジェクトを細かく分割して個々のタスクをより深く考えるほど、より正確に見積もりを出すことができます。 たとえば、人件費が50,000 h-dayに達する大規模な統合実装プロジェクトを採用した場合、計画を1,000タスクに分割すると、理論的には800 h-dayまたは2%未満のエラーが発生します。 計画の詳細に応じたコストの広がりの理論的依存性のグラフを図3に示します。
図3 計画内のサブタスクの数に応じたコスト見積もりの精度の理論的依存性:
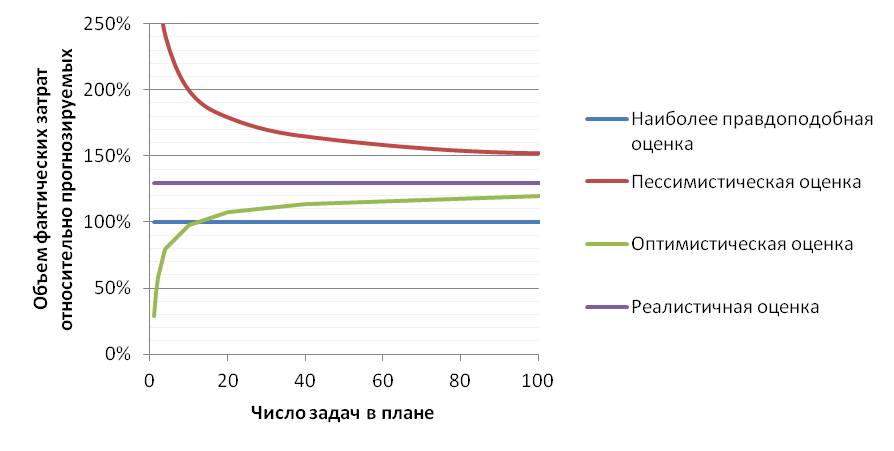
残念ながら、実際には、このような精度を達成できない多くの制限があり、最も重要なことは、実行されるタスクの要件と構成がプロジェクトの進行中に変更される可能性があることです。 ほとんどの企業では、通常、タスクの10〜30%の関連性が失われます。そのため、計画をどのように詳細化しても、初期見積もりの誤差は依然として避けられません。
調査結果を要約すると、次のことが理解できました。 最も妥当なコスト推定値の合計を使用して大規模プロジェクトを評価すると、推定値を過小評価し、悲観的な推定値を合計することが保証されます-高すぎることが保証されます。 現実的な推定値を取得するには、事前に計算された補正係数またはPERT推定手法を使用する必要があります。 PERT方法論の推定値を使用して、さまざまなコストを取得することもできます。これについては、実際のコストが90%の確率でそれに該当し、不必要な準備金がないと言えます。 また、プロジェクト計画を詳細に記述し、各タスクを正確に評価することにより、この範囲を大幅に縮小し、最終的に必要な埋蔵量を達成できます。