多くの人々は、予測不能性を作成したり、オブジェクトの動きや動作をより自然にしたり、テクスチャを生成したりするために、プログラムで乱数ジェネレーターを使用する必要がありました。 もちろん、乱数ジェネレーターには独自の応用分野がありますが、出力が「ハード」すぎて自然に見えない場合があります。 この記事では、私が考えていた以上に非常に幅広いアプリケーションを持つ関数を紹介しますが、ほとんどの場合、自然に見えるものが必要な場所です。 さらに、出力はニーズに合わせて簡単にカスタマイズできます。
自然界の多くのものを見ると、それらはフラクタルであることがわかります。 それらにはさまざまな詳細レベルがあります。 典型的な例は、山脈の輪郭です。 高さ(山)、中程度の変化(丘)、小さな変化(岩)、小さな変化(石)などの大きな違いが含まれています。 何でも見てください:フィールド上の草の斑点の広がり、海の波、アリの動き、木の枝の動き、大理石のパターン、風。 これらのすべての現象は、大小さまざまなバリエーションで同じパターンに役立ちます。 Perlinのノイズ関数は、さまざまなスケールでノイズ関数を単純に加算することでこれを再現します。
Perlinノイズ関数を作成するには、ノイズ関数と補間関数の2つが必要です。
ノイズ関数
ノイズ関数は、本質的に乱数ジェネレーターのサンプルです。 パラメータとして整数を受け取り、そのパラメータに基づいて乱数を返します。 同じパラメーターを2回渡すと、同じ数値が2回返されます。 彼女がこのように振る舞うことは非常に重要です。そうしないと、彼女からは何の意味もありません。
これはノイズ関数の例を示すグラフで、X軸上の各ポイントに0〜1のランダムな値が割り当てられています。
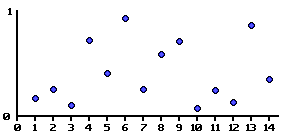
値間のスムーズな補間により、非整数をパラメーターとしてとる連続関数を決定できます。
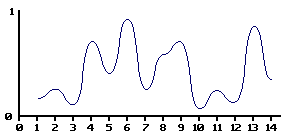
値を補間するさまざまな方法については、この記事の後半で説明します。
定義
先に進む前に、振幅と周波数の意味を決めてみましょう。 物理学を勉強していれば、正弦波に適用される振幅と周波数の概念に出くわしたかもしれません。
正弦波
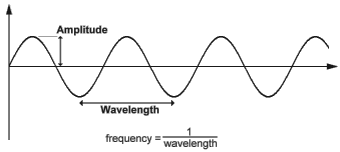
(振幅-振幅、波長-波長、周波数-周波数)
波長は、ある頂点から別の頂点までの距離です。 振幅は波の高さです。 周波数は1 /(波長)として定義されます。
ノイズ波
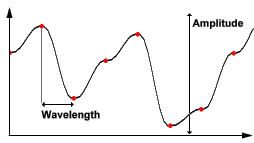
たとえば、このノイズ関数のグラフでは、赤い点は関数を測定することにより決定されるランダムな値を示します。
この場合、振幅は、関数が持つ可能性のある最小値と最大値の差です。 波長は、ある赤い点から別の点までの距離です。 繰り返しますが、周波数は1 /(波長)として定義されます。
パーリンノイズ関数の作成
さて、さまざまな周波数と振幅でこのような滑らかな関数をたくさん取った場合、それらをすべて加算してノイズの多い関数を作成できます。 これは、Perlinノイズの関数です。
次のノイズ機能を使用してください
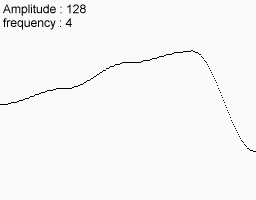
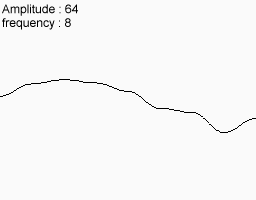
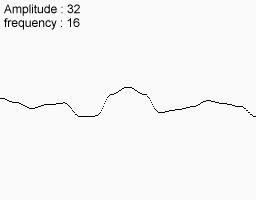
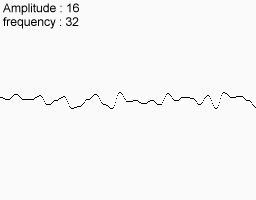
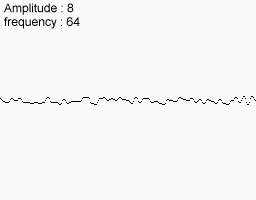
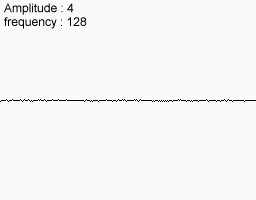
それらを一致させると、これが最終的に得られるものです。
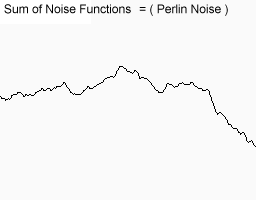
この関数には、大、中、小のバリエーションがあります。 山脈のように見えることも想像できます。 実際、多くのコンピューターランドスケープはこの方法を使用して作成されています。 もちろん、彼らは私が現時点で受け取った2Dノイズを使用しています。
もちろん、2次元でも同じことができます。 2Dのいくつかのノイズ機能






これらの機能をすべて追加すると、ノイズ画像が得られます。

持続性
これらのノイズ関数を一緒に追加すると、それぞれがどのような振幅と周波数を使用するのか疑問に思うかもしれません。 1次元の例では、周波数の2倍と振幅の半分が、後続の各追加ノイズ関数に使用されました。 これはかなり一般的な出来事です。 したがって、実際には、多くの人は他のすべてを使用することさえ考えていません。 ただし、ステップごとに異なる特性と異なる周波数と振幅を使用して、perlin関数のノイズを作成できます。 たとえば、滑らかな丘を作成するには、低周波数では振幅が大きく、高周波数では振幅が非常に小さいPerlinノイズ関数を使用できます。 または、低周波数用に小さな振幅を選択することにより、平らではあるが非常に岩の多い平面を作成できます。
これをより簡単に説明し、「振幅」と「周波数」という言葉を常に繰り返すことを避けるために、単一の数値を使用して各振幅と各周波数を決定します。 この値は永続性と呼ばれます。 正確な意味については不確実性があります。 この用語は元々、フラクタルの発見の背後にいる人の一人であるマンデルブロによって造られました。 彼は、低抵抗の高周波数のノイズを特定しました。 私の友人のMattも忍耐の概念を思いつきましたが、それを逆に定義しました。 正直なところ、私はマットの定義を好みます。
申し訳ありませんが、マンデルブロ。
したがって、忍耐力の定義は次のとおりです。
frequency() = 2^i amplitude() = persistence()^i
ここで、iはi番目の追加ノイズ関数です。
パーリンノイズ出力に対する永続性の効果を説明するには、以下の図をご覧ください。
これらは、追加された関数のノイズ成分、値を保存する効果、そして結果として、Perlinノイズ関数を示します。
耐久性= 1/4
頻度:1、2、4、8、16、32
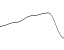




 =
= 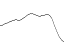
振幅:1、1 / 4、1 / 16、1 / 64、1 / 256、1 / 1024
耐久性= 1/2
頻度:1、2、4、8、16、32
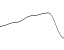


 =
= 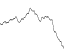
振幅:1、1 / 2、1 / 4、1 / 8、1 / 16、1 / 32
耐久性= 1 / root2
頻度:1、2、4、8、16、32
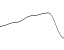


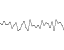
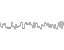
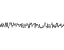 =
= 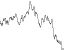
振幅:1、1 / 1.414、1/2、1 / 2.828、1/4、1 / 5.656
耐久性= 1
頻度:1、2、4、8、16、32
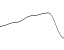

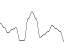
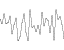

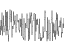 =
= 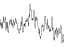
振幅:1、1、1、1、1、1、1
オクターブ
追加される後続のノイズ関数はそれぞれオクターブと呼ばれます。 これは、各ノイズ関数の周波数が前の関数の2倍であるためです。 音楽では、オクターブもこの特性を備えています。
追加するオクターブの数は完全にあなた次第です。 必要な数だけ追加することも、いくつか追加することもできます。 ただし、いくつかアドバイスをさせてください。 Perlinのノイズ関数を使用して画面に画像をレンダリングすると、オクターブの周波数が高すぎて表示できない場合があります。 非常に高いノイズ関数ですべての詳細を再現するのに十分なピクセルが画面上にない場合があります。 Perlinノイズの一部の実装では、画面解像度(または他の媒体)の制限に達するまで、自動的にノイズ関数が加算されます。
さらに、結果に影響を与えるには振幅が小さくなりすぎたときにノイズ関数を追加するときに停止するのが賢明です。 正確にこれが起こるときは、抵抗のレベル、Perlin関数の一般的な振幅、および画面解像度のビット(または他の何か)に依存します。
ノイズ関数を作成する
ノイズ関数で何を探していますか? 本質的には乱数ジェネレーター。 ただし、呼び出すたびに異なる乱数を与えるプログラムで遭遇する他の乱数ジェネレーターとは異なり、これらのノイズ関数は1つ以上のパラメーターから計算された乱数を生成します。 つまり、同じ番号を入力するたびに、ノイズ関数はこの番号に対して以前と同じ番号で応答します。 しかし、別の番号を入力すると、別の番号が返されます。
まあ、私は乱数ジェネレーターについてあまり知らないので、探し始めました、そして、ここでそれを見つけました。 彼はかなり良さそうでした。 -1.0〜1.0の浮動小数点数を返します。
function IntNoise(32-bit integer: x) x = (x<<13) ^ x; return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end IntNoise function
さて、おそらくいくつかの異なる乱数ジェネレーターが必要になるので、上記のコードのいくつかのコピーを作成することをお勧めしますが、わずかに異なる数を使用します。 これらの大きくて不気味な数字はすべて素数なので、同じサイズの他の素数を使用できます。 したがって、乱数を見つけやすくするために、素数をリストする小さなプログラムを作成しました。 彼女に開始番号と終了番号を与えると、彼女はそれらの間のすべての素数を見つけます。 ソースコードも含まれているため、プログラムに簡単に組み込んで、ランダムな素数( プログラムとコード )を作成できます。
( リソースに負担をかけないために、ここにコードを完全に投稿します。あまり多くはないので )
#include <stdlib.h> #include <iostream.h> #include <math.h> inline long sqrt(long i) { long r,rnew=1,rold=r; do { rold=r; r=rnew; rnew = (r+(i/r)); rnew >>= 1; } while(rold != rnew); return rnew; } inline int isprime(long i) { long si,j; si = sqrt(i); for (j=2; (j<=si); j++) { if (i%j == 0) return 0; } return 1; } void main(int argc, char *argv[]) { long i,i1,i2,f=0; if (argc < 2) { cout << endl << endl; cout << "Prime number finder: Hugo Elias 1998" << endl << "http://freespace.virgin.net/hugo.elias" << endl << endl; cout << "Usage:" << endl << " primes ab > primes.txt" << endl << endl; cout << "will find all primes between a and b" << endl << "and will write the results to the file PRIMES.TXT" << endl; return; } i1 = atol(argv[1]); i2 = atol(argv[2]); for (i=i1; i<i2; i++) if (isprime(i)) { f++; if (f==16) { cout << endl; f=0; } cout << i << " "; } }
補間
ノイズ関数を作成したら、それが返す値を平滑化する必要があります。 繰り返しますが、好きな方法を選択できますが、一部は他の方法よりも良く見えます。 標準の補間関数には、3つの入力a、b、それらの間の補間値、および0〜1の値を取るxがあります。補間関数は、xの値に応じてaとbの間の値を返します。 xが0の場合、aが返され、x = 1の場合、bが返されます。 xが0と1の間の場合、aとbの間の値を返します。
線形補間
多くの人が風景を作成するために使用する安価な「プラズマ」のように、それはひどく見えます。 ただし、これは単純なアルゴリズムであり、Perlinのノイズをリアルタイムで生成しようとした場合、それは許されると思います。
function Linear_Interpolate(a, b, x) return a*(1-x) + b*x end of function

コサイン補間
この方法では、線形補間よりも滑らかな曲線が得られます。 これは明らかに最高の結果であり、速度の低下が非常に小さい場合は努力する価値があります。
function Cosine_Interpolate(a, b, x) ft = x * 3.1415927 f = (1 - cos(ft)) * .5 return a*(1-f) + b*f end of function

キュービック補間
この方法では非常にスムーズな結果が得られますが、その代価は迅速に支払われます。 正直なところ、これがコサイン補間よりもはるかに良い結果をもたらすかどうかはわかりませんが、ここではいずれにしてもあなたの裁量です。 これは少し複雑なので、注意してください。 以前に、補間関数に3つの入力があった場合、3次補間には5が必要です。 aとbの代わりに、以前と同様に、v0、v1、v2、v3とxが必要になりました。

v0 =ポイント
v1 =ポイントa
v2 =ポイントb
v3 = bの後のポイント
function Cubic_Interpolate(v0, v1, v2, v3,x) P = (v3 - v2) - (v0 - v1) Q = (v0 - v1) - P R = v2 - v0 S = v1 return Px3 + Qx2 + Rx + S end of function

滑らかなノイズ
補間に加えて、ノイズ関数の出力を平滑化して、2Dおよび3Dバージョンの領域を小さくするだけでなく、ランダム性を低くすることもできます。 スムージングはあなたが期待する以上のことをします。そして、スムージングフィルターや発火アルゴリズムを書いた人は誰でもこのプロセスに慣れているはずです。 座標の1つでノイズ関数の値を取得する代わりに、この値と隣接する座標の値の平均を取得できます。 これが明確でない場合は、以下の擬似コードをご覧ください。
小さな図では、平滑化されたノイズ関数と平滑化されていない同じノイズ関数の違いが示されています。
滑らかなノイズ関数が滑らかになり、滑らかでないノイズ関数の極値に達することはなく、周波数は約半分であることがわかります。 これが実際に唯一の効果であるため、1次元ノイズを平滑化することにはほとんど意味がありません。 平滑化は、2次元または3次元でより有効になります。効果は、ノイズの直角度を減らすことです。
残念ながら、これによりコントラストも低下します。 滑らかにすればするほど、ノイズは明らかに平坦になります。



1次元の平滑化ノイズ
function Noise(x) . . end function function SmoothNoise_1D(x) return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4 end function
2次元の平滑化ノイズ
function Noise(x, y) . . end function function SmoothNoise_2D(x>, y) corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16 sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8 center = Noise(x, y) / 4 return corners + sides + center end function
すべてをまとめる
これですべてがわかったので、学習したすべてをまとめて、Perlinノイズ関数を作成します。 これらはノイズ関数補間のほんの数個の追加であることに注意してください。 したがって、Perlinのノイズは単なる関数です。 1つ以上のパラメーターを渡すと、数字で応答します。
したがって、ここに単純な1次元のPerlin関数があります。 Perlinの機能の主要部分はループです。 ループを繰り返すたびに、2倍の周波数でオクターブが追加されます。 各反復は、ノイズiで示される異なるノイズ関数を呼び出します。 擬似コードで想定されているように、オクターブごとに1つずつ、多くのノイズ関数を記述する必要はありません。 これら3つの大きな素数の意味を除いて、すべてのノイズ関数はほぼ同じであるため、同じコードを保持できますが、それぞれに対して異なる素数のセットを使用するだけです。
1次元のパーリンノイズ(擬似コード)
function Noise1(integer x) x = (x<<13) ^ x; return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end function function SmoothedNoise_1(float x) return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4 end function function InterpolatedNoise_1(float x) integer_X = int(x) fractional_X = x - integer_X v1 = SmoothedNoise1(integer_X) v2 = SmoothedNoise1(integer_X + 1) return Interpolate(v1 , v2 , fractional_X) end function function PerlinNoise_1D(float x) total = 0 p = persistence n = Number_Of_Octaves - 1 loop i from 0 to n frequency = 2i amplitude = pi total = total + InterpolatedNoisei(x * frequency) * amplitude end of i loop return total end function
同じコードを簡単に適用して、2次元以上のPerlinノイズ関数を作成できるようになりました。
2次元のパーリンノイズ(擬似コード)
function Noise1(integer x, integer y) n = x + y * 57 n = (n<<13) ^ n; return ( 1.0 - ( (n * (n * n * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end function function SmoothNoise_1(float x, float y) corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16 sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8 center = Noise(x, y) / 4 return corners + sides + center end function function InterpolatedNoise_1(float x, float y) integer_X = int(x) fractional_X = x - integer_X integer_Y = int(y) fractional_Y = y - integer_Y v1 = SmoothedNoise1(integer_X, integer_Y) v2 = SmoothedNoise1(integer_X + 1, integer_Y) v3 = SmoothedNoise1(integer_X, integer_Y + 1) v4 = SmoothedNoise1(integer_X + 1, integer_Y + 1) i1 = Interpolate(v1 , v2 , fractional_X) i2 = Interpolate(v3 , v4 , fractional_X) return Interpolate(i1 , i2 , fractional_Y) end function function PerlinNoise_2D(float x, float y) total = 0 p = persistence n = Number_Of_Octaves - 1 loop i from 0 to n frequency = 2i amplitude = pi total = total + InterpolatedNoisei(x * frequency, y * frequency) * amplitude end of i loop return total end function
元の記事の最後に、興味深い資料が追加されていますが、これを読むのは難しくないと思います。
参照:
実際には記事自体 。
Ken PerlinのWebサイト
ps:親愛なるマイナスの人々、マイナスの動機付けはすでに受け入れられていませんか?