そして、私たちはすでに持っています:
通常の長方形グリッドで検索します。
必要なもの:
最小限の労力で六角形のグリッドを検索します。
一般的なグリッド構造
最初のアイデアは、列全体を単純にシフトすることです。
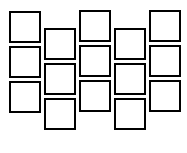
次に、現在のセルの隣は次のようになります。
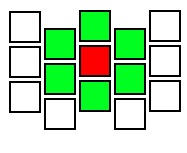
ご覧のように、理論上、セル間の接続は16進数になります。
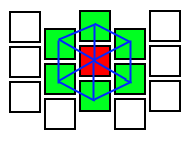
しかし、すぐには疑念が忍び寄ってきます。正方形はまったくなく、長方形があるはずです。
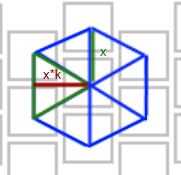
図のkを計算することは難しくありません。sqrt(3)/ 2に等しくなります
その結果、グリッドが得られます
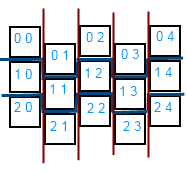
各セルのサイズは、それぞれw = sqrt(3)/ 2、h = 1であり、各奇数列(0からカウントを開始する場合)は0.5シフトされます。
座標変換
その後、すべてが簡単になり、偶数/奇数列に調整された座標をセル番号に変換します。
(x,y)=>(x/w, (y-(x/w)%2)/h)
それどころか、フィールドセルを座標に変換します。
(i,k)=>(i*w, k*h+h/2*(i%2))
隣人
次に、選択したセルのすべての隣接セルを取得する必要があります。
偶数列ではこのようになります(奇数列では対称になります)。
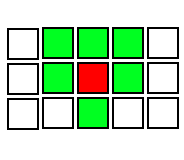
(i,k)=>(
(i+1,k),
(i-1,k),
(i,k+1),
(I,k-1),
(i+1,k+(1-2*i%2)),
(i-1,k+(1-2*i%2)))
2つのセル間の距離
さて、本格的な実装では、2つのセル間の距離を見つける方法だけが欠けています。もちろん、簡単なユークリッドを使用できますが、これは私たちのオプションではありません。 基本的には、通常のグリッドで対角距離を取ります。
xd = abs(p1.X - p2.X);
yd = abs(p1.Y - p2.Y);
diagonal = min(xd, yd);
straight = xd + yd;
result = sqrt(2) * diagonal + (straight - (2 * diagonal)));
私たちの状況は似ています(斜めの動きもあります)、垂直にシフトするだけです(例のようにグリッドの向きを考慮して)、垂直に1歩または水平に2歩を取ることができます。
//
if (xd >= yd * 2)
{
result = xd;
}
//
else
{
result = xd + (yd – xd/2);
}
ただし、ここで少し詳しく説明します。異なる列の2つのセルの間の距離を測定すると、セルの床への不明な変位が生じます。 したがって、ydは少し異なる方法で定義する必要があります。
yd =abs((p1.Y + (p1.X%2)/2) – (p2.Y + (p2.X%2)/2));
ここで、たとえば、 ここで行ったように、すべてにA *を設定します 。
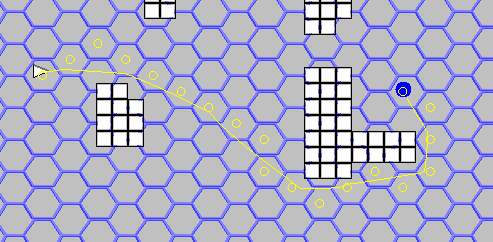
あとがきの代わりに
もちろん、六角形のグリッドを操作するためのより美しい数学的な方法がありますが、私の意見では、この方法は生きる権利を得るのに十分なほど簡単であることが判明しました(そしてパフォーマンステストのプラスはかなり良い結果を示しました)。