無臭フィルタリングと非線形推定*

*英語から 「無香フィルターと非線形推定」（by Google Translate ）

dmitriynの要求に応じて、彼はいわゆる「Unscented Kalman filter」に関するビジョンを発表することを決定しました。これは、線形カルマンフィルタリングを、ダイナミクスの方程式とシステムの観測が非線形で適切に線形化できない場合に拡張したものです。

このフィルタリング方法の名前は「コーシャ」であるため 、ロシア語で読めるため、記事のタイトルに何が反映されているのかわかりません。そこで、かなり面白い機械翻訳をコピーして貼り付けることにしました。 翻訳の別の楽しいバージョンは、 ファジーフィルターです。


UPD ：セクション「USING UT」にコメントを追加

はじめに

線形カルマンフィルタリングに関する以前の記事では、動的システムの線形化された単純化された数学モデルの場合について、フォトニック結晶の合成への可能なアプローチの1つが説明されました。 そこで説明されているカルマンフィルターは、文献では「従来のカルマンフィルター」と呼ばれることがあります[ 2 ]。 彼はこの名前を受け取りました いくつかの仮説（慣習）が観察される場合にのみ最小の二乗平均平方根誤差が得られます-たとえば、ノイズが白であり、通常の法則に従って分布している、ノイズの期待値がゼロである、ノイズと位相座標間の相互接続の間に相関がない場合 これらの制限は非常に深刻であり、実際には多くの場合、仮説に違反しています。 これらの制限を回避できる手法があります（たとえば、色ノイズジェネレーターの座標フィルターを位相ベクトルフィルターに追加し、「シフトした」ノイズに架空の外乱を導入する）。 それらはすべて、計算の複雑さの増加（問題の次元が増大している）につながり、慣例に違反しないフィルターの合成が困難になります。

「拡張カルマンフィルター」[ 1 ]もあります。これは、構造が線形バージョンに似ており、ダイナミクスと観測の方程式に位相座標の非線形（パワー、三角関数など）関数が含まれていることを特徴としています（下の方程式を参照）。 この違いは、位相座標（たとえば、2つの座標の積）間の架橋の存在も意味します。









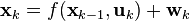
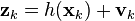
EKFを使用する場合、反復の各ステップで、位相座標の偏微分の行列であるヤコビアンを計算する必要があります。 このため、計算の複雑さが大幅に増加し、離散化された微分方程式の安定性の問題がさらに急激に発生します。 本質的に、EK​​Fは非線形力学系の線形化の層を実装します。 これが、EKFが無効になる主な理由です。 動的システムの強く非線形なモデルを使用すると、問題の条件が非常に悪くなります。 パラメータマットの設定における小さなエラー。 モデルは大きな計算エラーにつながります。 その結果、アルゴリズムは堅牢性（エラーに対する耐性）を失います。



無香料カルマンフィルター（UKF）[ 3 ]は、異なるアプローチ（「無香変換」）を使用します。 ウィキペディアによると、このアプローチは、ランダムノイズが重畳された目的のベクトルの期待値と共分散のデータに対して、特定の最小限のサンプルセット（シグマポイント）を選択することを意味します。 シグマポイントを使用して、非線形予測関数が構築され、これを使用して相互共分散行列（カルマンフィルタリングアルゴリズムのカーネル）が計算されます。

最後の段落を書いた後、私は個人的にさらに質問がありました。 彼が時間について尋ねられるまで、何時だったかを知っていた聖オーガスティンのように。 以下では、読者の皆さん、検討中の非線形フィルタリング法の本質を自分自身とあなたに明確にしようとします。

無香の変換

おそらく、線形カルマンフィルター（FC）と非線形（拡張、EKF）の2つの主な問題の詳細な説明から始めましょう。 最初の問題は干渉の慣習です。 前述のように、線形FCは、ノイズが「ホワイト」であり、通常の法則に従って分布していると想定しています。 ノイズが「色付き」の場合、「ホワイト」ノイズを通過させる際に、デジタルシェーピングフィルターを合成する必要があります。これにより、スペクトル特性が（理想的に）同等または既存の事実に近いノイズが得られます。 このフィルターの位相ベクトルは、FCの位相ベクトルに追加されます。 これにより、問題の次元が大きくなります。 この問題はそれほど深刻ではないと仮定します。 しかし、2つ目があります-数学モデルの非線形性の問題です。 非線形性のため、非線形行列関数を線形化できる近似器を実装する必要があり（上記の方程式の "h"を参照）、変数を分離する機能を提供します。 変数は、位相ベクトルの成分の方程式を作成できるように分離する必要があります。 EKFでは、線形化はヤコビアンを計算することによって実行されます。 「h」の各方程式について、偏微分が各位相変数に対して計算されます。 この操作自体はすでに問題です-大量の計算。 さらに、ヤコビアンの計算には、次の形式のテイラー級数展開（多次元）が使用されます。







この場合、シリーズの最初のメンバーのみが取得され、残りは無視できると見なされます。 したがって、この線形化を使用して、次の形式の式を取得します。





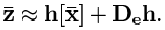
この方程式では、「De」は行列関数の全微分を計算する演算子です。



数学モデルの非線形性が小さい（モデルがほぼ線形である）場合、このステートメントは真であると見なすことができます。 ただし、実際には、モデルの非線形性は、2次および/またはそれ以上の小さの拡張項の破棄を許可しないようなものです。 このような場合、EKFでの線形化は計算エラーを生成しますが、これは無視できません。 特定のケースでは、テイラー級数に展開せずに行うことができますが、これらは特定のオブジェクトに厳密に結び付けられた特定のソリューションです。 また、テイラー級数を小さの2次項に切り捨てるソリューションもあります[6]。 これには、二次導関数のテンソルであるヘッセ行列の計算が含まれます。 ただ、私にそれが何であるかを噛ませないでください。 これにより、EKFがより困難になり、実装が複雑になることを理解するのに十分です。

したがって、位相ベクトルの現在の値を予測（「非線形」予測）して次の反復ステップに使用できる特定の変換がわかっている場合、FCをオブジェクトの非線形モデルに適用できます。 そのような（適切な）変換が不明な場合、EKFを使用します。EKFは、しばしば不適切な線形化と非常に大きな計算負荷を伴います。 したがって、EKFで使用される線形化なしで実行でき、EKFに比べて計算量が多くない方法が必要です。 この方法は無香変換です（UT、この略語をコンピューターゲームとさらに混同しないでください）。



UTの主なアイデアは、任意の非線形変換関数を近似するよりも、非ゼロの期待値（位相ベクトル-ランダムノイズが重畳されている）で確率変数の確率分布関数を近似する方がはるかに簡単であるという直感的な仮定の下で、 より多くのフラグメントを収集することです。 この手法は、パラメータ空間（位相座標）内の一連のポイント（シグマポイント）を特別な方法で選択することを意味し、十分な精度で、目的のランダムベクトル（この場合、位相ベクトルノイズベクトルが重畳されます）。 これらのポイントを選択するには、フォームの式が使用されます。





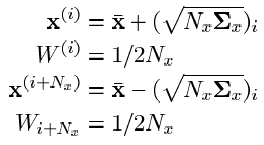
これらの式で、「 Nx 」は目的の位相ベクトルの次元です。 「 i 」はシグマポイントのインデックスです（i = 1 .. Nx ）。 「 Wi 」はi番目のシグマポイントの重みです。

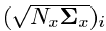-モデルの初期非線形変換の共分散行列の行列平方根のi番目の列に位相ベクトルの次元を掛けたもの。



これがシグマポイントのセットの唯一のオプションではないことに注意してください。 上記の式は、1番目と2番目の瞬間（期待値と分散）のみの分布統計を一意に特徴づけます。 高次のモーメントまでの所望のベクトルの分布の統計を特徴付けるUTは、シグマポイントの数（一般的に言えば、その数は必ずしも上記の式よりも大きくなるわけではありません）と重みの選択が異なります。 簡単にするために、詳細は省略します。 位相ベクトルの分布の統計の高次モーメントを考慮に入れて、UTの式を例としてのみ示します。





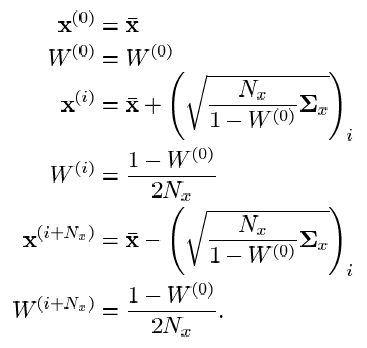
原則として、UT自体について、要するに、すべて。 なぜそれが必要であり、UKFでどのように使用されるかを以下に示します。 高次の瞬間の特性については予約する必要があります。 これは何ですか 直感的な例えは、動体の位置、速度、加速度です。 位置を1次モーメントと考えると、速度は2モーメント（位置の変化率）、加速度は3角（速度の変化率）になります。 加速度の導関数を計算できます-4番目の瞬間を取得します。 しかし、それは実用的な意味がありますか？ 同様に、統計のモーメント特性でも-ほとんどの場合、期待値と分散で十分です。 UTの統計的精度から、すなわち フィルタリング効率はシグマポイントの選択方法に依存しますが、ほとんどの実際的な問題では、高次のモーメント特性を考慮する必要がありました。

UTアプリケーション

前述のように、UTは非線形確率推定の線形化手順を取り除くことができる方法です。 これまでのところ、UTの助けを借りて、目的のベクトル（位相ベクトル）の統計を正確に特徴付けるポイントのセットを選択できることだけを学びました。 これにより何が得られますか？ カルマンフィルター処理の重要なポイントは、相互共分散行列の計算です（ 前の記事の Kk行列を参照 ）。 線形FCのこの行列は、行列Riccati方程式の解として計算されます。 非線形マットの場合。 システムモデルでは、この手順は非常に複雑です。 UTを使用すると、別の方法で相互共分散行列を取得できます。 以下は、UTメソッドを使用した段階的なフィルタリング手順です。

1. 目的のベクトル（位相ベクトルまたは観測ベクトル-センサーの出力信号のベクトル）の統計パラメーターを見つけます。 得られた統計特性は、一定であると見なされるか、リアルタイムで更新されます。
2. 取得した統計に基づいて、シグマポイントのセットを計算します。
3. これらの点を元の非線形マットに通します。 動的プロセスモデル：
   
   
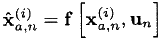
4. 予想と共分散の予測を計算します。
   
   
   
   
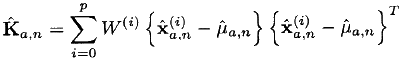
5. 3番目のステップで取得したポイントを観測モデルに渡します（一般的な場合、非線形）：
   
   
6. 観測の予測を計算します（前のステップの値の加重平均の形式で）：
   
   
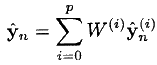
7. 観測の共分散を計算します。
   
   
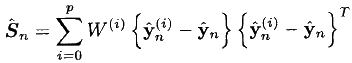
8. 必要な相互共分散行列を見つけます：
   
   
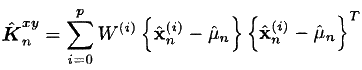
9. 最後に、標準のFC式を使用します。
   
   

式の最後のブロックは、記事[3]からそのままコピーされます。 私の意見では、彼女には何か問題があります。 kryzhaのない「yn」と識別マークのない相互共分散行列がどこから来たのかは不明です。 しかし、それは問題ではありません。 「FCの標準表現」については、すでに書きました。 必要なことは、カルマンのUTで見つかった行列ゲインを（相互共分散行列とも呼ばれる）に置き換え、位相ベクトルの修正された推定値を計算することだけです。

位相ベクトルについてもう1つ説明します。 上記の式には、インデックス「a」（Xa、n）の位相ベクトルがあります-これは、プロセスおよび観測ノイズの（拡張された）座標で補完された位相ベクトルです。 冒頭で、干渉のスペクトル特性に対する制限を回避するためのそのような手法があることを書きました。 そのため、上記の式では、拡張ベクトルから通常ベクトルへの移行は何となく静かに行われます（単純で拡張された「ミュー」期待もあります）。

結論

そのため、UTの助けを借りて、線形化することなく、位相ベクトルと相互共分散行列の予測を計算することができました。 FC予測の補正フェーズの標準式にそれらの値を代入して（線形FCに関する記事の「測定の更新」を参照）、位相ベクトルの推定値を取得しました。 この場合、最もリソースを消費する手順は、シグマポイントのセットの形成における行列の平方根の計算です。 UKFの全体的な複雑さは、EKFの複雑さ以上ではありません。 UKFの主な利点は、さまざまなタスクに対する合成の一般性（合成手順は使用するオブジェクトに依存しません）、および結果のアルゴリズムの安定性（UTの数値条件性はEKFの線形化手順の条件性よりも高い）と得られた推定値のバイアスがないことです（これにより、線形化の拒否）。 例として、記事[3]から推定誤差のグラフを示します（図1を参照）。



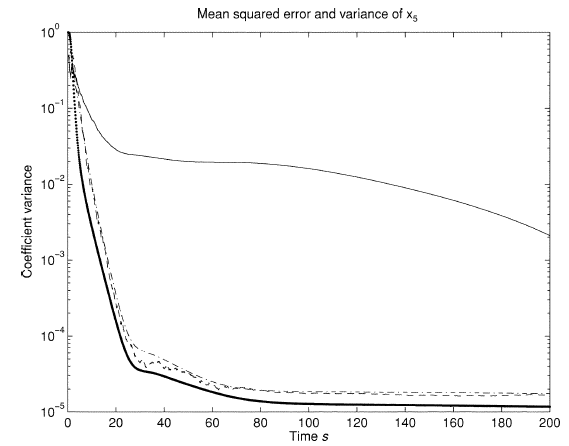
図 1. EKFおよびUKFのRMSエラーおよび推定分散プロット

この図では、細い線はEKFの平均二乗誤差（平均二乗誤差）です。 散布図（一番下の太字）-推定された共分散。 他の2つのグラフはUKFのものです。 EKFの共分散スコアは低くなります（多少滑らかになります）が、スコアのRMSEは非常に高くなります。 UKF共分散と標準偏差はほぼ同じレベルです。 ちなみに、ある種の間違いがあるように思えました。 分散は標準偏差の二乗です。 どうやって一緒にいることができますか？ ここで、上記の括弧で引用されている用語を誤って解釈したか、それにもかかわらず、共分散と標準偏差の推定値は別々です。

UPDまた、この方法がどのように機能するか、そしてその本質を正しく理解したかどうか、私自身はまだ完全に理解していないことに注意したい。 私はそれを実装しようとします-それは実装するのは本当に簡単なアルゴリズムのようです。 彼がどのように自分自身を見せてくれるか、時間はどうなるかを見る。

それまでの間、ご意見、ご提案、コメント...そしてご清聴ありがとうございました！

参考文献：

1. WikiのUKF
2. 非線形シグマポイントカルマンフィルターを使用した軌道決定に関する議論
3. ジュリアー、SJ; Uhlmann、JK（1997）。 「カルマンフィルターの非線形システムへの新しい拡張。」 Int。 シンプ 航空宇宙/防衛センシング、Simul。 およびコントロール3. 2008-05-03を取得。
4. ファジィ強力追跡無香料カルマンフィルター
5. 無香の変換
6. M.アサンズ、RPウィシュナー、およびA.ベルトリーニ、「準最適状態
   
   離散時間からの連続時間非線形システムの推定
   
   ノイズの多い測定、” IEEE Trans。 オートマトン。 Contr。、Vol。 AC-13、
   
   pp。 504-518、10月 1968年。