フーリエ変換を使用した多項式の高速乗算は簡単です

こんばんは

この投稿は高速フーリエ変換についてです。 （複素数での）直接および逆変換が考慮されます。 次のパートでは、olympiadプログラミングの問題（特に、文字列の「類似性」に関する1つの問題）でのアプリケーションの検討と、整数での変換の実装について説明する予定です。

FFTは、時間O （n⋅log n ）のnポイントで次数n = 2 ^kの多項式の値を計算するアルゴリズムです（「ナイーブ」メソッドは時間O （ n ² ）で同じタスクを実行します）。 同時に、逆変換を実行できます。 数値の配列の加算、減算、乗算は多項式よりもはるかに簡単なので（特に乗算）、FFTは多項式と長い数値を使用した計算を高速化するためによく使用されます。

定義と用途

まず、多項式とは何かを定義しましょう。

P （ x ）= a ₀ + x a ₁ + x ² a ₂ + x ³ a ₃ + ... + x ^{n - 1} a _{n - 1}

複素数

複素数に精通している場合は、この点をスキップできます。そうでない場合は、簡単な定義を以下に示します。

x = a + i b 、ここでi ² = -1

ここで、aは実部（ Real ）部と呼ばれ、 bは虚部（ Imaginary ）部です。 ご覧のとおり、これらの数から負の（そして実際に）数から根を抽出することができます-これは多項式を扱う場合に非常に便利です-代数の主定理から、 ）

平面上の点の形でそれらを表現することも非常に便利です。



複素数のもう1つの注目すべき特性は、 x =（cosα+ isinα） rで表現できることです。ここで、αは「数値」の極角（ 引数と呼ばれます ）、 rはゼロからそれまでの距離（ モジュラス ）です。 そして、2つの数字を掛けるとき：

a =（cosα+ i⋅sinα） r _a

b =（cosβ+ i⋅sinβ） r _b

a b =（cosα+ i⋅sinα）（cosβ+ i⋅sinβ） r _a r _b

a b =（cosα⋅cosβ-sinα⋅sinβ+ i （sinα⋅cosβ+cosβ⋅sinα）） r _a r _b

a b =（cos（α+β）+ i⋅sin（α+β）） r _a r _b

モジュールが乗算され、引数が追加されます。

1の複雑な根

次に、 1からのn次の複雑な根がどのように見えるかを理解しましょう。 x ⁿ = 1とすると、そのモジュールは明らかに1に等しく、n⋅argx = 2πk、ここでkは整数です。 これは、 nがそれ自体に数を乗算した後（つまり、 n乗）、その引数が「複数」2π（360度）になることを意味します。

引数とモジュールがわかっている場合、数値の式を思い出してください。

α= 2π⋅x / n 、ここで0 x

ωi =cosα+ i⋅sinα

つまり 描画すると、等間隔で円上の点のみが得られます。



積極的に使用する3つの点に注意してください（これらがないと、何も機能しません）。

ωa⋅ωb =ω <sub>（ a + b ）mod n

ω0</sub> +ω1 +ω2 + ... +ωn _{- 1} = 0

_ω0 ^{n / 2} =ω2 ^{n / 2} =ω4 ^{n / 2} = ... = 1 （偶数nの場合 ）

これらの特性のため、これらのポイントで多項式の値を検討します。 もちろん、結果は必ずしも現実のものではないため、プログラムは複素数を扱う必要があります。

根の合計がゼロである理由

証明は非常に簡単です：letφ= _ω0 +ω1 + .... 両側にω1（！= 1）を掛けます。 なぜなら ωi⋅ω1 =ωi _{+ 1} 、次にφ⋅ω1 =ω1 +ω2 + ... +ωn _{- 1} + _ω0 。 項の再配置から、合計は変化しないため、それぞれφ=φ⋅ω1、φ⋅（ω1-1）= 0です。 なぜなら ω1！= 1、次にφ= 0 。

仕組み

多項式の次数はn = 2 ^kであると仮定します。 そうでない場合は、先行する係数をゼロで最も近い2のべき乗で補います。

FFTの基本的な考え方は非常に簡単です。

させてください：

A （ x ）= a ₀ + x a ₂ + x ² a ₄ + ... + x ^{n / 2-1} a _{n - 2} （偶数の係数P ）

B （ x ）= a ₁ + x a ₃ + x ² a ₅ + ... + x ^{n / 2-1} a _{n - 1} （奇数係数P ）

次に、 P （ x ）= A （ x ² ）+ x⋅B（ x ² ）。

ここで、「分割征服」の原理を適用します。n点（ _ω0 、ω1、 ... ）でPの値を計算するには、 n / 2点（ _ω0 、ω2、 ... ）でAとBの値を再帰的に計算します。 P （ωi）の値は回復するのが非常に簡単です：

P （ωi）= A （ω2 _i ）+ωi⋅B（ω2 _i ）

次数n / 2の多項式の値を考慮する点をξi =ω2 _iで表すと、式は変換されます。

P （ωi）= A （ξi）+ωi⋅B（ξi）

iが0からn - 1までの値を取り、ξi _が 0からn / 2-1までしか定義されていないことを忘れることなく、プログラムに既に駆動できます。 結論-n / 2を法とするiを取る必要があります。

動作時間は、回帰式T （ n ）= O （ n ）+ 2 T （ n / 2 ）で表されます。 これはかなりよく知られた関係であり、 O （n⋅log ₂ n ）で明らかになります（大まかに言うと、再帰の深さはlog ₂ nレベルであり、各レベルですべての呼び出しで合計O （ n ）操作が実行されます）。

何かを書く

非効率的な再帰的FFT実装の例を次に示します。

遅いfft

#include <vector> #include <complex> using namespace std; typedef complex<double> cd; // STL-  .   double,     sin  cos typedef vector<cd> vcd; vcd fft(const vcd &as) { //       1 int n = as.size(); // -    ? if (n == 1) return vcd(1, as[0]); vcd w(n); //   for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; w[i] = cd(cos(alpha), sin(alpha)); } //   A  B vcd A(n / 2), B(n / 2); for (int i = 0; i < n / 2; i++) { A[i] = as[i * 2]; B[i] = as[i * 2 + 1]; } vcd Av = fft(A); vcd Bv = fft(B); vcd res(n); for (int i = 0; i < n; i++) res[i] = Av[i % (n / 2)] + w[i] * Bv[i % (n / 2)]; return res; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

I / Oを追加して、実装が正しいことを確認できます。 多項式P （ x ）= 4 + 3 x + 2 x ² + x ³ + 0⋅x ⁴ + 0⋅x ⁵ + 0⋅x ⁶ + 0⋅x ^7の場合^、値は次のようになります。

P （ w ₀ ）=（ 1 0. 0 0 0、0 . 0 0 0 ）

P （ w ₁ ）=（ 5. 4 1 4、4 . 8 2 8 ）

P （ w ₂ ）=（ 2. 0 0 0、2 . 0 0 0 ）

P （ w ₃ ）=（ 2. 5 8 6、0. 8 2 8 ）

P （ w ₄ ）=（ 2. 0 0 0、0 . 0 0 0 ）

P （ w ₅ ）=（ 2. 5 8 6 、 -0. 8 2 8 ）

P （ w ₆ ）=（ 2. 0 0 0 、 -2. 0 0 0 ）

P （ w ₇ ）=（ 5. 4 1 4 、 -4 . 8 2 8 ）

その場合、大規模なテストで再帰的で素朴な方法を使用できます。

次数2 ^12の多項式では^、この実装は62ミリ秒で動作し、素朴な多項式は1800ミリ秒で動作します。 違いは明らかです。

再帰を取り除く

手順を非再帰的にするには、それについて考える必要があります。 私にとって最も簡単な方法は、MergeSort（マージソート）との類似性を描き、すべての再帰呼び出しを示す図を描くことです。



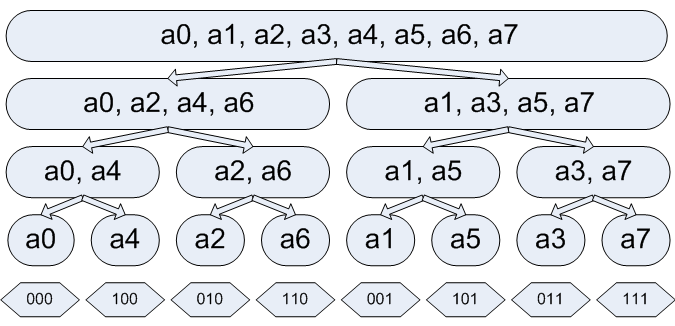
ご覧のとおり、1つの配列を作成し、最初に値fft（ a ₀ ）、fft（ a ₄ ）、fft（ a ₂ ）、 ...で埋めることができます。 数字a _iは、バイナリ表現で「拡張」された数字「 0、1、2、3 、 ... 」であることを理解するのは簡単です。 たとえば、 1 ₁ 0 = 0 0 1 2、4 ₁ 0 = 1 0 0 ₂または6 = 1 1 0 _2、3 = 0 1 1 ₂ 。 これは次のように理解できます。再帰の下位レベルに下降するとき、もう1つの下位ビットを（最後から）決定します。 「通常の」番号付けでは、ビットは最初から決定されます。 したがって、数値を「拡張」する必要があります。 これは、 O （ n forelog ₂ n ）の「額」で行うことも、次のアルゴリズムを使用してO （ n ）に対して動的にプログラムすることもできます。

1. 0からn - 1のサイクルを実行します
2. 数値の最上位ユニットビットの数を格納し、動的に再カウントします。 現在の数が2の累乗である場合にのみ変更されます。1ずつ増加します。
3. 数値の最上位ビットがわかっている場合、整数を反転することは難しくありません。最上位ビット（XOR）を「切り捨て」、残り（既に計算された値）を反転し、「切り捨て」単位を追加します

ここで、「ステップ」からより高いステップを取得できるアルゴリズムを考え出します。 前の手順のすべての値を1つの配列に保存します。 図から明らかなように、最初にk = 1であるkのブロックでデータを処理する必要があり、その後、各ステップで2倍になります。 長さkの 2つのブロックを処理し、出力で長さ2 kの 1つのブロックを取得します。 これがどのように再帰的に行われたかの例を見て、記事の最初から式を思い出して繰り返してみましょう。



2つのブロックをマージするためのプロシージャの引数は、2つのベクトル（もちろん、参照、ソース、結果）、最初のブロックの開始要素の数（2番目のブロックの直後）、ブロックの長さです。 もちろん、イテレータでも実行できます-より多くのSTL'nostiについては、簡潔にするためにこの手順をメインの手順内に転送します。

ブロックマージ

 void fft_merge(const vcd &src, vcd &dest, int start, int len) { int p1 = start; //     int en1 = start + len; //    int p2 = start + len; //     int en2 = star + len * 2; //    int pdest = start; //      int nlen = len * 2; //    for (int i = 0; i < nlen; i++) { double alpha = 2 * M_PI * i / nlen; cd w = cd(cos(alpha), sin(alpha)); //   dest[pdest] = src[p1] + w * src[p2]; if (++p1 >= en1) p1 = start; if (++p2 >= en2) p2 = start + len; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、主な変換手順：

 vcd fft(const vcd &as) { int n = as.size(); int k = 0; //  n   while ((1 << k) < n) k++; vi rev(n); rev[0] = 0; int high1 = -1; for (int i = 1; i < n; i++) { if ((i & (i - 1)) == 0) //    .  i  ,  i-1     . high1++; rev[i] = rev[i ^ (1 << high1)]; //   rev[i] |= (1 << (k - high1 - 1)); //    } vcd cur(n); for (int i = 0; i < n; i++) cur[i] = as[rev[i]]; for (int len = 1; len < n; len <<= 1) { vcd ncur(n); for (int i = 0; i < n; i += len * 2) fft_merge(cur, ncur, i, len); cur.swap(ncur); } return cur; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最適化

次数2 ^{1 6の}多項式では^、再帰は640ミリ秒、再帰なし-500で動作します。改善はありますが、プログラムはさらに高速に実行できます。 ωi =-ωi _{+ n / 2}というプロパティを使用します。 そのため、ルートを2回取ることができず、 a i⋅ωj-複素数のサイン、コサイン、乗算は非常に高価な演算です。

fft_merge（）

 for (int i = 0; i < len; i++) { double alpha = 2 * M_PI * i / nlen; cd w = cd(cos(alpha), sin(alpha)); //   cd val = w * src[p2]; dest[pdest] = src[p1] + val; dest[pdest + len] = src[p1] - val; pdest++; if (++p1 >= en1) p1 = start; if (++p2 >= en2) p2 = start + len; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この最適化による遷移は、「バタフライ変換」と呼ばれます。 プログラムは260ミリ秒動作し始めました。 成功を統合するために、 1のすべての根を計算して配列に書き込みましょう。

fft_merge（）

 int rstep = roots.size() / nlen; //      for (int i = 0; i < len; i++) { cd w = roots[i * rstep]; cd val = w * src[p2];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

fft（）

 roots = vcd(n); for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; roots[i] = cd(cos(alpha), sin(alpha)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

現在、速度は78ミリ秒です。 最初の実装と比較して8倍の最適化！

コードの最適化

現在、すべての変換コードは約55行かかります。 100ではありませんが、これは非常に多く、短くすることもできます。 最初に、 fft_mergeの余分な変数と操作の束を取り除きます：

 void fft_merge(const vcd &src, vcd &dest, int start, int len) { int p1 = start; //int en1 = start + len; //  , .   int p2 = start + len; //int en2 = start + len * 2; //  int pdest = start; //int nlen = len * 2; //      //int rstep = roots.size() / nlen; int rstep = roots.size() / (len * 2); for (int i = 0; i < len; i++) { //cd w = roots[i * rstep]; //       //cd val = w * src[p2]; cd val = roots[i * rstep] * src[p2]; dest[pdest] = src[p1] + val; dest[pdest + len] = src[p1] - val; pdest++, p1++, p2++; //if (++p1 >= en1) p1 = start; //         2len,    len,     //if (++p2 >= en2) p2 = start + len; //  } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、ループをfft_mergeからメインプロシージャに移動できます（ p2 = p1 + lenであるため、 p2も削除できます。これにより、わずかな時間の増加が得られました。これは興味深いです。 ：

fft（）

 for (int len = 1; len < n; len <<= 1) { vcd ncur(n); int rstep = roots.size() / (len * 2); for (int pdest = 0; pdest < n;) { int p1 = pdest; for (int i = 0; i < len; i++) { cd val = roots[i * rstep] * cur[p1 + len]; ncur[pdest] = cur[p1] + val; ncur[pdest + len] = cur[p1] - val; pdest++, p1++; } pdest += len; } cur.swap(ncur); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、変換自体はそれほど多くはかかりません-17行です。 他のすべて-根の事前計算と数値の反転。 作業時間と引き換えにコードを保存する準備ができている場合（ O （ n ）ではなくO （n⋅log ₂ n ））、13行の数字の広がりを次の6行に置き換えることができます。

fft（）の開始時

 vcd cur(n); for (int i = 0; i < n; i++) { int ri = 0; for (int i2 = 0; i2 < k; i2++) //       ri = (ri << 1) | !!(i & (1 << i2)); //      cur[i] = as[ri]; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その結果、コードは次のようになります。

 vcd fft(const vcd &as) { int n = as.size(); int k = 0; //  n   while ((1 << k) < n) k++; vector<int> rev(n); rev[0] = 0; int high1 = -1; for (int i = 1; i < n; i++) { if ((i & (i - 1)) == 0) //    .  i  ,  i-1     . high1++; rev[i] = rev[i ^ (1 << high1)]; //   rev[i] |= (1 << (k - high1 - 1)); //    } vcd roots(n); for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; roots[i] = cd(cos(alpha), sin(alpha)); } vcd cur(n); for (int i = 0; i < n; i++) cur[i] = as[rev[i]]; for (int len = 1; len < n; len <<= 1) { vcd ncur(n); int rstep = roots.size() / (len * 2); for (int pdest = 0; pdest < n;) { int p1 = pdest; for (int i = 0; i < len; i++) { cd val = roots[i * rstep] * cur[p1 + len]; ncur[pdest] = cur[p1] + val; ncur[pdest + len] = cur[p1] - val; pdest++, p1++; } pdest += len; } cur.swap(ncur); } return cur; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

逆変換

もちろん、ポイントで多項式の値を取得するのは良いことですが、フーリエ変換はそれをより良くすることができます-さらに、これらの値を使用して多項式自体を構築します！ 多項式の係数に関してフーリエ変換を値の配列に適用し、結果をnで除算し、セグメントを1からn - 1 （ 0からの番号付け）にすると、元の多項式の係数が得られることがわかります。

ここのコードは非常に単純です-すべてがすでに書かれています。 対処できると思います。

証明

係数v _i （元の多項式には係数a _{iがありました} ）を使用して、多項式P （ x ）に逆変換を適用します。

v _i = a ₀ +ωi a ₁ +ω2 _i a ₂ +ω3 _i a + ...

変換の結果を見てみましょう。

b _i = v ₀ +ωi v ₁ +ω2 _i v ₂ +ω3 _i v ₃ + ...

v _jの値を代入します（ωaωb =ωa _{+ b m o d n} ：



1つの注目すべき事実を証明しましょう： x ≠ 0の場合、 _ω0 +ωx +ω2 _x + ... +ω _{（ n - 1 ） x} = 0 。

これは、根の合計がゼロであるという事実と同様に証明されます。合計をφで表し、両側にωxを掛けて、何が起こったかを確認します。

ここで、この事実をb _iの値の計算に適用します。 _{n - i}を含む行を除くすべての行はゼロにリセットされることに注意してください。



このように：



b _i = a _{n -} i⋅（ _ω0 + _ω0 + _ω0 + _ω0 + ... ）



b _i = a _{n -} i⋅n



証明するために必要でした。

申込み

一般的に言えば、私はすでに記事の冒頭でアプリケーションについて少し話しました。 特に、多項式の乗算は次のように実行できます。

多項式の高速乗算

 vcd a, b; //  //   vcd a_vals = fft(a); vcd b_vals = fft(b); vcd c_vals(a_vals.size()); for (int i = 0; i < a_vals.size(); i++) c_vals[i] = a_vals[i] * b_vals[i]; vcd c = fft_rev(c_vals); //  
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このプログラムの実行時間がO （n⋅log ₂ n ）であり、最も時間のかかる操作がフーリエ変換であることは容易にわかります。 また、2つの多項式でより複雑な式を計算する必要がある場合でも、3つの変換しか実行できないことに注意してください。加算と減算も線形時間で機能します。 残念ながら、多項式はある時点で誤って値0をとることがあるため、除算はそれほど単純ではありません。 UPD2：次数nの 2つの多項式の積の次数が2nになることを忘れないでください。そのため、入力するときは、「余分な」ゼロ先行係数を追加する必要があります。

10進数（またはそれ以上）の数値システムを係数-桁の多項式として表す場合、長い数値の乗算も非常に高速に実行できます。

そして最後に、次の投稿で分析するタスク：文字A、T、G、Cから1 0 ⁵のオーダーの同じ長さの2行があります。文字の最大数が一致するように、行の1つの循環シフトを見つける必要があります。 明らかにO （ n ² ）の単純なソリューションですが、FFTを使用したソリューションがあります。

頑張って



UPD：コード全体をpastebin に投稿しました