キー定義
モルフォロジーという用語は、オブジェクトの形状と構造のプロパティの説明を指します。 マシンビジョンのコンテキストでは、この用語は画像内の領域の形状のプロパティの説明を指します。 数学的モルフォロジーの演算は、最初は集合の演算として定義されていましたが、2次元空間での点の集合の処理の問題にも役立つことがすぐに明らかになりました。 数学的形態のセットは、画像内のオブジェクトを表します。 バイナリイメージのすべての背景ピクセルのセットが、完全な説明のオプションの1つであることは容易にわかります。
まず、数学的形態学を使用して、画像のいくつかのプロパティを抽出します。これは、表示と説明に役立ちます。 たとえば、輪郭、コア、凸包。 予備的および最終的な画像処理の段階で使用される形態学的方法も興味深い。 たとえば、形態学的ろ過、濃厚化または薄化。
数学的形態の装置の入力データは、操作のタイプと解決する問題に応じて、処理済みと特殊の2つの画像です。 このような特別な画像は通常、プリミティブまたは構造要素と呼ばれます。 原則として、構造要素は処理された画像よりもはるかに小さくなります。 構造要素は、何らかの形の領域の記述と考えることができます。 フォームはどのようなものでもかまいませんが、主なことは、所定のサイズのバイナリイメージとして表現できることです。 多くの画像処理パッケージでは、最も一般的な構造要素には特別な名前があります。BOX[H、W]-所定のサイズの長方形、DISK [R]-所定のサイズのディスク、RING [R]-所定のサイズのリング。
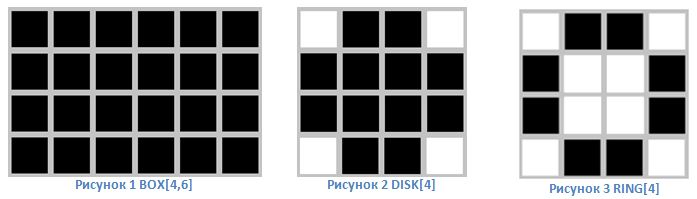
形態学的処理の結果は、元の画像のサイズと構成の両方、および構造プリミティブに依存します。
構造要素のサイズは通常3 * 3、4 * 4または5 * 5ピクセルです。 これは、形態学的処理の主なアイデアによるものであり、その間に画像の特徴的な詳細が検出されます。 望ましい詳細はプリミティブによって記述され、形態学的処理の結果として、画像全体でそのような詳細を強調または削除することができます。
形態学的処理の主な利点の1つは、その単純さです。処理手順の入力と出力の両方で、2値化された画像を取得します。 原則として、他の方法では、最初に元の画像からグレースケールを取得し、次にしきい値関数を使用してバイナリに縮小します。
基本操作
数学的形態学の主な操作は、ビルドアップ、エロージョン、クロージャー、オープニングです。 操作の本質はこれらの名前に反映されています:拡張は画像領域を拡大し、侵食はそれを小さくします、閉鎖操作は領域の内部の穴を閉じて領域の境界に沿った隙間をなくすことを可能にします 次に、形態学的操作の数学的定義を示します。
統一、交差、補数、差異
形態学的操作に進む前に、数学的形態の根底にある集合論的操作を検討することは理にかなっています。
C = A∪Bで示される2つのセットAとBの和集合は、定義上、セットA、セットB、または両方のセットに同時に属するすべての要素のセットです。 同様に、C =A∩Bで示される2つのセットAとBの交点は、定義上、セットAとBの両方に属するすべての要素のセットです。Aの補数は、Aに含まれない要素のセットです。 w∉A}。 2つのセットAとBの差はA \ Bで示され、次のように定義されます:A \ B = {w│w∈A、w∉B} =A∩Bc。 このセットは、Bに含まれていない要素Aで構成されています。
特定の例で上記のすべての操作を検討してください。

乗り換え
ピクセルX のセットからベクトルtへの転送操作X tは、 X t = {x + t |x∈X}の形式で与えられます。 したがって、バイナリイメージで複数の単位ピクセルを転送すると、セットのすべてのピクセルが所定の距離だけシフトされます。 転送ベクトルtは、順序ペア(∆r、∆c)として指定できます。ここで、∆rは行方向の転送ベクトルの成分であり、∆cは画像列の方向の転送ベクトルの成分です。

ビルドアップ、浸食、短絡、破損
特定の例を使用して、次の操作を検討します。 次のバイナリイメージと構造要素があるとします。
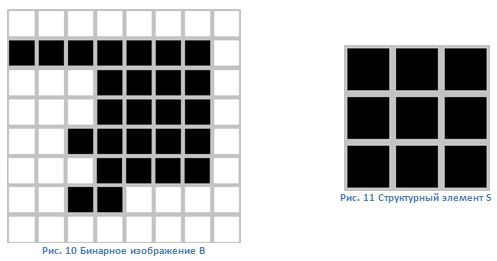
エスカレーション
構造要素Sは、バイナリイメージのすべてのピクセルに適用されます。 毎回、構造要素の原点が単一のバイナリピクセルと結合されると、転送とそれに続くバイナリイメージの対応するピクセルとの論理加算が構造要素全体に適用されます。 論理加算の結果は、最初はゼロ値に初期化されている出力バイナリイメージに書き込まれます。

侵食
侵食操作を実行すると、構造要素も画像のすべてのピクセルを通過します。 ある位置で構造要素の各単一ピクセルがバイナリイメージの単一ピクセルと一致する場合、構造要素の中央ピクセルと出力イメージの対応するピクセルの論理加算が実行されます。

侵食操作の結果として、構造要素より小さいすべてのオブジェクトが消去され、細い線で接続されたオブジェクトが切断され、すべてのオブジェクトのサイズが小さくなります。
オープニング
侵食操作は、小さなオブジェクトやさまざまなノイズを除去するのに役立ちますが、この操作には欠点があります。残りのオブジェクトはすべてサイズが小さくなります。 侵食操作の後、同じ構造要素を持つ拡張操作を使用すると、この影響を回避できます。
開くと、構造要素よりも小さいすべてのオブジェクトが削除されますが、同時にオブジェクトのサイズが大幅に縮小するのを防ぐのに役立ちます。 また、開口部は、太さが構造要素の直径よりも小さい線を削除するのに理想的です。 この操作の後、オブジェクトの輪郭がより滑らかになることを覚えておくことも重要です。

短絡
最初に拡張操作を画像に適用すると、小さな穴や隙間を取り除くことができますが、これによりオブジェクトの輪郭が大きくなります。 この増加を避けると、同じ構造要素で構築した直後に実行される侵食の操作が可能になります。

条件付きビルドアップ
バイナリモフォロジーの典型的なアプリケーションの1つは、形状とサイズが指定された制約を満たすバイナリイメージ内のコンポーネントを分離することです。 このようなタスクの多くでは、バイナリイメージに適用した後、制約を満たさないコンポーネントを削除し、制約を満たすコンポーネントに対応するいくつかの単位ピクセルを残す構造要素を構築できます。 ただし、その後の処理では、侵食後に断片が残るだけでなく、コンポーネント全体が必要になる場合があります。 この問題を解決するために、条件付きエスカレーション操作が導入されました。
侵食の結果として得られた集合は、構造要素Sによって周期的に拡張され、各ステップで結果は元の画像Bの単位値を持つピクセルのサブセットに縮小されます。条件付き拡張操作は次の図で説明されます。 この図では、3ピクセルの高さの垂直フラグメントを含むコンポーネントを選択するために、バイナリイメージBが要素Vによって侵食されています。 結果の画像Cには、このようなコンポーネントが2つあります。 これらのコンポーネント全体を選択するには、元の画像Bに対して要素Cによって画像Cを条件付きで拡大します。

境界線の強調表示
モルフォロジー演算を使用して、バイナリオブジェクトの境界を強調表示することもできます。 この操作は非常に重要です。なぜなら、境界は完全であり、同時にオブジェクトの非常にコンパクトな記述だからです。
境界点の近傍には、少なくとも1つの背景ピクセルがあることが簡単にわかります。 したがって、考えられるすべての隣接要素を含む構造要素に侵食演算子を適用すると、すべての境界点が削除されます...その後、元の画像と侵食の結果として取得された画像のセットの差の操作を使用して境界が取得されます。

このように、数学的形態学の基本操作と、それらの応用のためのいくつかの方法を検討しました。 このデバイスが今後の活動に役立つことを願っています。