Asymmetric Cryptographic Key Distribution Protocols: Denning — Sacco, DASS, Wu Lama

Asymmetric protocols, or protocols based on cryptosystems with public keys, can weaken the requirements for the preliminary stage of protocols. Instead of a shared secret key that two parties must have (either each of the parties and a trusted center), in the protocols considered below, the parties must first exchange public keys (between themselves or with a trusted center). Such a preliminary exchange may take place over an open communication channel, under the assumption that the cryptanalyst cannot influence the contents of the communication channel at this stage.

Denning — Sacco Protocol

The protocol was proposed by Dorothy Denning and Giovanni Sacco in 1981 ( Dorothy E. Denning, Giovanni Maria Sacco ). In this protocol, the initiator (Alice) turns to the trusted center (Trent) for certificates of both participants at once. The same participant is also responsible for the formation of a new session key $$$K$ .

1. $$$Alice \ to \ left \ {A, B \ right \} \ to Trent$
2. $$$Trent \ to \ left \ {S_T (A, K_A, T_T), S_T (B, K_B, T_T) \ right \} \ to Alice$
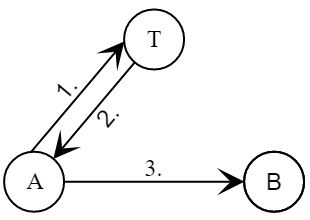
3. Alice generates a new session key $$$K$
   
   $$$\ begin {array} {lll} Alice \ to \ {& E_B (S_A (K, T_A)), & \\ & S_T (A, K_A, T_T), & \\ & S_T (B, K_B, T_T) & \} \ to Bob \ end {array}$
4. Bob verifies the trust center signature on the certificate $$$S_T (A, K_A, T_T)$ decrypts session key $$$K$ and verifies Alice’s signature.

Missing Message $$$E_B (S_A (K, T_A))$ any identifiers makes the protocol vulnerable to attack with a known session key and allows the second side (Bob) to impersonate the initiator (Alice) in a session with a third party (Clara).

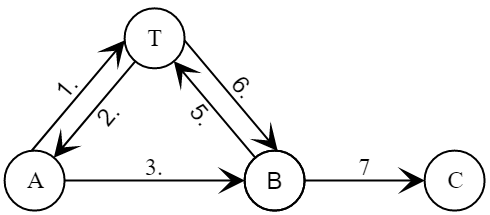
1. Alice and Bob had a protocol session, generating a new session key $$$K$ .
2. $$$Bob \ to \ left \ {B, C \ right \} \ to Trent$
3. $$$Trent \ to \ left \ {S_T (B, K_B, T_T), S_T (C, K_C, T_T) \ right \} \ to Bob$
4. Bob plays messages $$$S_A (K, T_A)$ and $$$S_T (A, K_A, T_T)$ from Alice in a session with Clara:
   
   $$$\ begin {array} {lll} Bob ~ (Alice) \ to \ {& E_C (S_A (K, T_A)), & \\ & S_T (A, K_A, T_T), & \\ & S_T (C, K_C, T_T) & \} \ to Clara \ end {array}$
5. Clara successfully verifies the signature of the trusted center on the certificate $$$S_T (A, K_A, T_T)$ decrypts session key $$$K$ and verifies Alice’s signature.

As a result, Clara is sure that she received a new session key from Alice. $$$K$ .

DASS Protocol

The DASS protocol was an integral part of the Distributed Authentication Security Service (DASS), developed by DEC and described in RFC 1507 in September 1993.



In the DASS protocol, by analogy with the Wide-Mouth Frog and Denning – Sacco protocols, the initiator (Alice) generates a new session key and, for each protocol session, a new pair of sender’s public and private keys. The Trusted Center (Trent) is used as a repository of participants' public key certificates. But unlike Denning-Sacco, both participants turn to the trusted center in turn.

1. $$$Alice \ to \ left \ {B \ right \} \ to Trent$
2. $$$Trent \ to \ left \ {S_T \ left (B, K_B \ right) \ right \} \ to Alice$
3. $$$Alice \ to \ left \ {E_K \ left (T_A \ right), S_A \ left (L, A, K_P \ right), S_ {K_P} \ left (E_B \ left (K \ right) \ right) \ right \} \ to Bob$
4. $$$Bob \ to \ left \ {A \ right \} \ to Trent$
5. $$$Trent \ to \ left \ {S_T \ left (A, K_A \ right) \ right \} \ to Bob$
6. $$$Bob \ to \ left \ {E_K \ left \ {T_B \ right \} \ right \} \ to Alice$

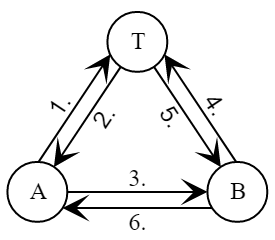
Using public key certificates $$$\ left \ {S_T \ left (B, K_B \ right) \ right \}$ and $$$\ left \ {S_T \ left (A, K_A \ right) \ right \}$ that Trent sends, and further confirmation of ownership of the corresponding keys, participants can authenticate each other. Successfully decrypting timestamps from messages $$$E_K \ left (T_A \ right)$ and $$$E_K \ left \ {T_B \ right \}$ provides proof of ownership of the session key.



The protocol uses the lifetime ( $$$L$ ) session key $$$K_P$ but the timestamp is not included in the message. As a result, the protocol remains vulnerable to an attack with a known session key. Suppose Mellory was able to record a completely past communication session between Alice and Bob, and then was able to access the session key $$$K$ . This allows Mellory to authenticate herself as Alice in front of Bob.

1. $$$Mellory ~ (Alice) \ to \ left \ {E_K \ left (T_M \ right), S_A \ left (L, A, K_P \ right), S_ {K_P} \ left (E_B \ left (K \ right) \ right) \ right \} \ to Bob$
2. $$$Bob \ to \ left \ {A \ right \} \ to Trent$
3. $$$Trent \ to \ left \ {S_T \ left (A, K_A \ right) \ right \} \ to Bob$
4. $$$Bob \ to \ left \ {E_K \ left \ {T_B \ right \} \ right \} \ to Alice$

On the first pass, Mellory changes only the first message containing a time stamp $$$E_K \ left (T_M \ right)$ . Mellory copies the rest from the recorded communication session. If Bob does not record the keys used, he will not notice the spoofing. The simplest fix for this vulnerability is to include a timestamp in the message. $$$S_A \ left (T_A, L, A, K_P \ right)$ .



Since the session key is in the protocol $$$K$ encrypted by the "master" key Bob $$$K_B$ , then compromising the latter will lead to a compromise of all previously used session keys. That is, the protocol does not provide perfect direct secrecy (goal G9).



Neither Trent nor Bob are involved in the formation of new session keys. Therefore, Alice can force Bob to use the old session key, as in the Wide-Mouth Frog and Yahalom protocols.

Wu Lama Protocol

The Wu-Lama protocol, proposed in 1992 ( Thomas YC Woo, Simon S. Lam ), adds random numbers of participants to messages, which protects the protocol, including from repeated attacks, and also provides confirmation of key ownership. It is also the only protocol considered in this section in which a new key is generated by a trusted party (Trent).

1. $$$Alice \ to \ left \ {A, B \ right \} \ to Trent$
2. $$$Trent \ to \ left \ {S_T (K_B) \ right \} \ to Alice$
3. $$$Alice \ to \ left \ {E_B (A, R_A) \ right \} \ to Bob$
4. $$$Bob \ to \ left \ {A, B, E_T (R_A) \ right \} \ to Trent$
5. $$$Trent \ to \ left \ {S_T (K_A), E_B (S_T (R_A, K, A, B)) \ right \} \ to Bob$
6. $$$Bob \ to \ left \ {E_A (S_T (R_A, K, A, B), R_B) \ right \} \ to Alice$
7. $$$Alice \ to \ left \ {E_K (R_B) \ right \} \ to Bob$

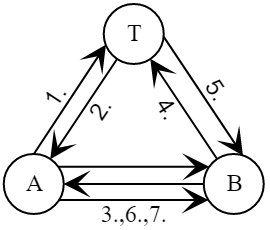
Since in the session key certificate $$$S_T (R_A, K, A, B)$ Alice's random number is present $$$R_A$ , the attacker will not be able to use the old certificate in a new session on behalf of Bob. Therefore, the 6th pass of the protocol allows Alice to make sure that Bob knows the new session key $$$K$ , and therefore owns his "master" key $$$K_B$ (as this is the only way to get the certificate from the message $$$E_B (S_T (R_A, K, A, B)))$ )



Message $$$E_K (R_B)$ from Alice to Bob on the seventh passage allows us to guarantee at the same time that Alice knows her “master” key $$$K_A$ (since it was able to decrypt $$$E_A (\ dots, R_B)$ ), and a new session key $$$K$ because it was able to correctly encrypt $$$R_B$ this key.