Why top physicists do not like a multi-world interpretation

Recently, praises have been heard from each iron about the multivariate interpretation of quantum mechanics and negative towards Copenhagen. Here, for example, a relatively recent article on Habré . Adherents of the ideas of the founding fathers (Niels Bohr, Werner Heisenberg, Paul Dirac, Wolfgang Pauli) are now considered dinosaurs who refuse to accept the modern (1957) multi-world interpretation.

Indeed, at first glance, a multi-world interpretation seems logical and among the uninitiated, acquaintance with it usually causes bewilderment like “How can one argue with this? Still obvious! Why are scientists holding on to Copenhagen? ” But, as always, the devil is in the details. The founding fathers, unlike the alcoholic Hugh Everett, were not fools.

Copenhagen interpretation

Quantum mechanics is a framework, a set of postulates (axioms). Different sources give a different number of them. In some cases, some postulates can be deduced from others. But then the presentation of the already complex material is even more complicated, so usually 5-6 pieces are formulated.

This framework can be applied to various situations and develop more detailed theories based on it: non-relativistic quantum particle mechanics, relativistic quantum mechanics, quantum field theory (electromagnetic, strong, weak, Higgs, etc.), string theory, solid state physics and many more of what.

Most postulates associate abstract mathematical structures with physics, for example:

The observed quantities correspond to Hermitian operators.

or

When measuring the value corresponding to a given operator, it is possible to obtain only one of the eigenvalues ​​of this operator.

or

The state of the system (the maximum possible information about the system) is described by a vector in a Hilbert space called a state vector.

These abstract postulates are not taken from the ceiling, but from the criterion of the correspondence of the predictions of the theory to experimental data. For further discussion, we will need the following two postulates. Measurement postulate:

When measuring the value corresponding to a given operator, the state vector collapses into one of the eigenvectors of the given operator, and one that corresponds to the measured eigenvalue.

and the Bourne rule:

The probability that during measurement we obtain a given eigenvalue of the operator is equal to the square of the absolute value of the scalar product of the current state vector with the corresponding eigenvector of the operator.

Pretty abstract, isn't it?

As I noted, many postulates are interconnected. For example, the fact that a scalar product must be squared, and not in a cube, let’s say, can be deduced from other postulates.

So, we apply this mathematical colossus to the famous "paradox" of the cat Schrödinger.

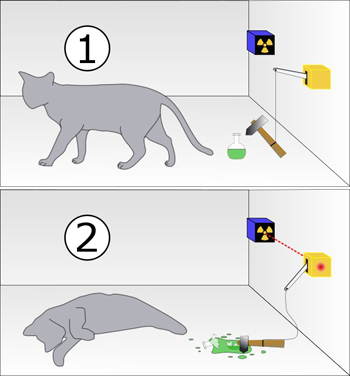
We need to measure the state of the cat (alive / dead). According to the postulate, such a measured quantity must correspond to a Hermitian operator. Indeed, you can find one. Operators that answer yes / no questions (is the cat alive?) Are called projection operators. They have only two eigenvalues ​​- zero and one. A unit in our case corresponds to a living cat, zero to a dead cat.

According to the postulate, when measuring, we can get only one of these two eigenvalues. Therefore, we will never get alive + dead. There is no such eigenvalue corresponding to a vector $$ our projection operator. Everything, the "paradox" has been exhausted.

But quantum mechanics also allows us to calculate the likelihood that upon observation we will have a living cat, and the probability that it is dead. Let's say the state of the cat is described by the vector $$ . The probability that a cat will be alive upon observation, according to the Bourne rule, is:

$$

and the fact that he is dead:

$$

That's all, boring quantum mechanical calculations are over. There are theorems showing that it is impossible to extract more information than these probabilities in principle.

Multiworld interpretation

-

Adherents of a world-wide interpretation simply discard the last two postulates. We do not need them, superfluous.

But it is clear that if they could have been dispensed with, the founding fathers would not have introduced them. What do the supporters of the multiworld replace them with? Oddly enough, in many worlds.

All alternatives are implemented in a particular world. If the system is described by a vector $$ , then the universe is divided into two worlds: in one, the cat is alive, and in the other, dead.

-

Brilliant, isn't it? And attractively purely psychologically. It's nice to think that there are worlds where you are a billionaire.

But the multiworld comes to a standstill if you just take other coefficients (probability amplitudes) before the vectors $$ and $$ . Take for example:

$$

The standard Copenhagen interpretation says that when observed with a 99% probability, we will see a dead cat. And believe me, it will be so. But what has changed in the world? Nothing. As there were two worlds, it remains. The probability should be 0.5.

Particularly advanced adherents say that "branch thickness" has changed. But please explain to me what this thickness depends on and what makes it change? How does the word "branch thickness" differ from the word "probability"? Still, you need a Bourne rule, is it just that probability is replaced by thickness? Well, OK.

Actually, in the original version of the experiment, the fate of the cat is associated with whether the atom decayed or not. The probability that an atom decays increases over time, while the fact that it does not decay decreases. In the framework of the standard Copenhagen interpretation, one can even find the exact dependence of probability on time.

Many-worldly adepts apparently turn out that the “branch thickness” changes with time. In general, 1% but the real world and 99% but the real world somehow do not look very beautiful.

Another group claims that one hundred worlds will form.

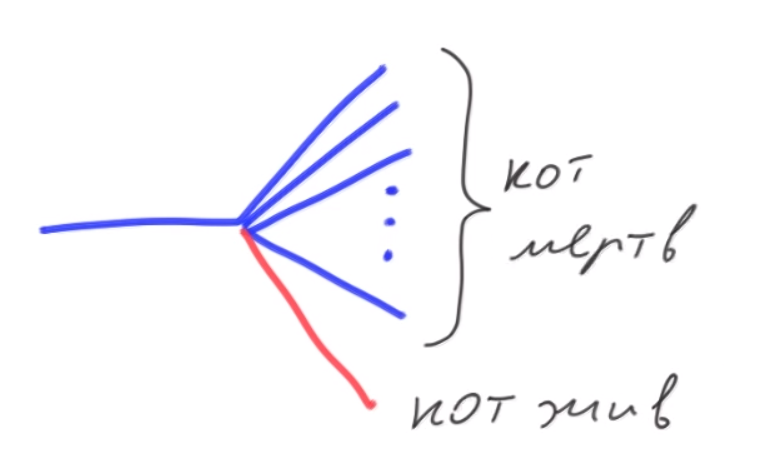
In one, the cat is alive, and in 99 dead. But where did a hundred come from, if there are only two terms in a superposition: alive + dead? It is argued, after all, that a multivariate interpretation does not change the mathematics of CM. And again, the probabilities change over time. Over time, more and more worlds with a dead cat appear? Even if I ended up in a world with a live cat?

Speaking of time. In the Heisenberg representation, the state vector is generally static, and with time the operators change. But a multi-world interpretation works only in Schrödinger's view, when time evolution is assigned to the state vector (wave function). It turns out all the same, it is not compatible with all the mathematics of standard KM, as stated.

When exactly do these branches occur? Will observers from different reference frames agree on the branching time? Has anyone even tried to combine the multiworld with the theory of relativity?

Another argument is connected with such a nuance of quantum mechanics that the observer can choose a basis in which the observed quantity will be measured. With a Schrödinger cat, it’s not entirely obvious which other basis can be used. But if we consider something “more quantum,” the electron spin, for example, then despite the fact that during measurement we also get only one of two values ​​(spin up or spin down), the form of the Hermitian operator for spin will be different for different bases. And there are infinitely many of them. It is associated with the choice of the axis relative to which the spin will be measured.

But there are infinitely many directions in space. The probability distribution of what the spin will turn out in the measurement depends on the chosen direction (basis).

We attach a device for measuring the back to an automaton that kills a cat. Then it turns out that his fate is connected with the result of measuring the spin and the observer's choice of a certain basis. It turns out that the experimenter determines by his choice how many worlds the universe will share?

How many worlds are formed? Two for each of the spin measurements (up / down) and infinity for each of the bases? Two times infinity?

And if you measure some quantity, the operator of which has a continuous spectrum. For example, to which of the infinite number of points on the screen does the photon get after passing a double-slit plate.

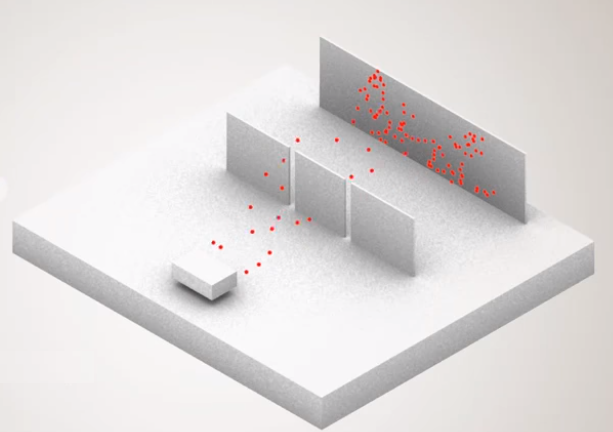
And if the observer again wants to change the basis. It will not measure the coordinate, but the momentum. How many worlds will appear? Infinity multiplied by two?

And if you measure a quantity with a continuous spectrum and choose a basis, you can from the infinity of possibilities. How many worlds will be formed? Infinity multiply by infinity?

OK, I know that George Cantor came up with cardinal and ordinal numbers for such cases. Idea for scientific freaks: try to describe a multi-world interpretation with their use. No wonder these different infinities exist in the Platonic world of ideas. At least they’ll do for something.

Many other arguments can be given. Why and how these worlds can unite again, and they should be able to unite, because before evolution quantum evolution is reversible. And since the postulates of measurement have been removed in a multi-world interpretation, evolution is always reversible. How are quantum entanglement experiments explained? And so on and so forth…

In general, with these crazy ideas, Hugh Everett went to Niels Bohr himself, who laughed at him.

Haha

What is collapse?

Proponents of the multi-worlds hope that the Bourne rule will someday be derived from the "physics of world division." Probabilities are not fundamental, they say. I will disappoint you, but this will never happen. It is impossible to construct a probabilistic theory without introducing probability initially.

Particularly vehemently adherents criticize the postulate of measurement. What does he mean?

During measurement, the state vector (wave function) collapses into one of the eigenvectors of the operator of the measured quantity. In the case of the Schrödinger cat, these are vectors $$ and $$ . The postulate simply says: whatever the state vector before measurement, if you saw a live cat, now the system should be described by a vector $$ . If you saw a dead cat, then you must now describe it with a vector $$ .

That is, the collapse reflects the updating of the observer's knowledge when he receives new information. This is a subjective process. No physical process is associated with collapse. And yes, different observers can describe the same system with different state vectors. And collapse for them can occur at different times. This can be seen in the example of a mental experiment with a Wigner friend .

You can draw an analogy with a coin toss.

Initially, you describe the system with probabilities: 50%, that the eagle will fall, and 50%, that the tails. But after the tossing, either an eagle or a tails falls out. You update your information and describe the current state of the system as 100% heads and 0% heads. There was a “collapse” of the probability distribution into one of the realized alternatives.

Quantum mechanics in its standard Copenhagen interpretation is subjective. Neither an observer nor observation (measurement) can be thrown out of it.

Feynman on a multi-world interpretation

Richard Feynman is commonly cited as an example of a quantum physics guru. He devoted a multivariate interpretation of as much as 30 seconds from his life. This moment was saved as a transcript of the conference . Feynman expressed the view that a multi-world interpretation is complete nonsense and never returned to it again.