Algorithm for calculating the root of the nth degree from an arbitrary positive number

I came across an interesting puzzle: Indeed, the number a and the positive integer n are given. Calculate the nth root of a number without using libraries.



Input data: the number a is real, non-negative, does not exceed 1000, is specified with an accuracy of 6 decimal places. The number n is natural, does not exceed 10.

Output: The program should output a single number: the answer to the problem with an accuracy of at least 5 decimal places.



Naturally, it was interesting to solve it in a draft with a pencil, and then draw it in the editor and try to compile. Without googling, hints and even more so the use of libraries. If you are solving this for the first time, then first try writing a program to find the usual square root. If the task seems to you difficult, solve almost the same, but simpler. Then your fear will go away and some kind of rough understanding will arise.



So for starters, I’ll give an example of how to calculate the square root without using a library function. Sequential Iteration Algorithm. It converges quite quickly even for large numbers.

/* Calculating the square root by iterations */ #include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

You can run the code here: CLICK



Logarithmic complexity of the algorithm? Or another? :)



Now you can move on to the complicated version of the task. In this case, the solution is more generalized.

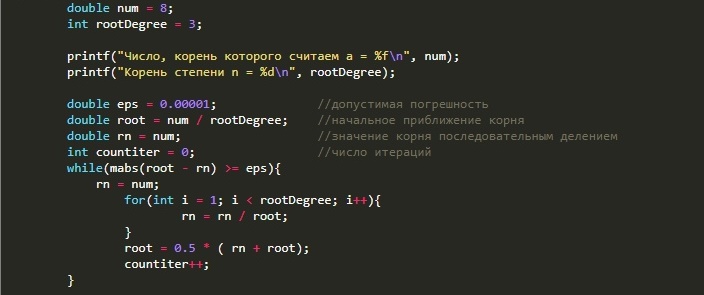
 #include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(",     = %f\n", num); printf("  n = %d\n", rootDegree); double eps = 0.00001; //  double root = num / rootDegree; //   double rn = num; //    int countiter = 0; //  while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf("  = %i\n", countiter); return 0; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

You can run the code here: CLICK



In this solution, I use the idea of ​​a relatively good initial approximation. Then sequential division is the second approximation of the root of the nth degree. Next, a new approximation is considered by averaging the two current ones. Consistently, the algorithm converges to the desired root with a predetermined error. This is a bit like a simple iteration method.



This is the first working algorithm written on the knee. We still need to reflect on the complexity and possibilities of acceleration. By the way, what features of acceleration of this algorithm can be implemented in your opinion?



I feel that there will be a question: “Why do this if everything was implemented in libraries a hundred years ago ?!”



Answer: Personally, I always liked to think about algorithms that are already implemented in standard libraries. Try to develop them yourself (well, or to develop some kind of slowly working parody and fail). It trains the brain very well. Therefore, in my opinion, “reinventing the wheel” is very useful. And it is categorically harmful to always use everything ready, without any idea of ​​the internal structure.