Share, fish, quickly and completely

Division is one of the most expensive operations in modern processors. There is no need to go far for proof: Agner Fog [ 1 ] broadcasts that on Intel / AMD processors we can easily get Latency in 25-119 clock cycles, and reciprocal throughput - 25-120. Translated into Russian - SLOW ! Nevertheless, there is an opportunity to avoid the division instruction in your code. And in this article, I’ll tell you how it works, in particular in modern compilers (they have been able to do this for 20 years already), and I’ll also tell how the knowledge gained can be used to make the code better, faster, more powerful.



Actually, I’m talking about: if the divisor is known at the compilation stage, it is possible to replace integer division with multiplication and a logical shift to the right (and sometimes you can do without it at all - I'm certainly talking about the implementation in the Programming Language). It sounds very encouraging: the operation of integer multiplication and a shift to the right by, for example, Intel Haswell will take no more than 5 clock cycles. It remains only to understand how, for example, by performing integer division by 10, to obtain the same result by integer multiplication and a logical shift to the right? The answer to this question lies through understanding ... Fixed Point Arithmetic (hereinafter FPA). A little bit of basics.



When using FP, the exponent (exponent 2 => the position of the point in the binary representation of the number) is not saved in the number (unlike floating point arithmetic, see IEE754), but it is considered to be some agreed upon quantity known to programmers. They only save the mantissa (what comes after the decimal point). Example:

$$

$$0.1 = .0001 1001 1001 1001 (1001) ... FP, exp = 0$$

0.1 - in binary notation it has 'infinite representation', which is indicated by parentheses in the example above - this part will be repeated from time to time, following each other in binary FP notation of number 0.1.



In the example above, if we use 16-bit registers for storing FP numbers, we cannot fit the FP representation of 0.1 into such a register without losing accuracy, and this in turn will affect the result of all further calculations in which the value of this register is involved.



Suppose we are given a 16-bit integer A and a 16-bit Fraction part of B. The product of A by B results in a number with 16 bits in the integer part and 16 bits in the fractional part. To get only the integer part, obviously, you need to shift the result by 16 bits to the right.



Congratulations, the introduction to the FPA is over.



We form the following hypothesis: to perform an integer division by 10, we need to multiply the Divisible Number by the FP representation of the number 0.1, take the integer part and the matter in the hat ... wait a minute ... But will the result be accurate, more precisely, the integer part? - After all, as we recall, only an approximate version of the number 0.1 is stored in our memory. Below I wrote three different representations of the number 0.1: an infinitely accurate representation of the number 0.1, a representation of the number 0.1 truncated after the 16th bit without rounding, and a representation of the number 0.1 cut off after the 16th bit with a rounding.

$$

$$0001 \: 1001 \: 1001 \: 1001 \: | \: 1001 \: 1001 .... - infinity \: precision \: \: \: \: \: \: \: \: \: \: \ : \: \: \: \: \: \: \: \: \: \: \: \\ 0001 \: 1001 \: 1001 \: 1001 \: | \: 0000 \: 0000 .... - truncating \: without \: rounding \\ 0001 \: 1001 \: 1001 \: 1010 \: | \: 0000 \: 0000 .... - truncating \: with \: rounding \: up \:$$

Let us estimate the errors of truncating representations of the number 0.1:

$$

$$infinity \: precision - truncating \: without \: rounding = 0.6 * 2 ^ {- 16} \\ truncating \: with \: rounding \: up - infinity \: precision = 0.1 * 2 ^ {- 14}$$

In order for the result of multiplying the integer A by the Approximation of 0.1 to give the exact integer part, we need to:

$$

$$IntegerPart (A * 0.1) = IntegerPart (A * (0.1 + 0.1 * 2 ^ {- 14})),$$

either

$$

$$IntegerPart (A * 0.1) = IntegerPart (A * (0.1 + 0.6 * 2 ^ {- 16}))$$

It is more convenient to use the first expression: when $$$0.1 * 2 ^ {-14} * A <0.1$ we always get the identity (but, mind you, not all decisions are more than enough within the framework of this problem). Solving, we get $$$A <2 ^ {14}$ . That is, multiplying any 14-bit number A by truncating with rounding up the representation of 0.1, we always get the exact integer part, which we would get by multiplying infinitely exactly 0.1 by A. But, by convention, we are multiplying 16-bit numbers, which means , in our case the answer will be inaccurate and we cannot trust in simple multiplication by truncating with rounding up 0.1. Now, if we could save in the FP representation of the number 0.1 not 16 bits, but, say, 19, 20, then everything would be OK. And after all we can!

We carefully look at the binary representation - truncating with rounding up 0.1: the highest three bits are zero, which means that they do not make any contribution to the multiplication result (new bits).

Therefore, we can shift our number to the left by three bits, round up and, after doing the multiplication and logical shift to the right, first by 16, and then by 3 (that is, generally speaking at a time by 19) - we get the desired, exact integer part . The proof of the correctness of such a '19' bit multiplication is similar to the previous one, with the only difference being that it works correctly for 16-bit numbers. Similar reasoning is also true for numbers of greater capacity, and not only for division by 10.



Earlier, I wrote that, generally speaking, you can do without any shift at all, limiting yourself to multiplication. How? Assembler x86 / x64 on the drum:

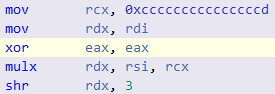
In modern processors, there is a MUL command (there are also analogues of IMUL, MULX - BMI2), which, taking one, say 32/64-bit parameter, is capable of performing 64/128 bit multiplication, saving the result in parts in two registers (high 32/64 bits and younger, respectively):

MUL RCX ;  RCX  RAX,   (128 )   RDX:RAX
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Let some integer 62-bit A be stored in the RCX register, and let the 64-bit FA representation truncating with rounding up of the number 0.1 be stored in the RAX register (notice, there are no left shifts). After completing 64-bit multiplication, we get that the highest 64 bits of the result are stored in the RDX register, or, more precisely, the integer part, which will be exact for 62 bit numbers. That is, a shift to the right (SHR, SHRX) is not needed. The presence of such a shift loads the processor’s Pipeline, regardless of whether it supports OOOE or not: at least there is an extra dependency in the most likely already long chain of such dependencies (aka Dependency Chain). And here, it is very important to mention that modern compilers, seeing an expression of the form some_integer / 10, automatically generate assembler code for the entire range of Divisible numbers. That is, if you know that your numbers are always 53-bit (this is exactly what happened in my task), then you will get an extra shift instruction anyway. But, now that you understand how this works, you can easily replace division yourself with multiplication, without relying on the mercy of the compiler. By the way, getting the high bits of a 64-bit product in C ++ code is implemented by something like mulh, which, according to Asm code, should be equivalent to the lines of the {I} MUL {X} instruction above.



Perhaps with the advent of contracts (in C ++ 20 we are not waiting) the situation will improve, and in some cases, we can trust the car! Although this is C ++, the programmer is responsible for everything here - not otherwise.



The reasoning described above - applies to any divisors of constants, well, and below is a list of useful links:



[1] https://www.agner.org/optimize/instruction_tables.pdf

[2] Steeper than Agner Fogh

[3] Telegram channel with useful information about optimizations for Intel / AMD / ARM

[4] About division entirely, but in English