Smart String Processing Algorithms in ClickHouse

ClickHouse constantly encounters string processing tasks. For example, searching, calculating the properties of UTF-8 strings, or something more exotic, whether it is a case-sensitive search or a compressed data search.

It all started with the fact that ClickHouse development manager Lyosha Milovidov o6CuFl2Q came to us at the Faculty of Computer Science at the Higher School of Economics and offered a huge number of topics for term papers and diplomas. When I saw “Smart String Processing Algorithms in ClickHouse” (I, a person who is interested in various algorithms, including experimental ones), I immediately set up plans for how to make the coolest diploma. My joy and expression can be described as follows:

Clickhouse

ClickHouse carefully thought out the organization of data storage in memory - in columns. At the end of each column there is a padding of 15 bytes for safe reading of a 16-byte register. For example, ColumnString stores null terminated strings along with offsets. It is very convenient to work with such arrays.

There are also ColumnFixedString, ColumnConst and LowCardinality, but we will not talk about them in more detail today. The main point at this point is that the design for safe reading of tails is just fine, and data locality also plays a role in processing.

Substring Search

Most likely, you know many different algorithms for finding a substring in a string. We will talk about those that are used in ClickHouse. First we introduce a couple of definitions:

1. haystack - the line in which we are looking; typically length is denoted by n .
2. needle - the string or regular expression that we are looking for; the length will be denoted by m .

After studying a large number of algorithms, I can say that there are 2 (maximum 3) types of substring search algorithms. The first is the creation in one form or another of suffix structures. The second type is algorithms based on memory comparison. There is also the Rabin-Karp algorithm, which uses hashes, but it is quite unique in its kind. The fastest algorithm does not exist, it all depends on the size of the alphabet, the length of the needle, haystack and frequency of occurrence.

Read about different algorithms here . And here are the most popular algorithms:

1. Knut - Morris - Pratt,
2. Boyer - Moore,
3. Boyer - Moore - Horspool,
4. Rabin - Carp,
5. Double-sided (used in glibc called “memmem”),
6. BNDM

The list goes on. We at ClickHouse honestly tried everything, but in the end we settled on a more extraordinary version.

Volnitsky Algorithm

The algorithm was published on the blog of programmer Leonid Volnitsky at the end of 2010. It somewhat resembles the Boyer-Moore-Horspool algorithm, only an improved version.

If m <4 , then the standard search algorithm is used. Save all the bigrams (2 consecutive bytes) needle from the end into a hash table with open addressing of size | Sigma | ² elements (in practice, these are 2 ¹⁶ elements), where the offsets of this bigram will be the values, and the bigram itself will be the hash and index at the same time. The initial position will be at position m - 2 from the beginning of the haystack. We follow haystack with a step of m - 1 , look at the next bigram from this position in haystack and consider all the values ​​from the bigram in the hash table. Then we will compare two pieces of memory with the usual comparison algorithm. The tail that remains will be processed by the same algorithm.

Step m - 1 is chosen in such a way that if there is an occurrence of needle in a haystack, then we will definitely consider the bigram of this entry - thereby ensuring that we return the position of the entry in haystack. The first occurrence is guaranteed by the fact that we add indexes from the end to the hash table by bigram. This means that when we go from left to right, we will first consider the bigrams from the end of the line (perhaps initially considering completely unnecessary bigrams), then closer to the beginning.

Consider an example. Let the string haystack be abacabaac



and needle equal to aaca



. The hash table will be {aa : 0, ac : 1, ca : 2}



.

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -   
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

We see the bigram ac



. In needle it is, we substitute in the equality:

 0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

It did not match. After ac



there are no entries in the hash table, we step with step 3:

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -   
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

There are no bigrams ba



in the hash table, go ahead:

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -   
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

There is a bigram ca



in needle, we look at the offset and find the entry:

 0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The algorithm has many advantages. Firstly, you can not allocate memory on the heap, and 64 KB on the stack is not something transcendental now. Secondly, 2 ¹⁶ is an excellent number to take modulo for the processor; these are just movzwl instructions (or, as we joke, “movsvl”) and the family.

On average, this algorithm proved to be the best. We took the data from Yandex.Metrica, the requests are almost real. One stream speed, more is better, KMP: Knut - Morris - Pratt algorithm, BM: Boyer - Moore, BMH: Boyer - Moore - Horspool.

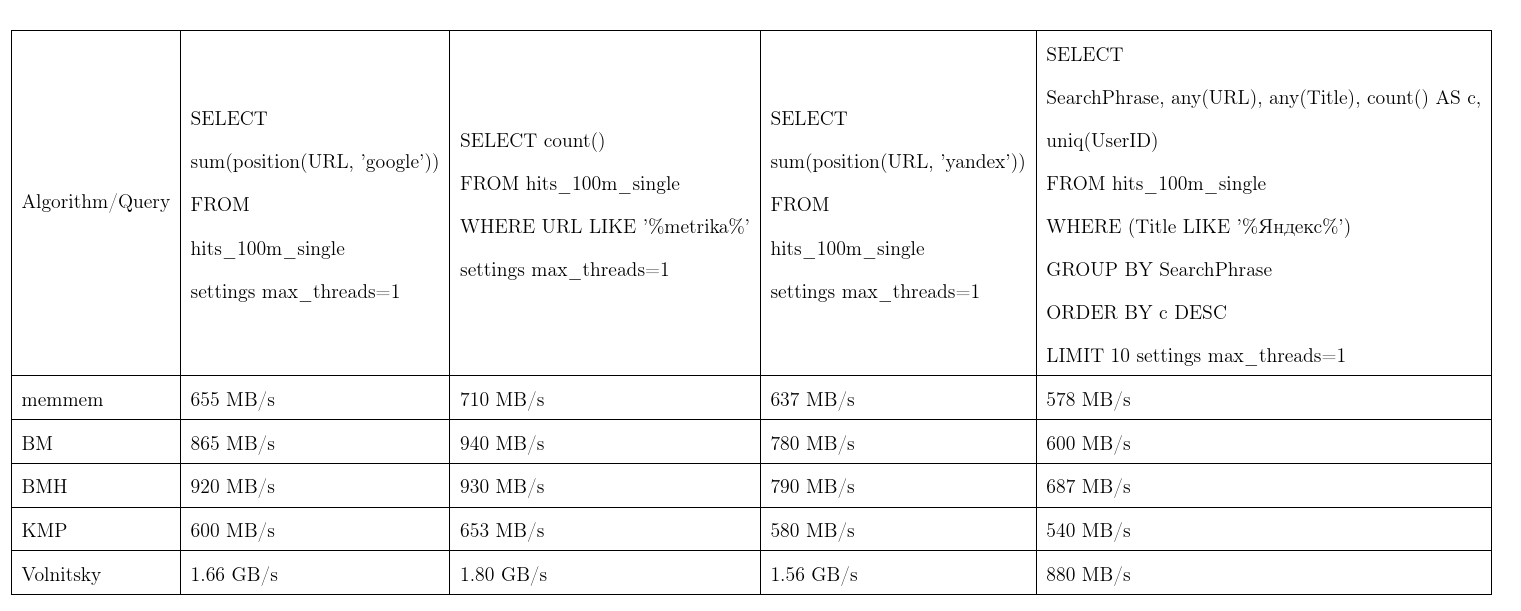
In order not to be unfounded, the algorithm can work quadratic time:

It is used in the position(Column, ConstNeedle)



function position(Column, ConstNeedle)



, and also acts as an optimization for regular expression searches.

Regular Expression Search

We’ll tell you how ClickHouse optimizes regular expression searches. Many regular expressions contain inside a substring, which must be inside a haystack. In order not to build a finite state machine and check on it, we will isolate such substrings.

To do this is quite simple: any opening brackets increase the level of nesting, any closing brackets decrease; there are also characters specific to regular expressions (e.g. '.', '*', '?', '\ w', etc.). We need to get all the substrings at level 0. Consider an example:

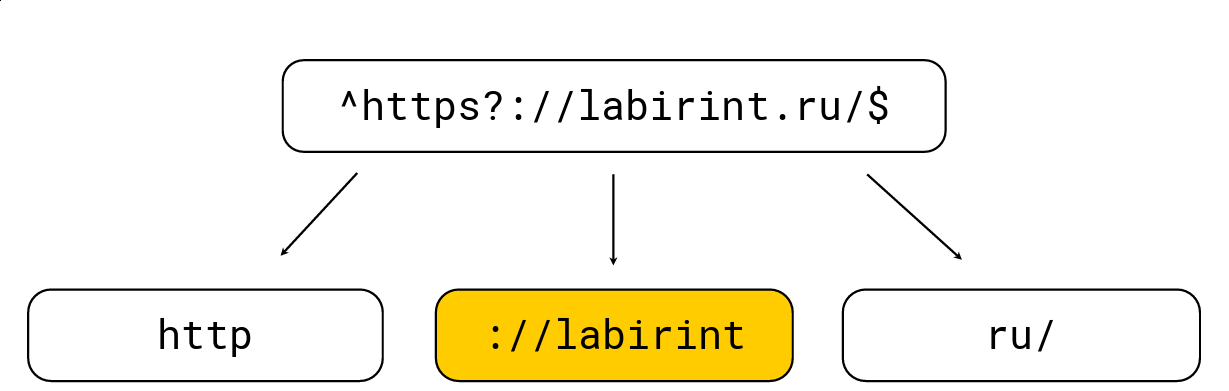
We break it into those substrings that must be in the haystack from the regular expression, after which we select the maximum length, look for candidates on it and then check with the usual regular expression engine RE2. There is a regular expression in the picture above, it is processed by the usual RE2 engine at 736 MB / s, Hyperscan (about it a bit later) manages to 1.6 GB / s, and we manage 1.69 GB / s per core along with decompression LZ4. In general, such optimization is on the surface and greatly accelerates the search for regular expressions, but often it is not implemented in tools, which greatly surprises me.

The LIKE keyword is also optimized using this algorithm, only after LIKE can a very simplified regular expression come in %%%%%% (arbitrary substring) and _



(arbitrary character).

Unfortunately, not all regular expressions are subject to such optimizations, for example, from yandex|google



it is impossible to explicitly isolate substrings that must occur in haystack. Therefore, we came up with a completely different solution.

Search for many substrings

The problem is that there is a lot of needle, and I want to understand if at least one of them is included in the haystack. There are quite classical methods for such a search, for example, the Aho-Korasik algorithm. But he was not too fast for our task. We’ll talk about this a bit later.

Lesha ClickHouse loves non-standard solutions, so we decided to try something else and, perhaps, make a new search algorithm ourselves. And they did.

We looked at the Volnitsky algorithm and modified it so that it began to search for many substrings at once. To do this, you just need to add the bigrams of all the rows and store the row index in the hash table. The step will be selected from at least all needle lengths minus 1 to again guarantee the property that if there is an occurrence, we will see its bigram. The hash table will grow to 128 KB (lines longer than 255 are processed by the standard algorithm, we will consider no more than 256 needles). I am very lazy, so here is an example from the presentation (read from left to right from top to bottom):

We began to look at how such an algorithm behaves in comparison with others (rows are taken from real data). And for a small number of lines, he does everything (the speed along with unloading is indicated - about 2.5 GB / s).

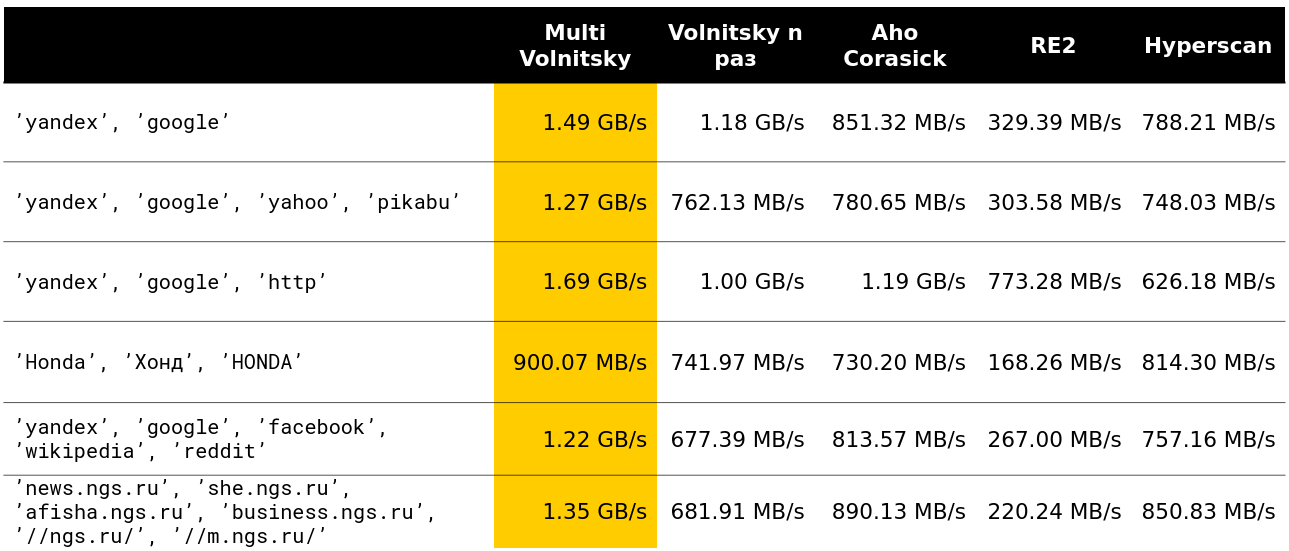
Then it became interesting. For example, with a large number of similar bigrams, we lose to some competitors. It is understandable - we begin to compare many pieces of memory and degrade.

You can not accelerate much if the minimum length of the needle is large enough. Obviously, we have more opportunities to skip whole pieces of haystack without paying anything for it.

The tipping point begins somewhere on lines 13-15. About 97% of the requests I saw on the cluster were less than 15 rows:

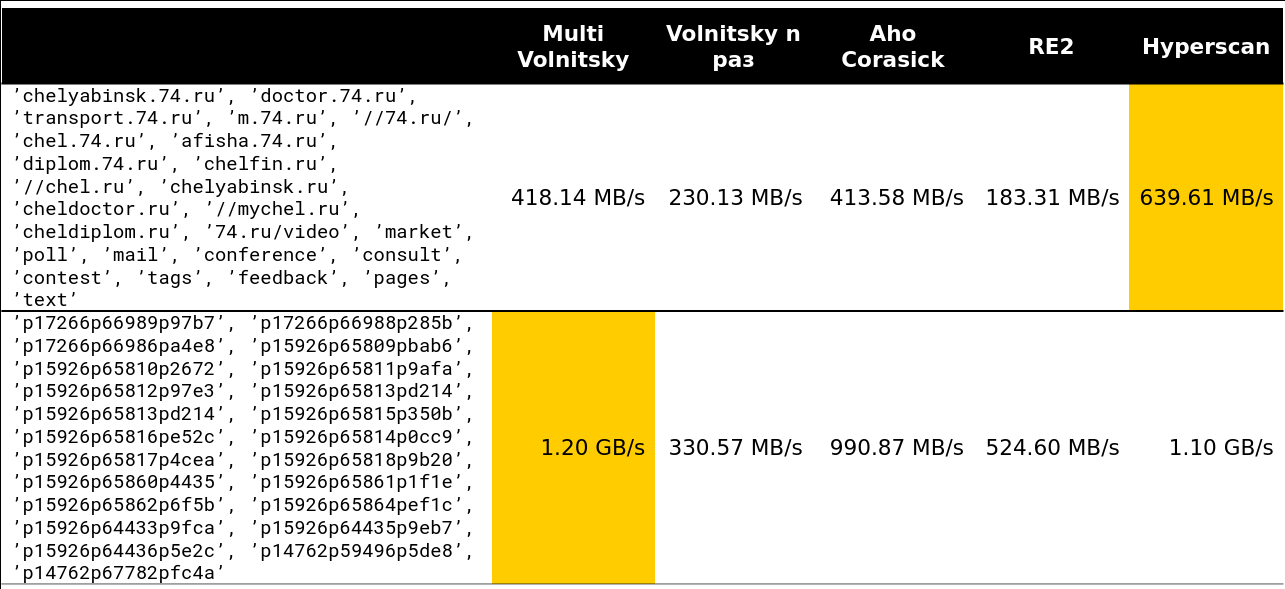
Well, a very scary picture - 41 lines, many repeating bigrams:

As a result, in ClickHouse (19.5) we implemented the following functions through this algorithm:

- multiSearchAny(h, [n_1, ..., n_k])



- 1, if at least one of the needles is in the haystack.

- multiSearchFirstPosition(h, [n_1, ..., n_k])



- the leftmost position to enter the haystack (from one) or 0 if not found.

- multiSearchFirstIndex(h, [n_1, ..., n_k])



- the leftmost needle index, which was found in haystack; 0 if not found.

- multiSearchAllPositions(h, [n_1, ..., n_k])



- all the first positions of all needles, returns an array.

The suffixes are -UTF8 (we do not normalize), -CaseInsensitive (add 4 bigrams with different case), -CaseInsensitiveUTF8 (there is a condition that uppercase and lowercase letters must be the same number of bytes). See the implementation here .

After that, we wondered if we could do something similar with many regular expressions. And they found a solution that was already spoiled in benchmarks.

Search for many regular expressions

Hyperscan is a library from Intel that searches immediately for many regular expressions. It uses heuristics to isolate subwords from regular expressions that we wrote about, and a lot of SIMDs to search for the Glushkov automaton (the algorithm seems to be called Teddy).

In general, everything is in the best traditions of getting the maximum out of the search for regular expressions. The library really does what is declared in its functions.

Fortunately, in my ClickHouse development month, I was able to overtake 12-year development in a decent class of queries and I am very pleased with that.

In Yandex, the Hyperscan library is also used in antispam. Judging by the reviews, she calmly processes thousands of regular expressions and quickly searches for them.

The library has several disadvantages. The first is the undocumented amount of memory consumed and a strange feature that haystack must be less than 2 ³² bytes. The second - you can’t return the first positions for free, the leftmost needle indices, etc. And the third minus - there are some bugs out of the blue. Therefore, at ClickHouse, we implemented the following functions using Hyperscan:

- multiMatchAny(h, [n_1, ..., n_k])



- 1, if at least one of the needles came up with haystack.

- multiMatchAnyIndex(h, [n_1, ..., n_k])



- any index from needle that multiMatchAnyIndex(h, [n_1, ..., n_k])



haystack.

We are interested, but how can you search not exactly, but approximately? And came up with several solutions.

Approximate search

The standard in approximate search is the Levenshtein distance - the minimum number of characters that can be replaced, added and removed to get a string b of length n from a string a of length m. Unfortunately, the naive dynamic programming algorithm works for O (mn) ; the best minds of ShAD can do it in O (mn / log max (n, m)) ; it’s easy to think of O ((n + m) ⋅ alpha) , where alpha is the answer; science can do it for O ((alpha - | n - m |) min (m, n, alpha) + m + n) (the algorithm is simple, read at least in the ShAD) or, if a little clearer, for O (alpha ^ 2 + m + n) . There is still a minus: it is most likely impossible to get rid of quadratic time in the worst case polynomially - Peter Indik wrote a very powerful article about this.

There is an exercise: imagine that for replacing a character in the Levenshtein distance you pay a fine not two, but two; then come up with an algorithm for O ((n + m) log (n + m)) .

It still does not fit, too long and expensive. But with the help of such a distance, we did the detection of typos in the queries.

In addition to the Levenshtein distance, there is a Hamming distance. With him, too, everything is pretty bad, but a little better than with the Levenshtein distance. It does not take into account the removal of characters, but only for two lines of the same length counts the number of characters in which they differ. Therefore, if we use the distance for strings of length m <n, then only in the search for the closest substrings.

How to calculate such an array of discrepancies (an array d of n - m + 1 elements, where d [i] is the number of different characters in the i-th from the beginning of the overlay) for O (| Sigma | (n + m) log (n + m) ) ? First, do | Sigma | bit masks indicating whether the given symbol is equal to the considered one. Next, we calculate the answer for each of the Sigma masks and add - we get the original answer.

Consider an example. abba



, substring ba



, binary alphabet. We get 2 masks 1001, 01



and 0110, 10



.

    a 1001 01 - 0  01 - 0  01 - 1 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

    b 0110 10 - 0  10 - 1  10 - 1 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

We get the array [0, 1, 2] - this is almost the correct answer. But note that for each letter, the number of matches is just the scalar product of a fixed binary needle and all haystack substrings. And for this, of course, there is a fast Fourier transform!

For those who do not know: the FFT can multiply two polynomials of degrees m <n in a time O (n log n) , provided that the work with the coefficients is performed per unit time. Convolutions are very similar to scalar products. It is enough to duplicate the coefficients of the first polynomial, and expand and supplement the second with the required number of zeros, then we get all the scalar products of one binary string and all substrings of another in O (n log n) - some kind of magic! But believe me, this is absolutely real, and sometimes people do it.

But not in ClickHouse. For us, working with | Sigma | = 30 is already large, and the FFT is not the most pleasant practical algorithm for the processor, or, as they say in common people, "the constant is large."

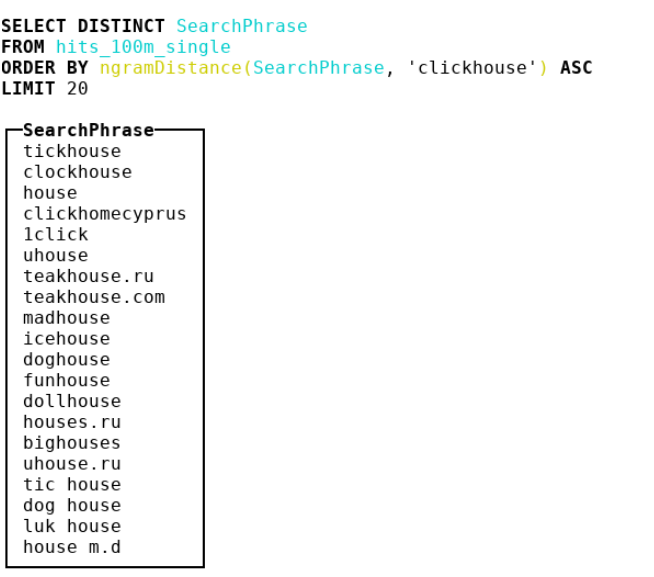
Therefore, we decided to look at other metrics. We got to bioinformatics, where people use n-gram distance. In fact, we take all the n-grams of haystack and needle, consider 2 multisets with these n-grams. Then we take the symmetric difference and divide by the sum of the powers of two multisets with n-grams. We get a number from 0 to 1 - the closer to 0, the more the lines are similar. Consider an example where n = 4 :

 abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2         . |{abcd, cdab}| / (2 + 2) = 0.5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

As a result, we made a 4-gram distance and put a bunch of ideas from SSE in there, and we also slightly weakened the implementation to double-byte crc32 hashes.

Check out the implementation . Caution: very compelling and optimized code for compilers.

I especially advise you to pay attention to the dirty hack for casting lower case for ASCII and Russian code points.

- ngramDistance(haystack, needle)



- returns a number from 0 to 1; the closer to 0, the more lines look alike.

- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (dirty hack for Russians and ASCII).

Hyperscan also does not stand still - it has functionality for approximate search: you can search for lines similar to regular expressions by Levenshtein’s constant distance. A distance + 1 automaton is created, which is interconnected by deleting, replacing or inserting a character, meaning “fine”, after which the usual algorithm for checking whether an automaton accepts a particular line is applied. In ClickHouse, we implemented them under the following names:

- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k])



- similar to multiMatchAny, only with distance.

- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k])



- similar to multiMatchAnyIndex, only with distance.

With increasing distance, the speed begins to degrade greatly, but still remains at a fairly decent level.

Finish the search and get down to processing UTF-8 strings. There was also a lot of interesting things.

UTF-8 line processing

I admit that it was difficult to break through the ceiling of naive implementations in UTF-8 encoded strings. It was especially difficult to screw SIMD. I will share some ideas on how to do this.

Recall what a valid UTF-8 sequence looks like:

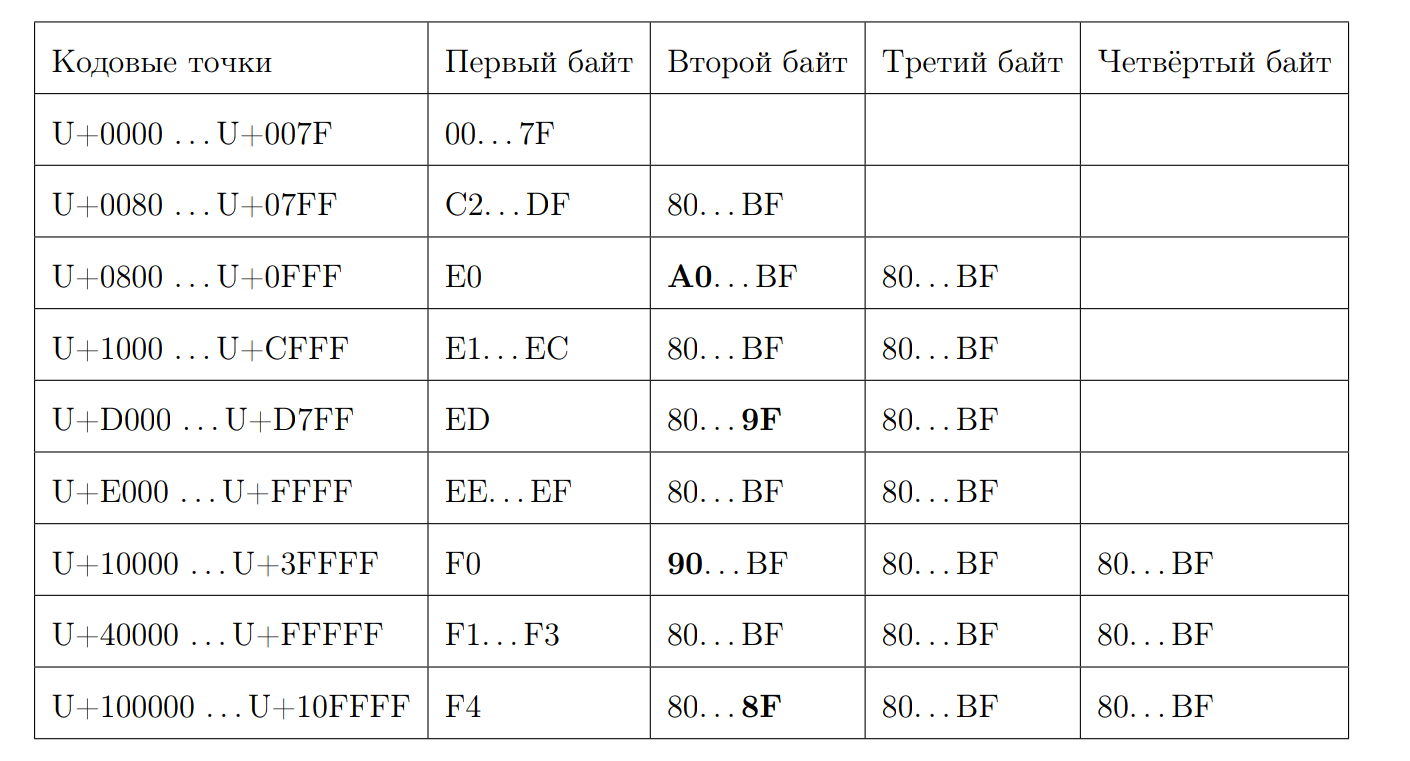
Let's try to calculate the length of the code point by the first byte. This is where bit magic begins. Again we write a few properties:

- Starting at 0xC and at 0xD have 2 bytes

- 0xC2 = 11 0 00010

- 0xDF = 11 0 11111

- 0xE0 = 111 0 0000

- 0xF4 = 1111 0 100, there is nothing further than 0xF4, but if there was 0xF8, there would be a different story

- Answer 7 minus the position of the first zero from the end, if it is not an ASCII character

We calculate the length:

 inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Fortunately, we have in stock instructions that can calculate the number of zero bits, starting with the most significant ones.

 f = __builtin_clz(val) // (bsrl,     ) f(2) = 30, f(8) = 28, f(7) = 29
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Compute bitScanReverse:

 unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Let's try to calculate the length of a UTF-8 string by code points via SIMD. To do this, look at each byte as a signed number and note the following properties:

- 0xBF = -65

- 0x80 = -128

- 0xC2 = -62

- 0x7F = 127

- all first bytes are in [0xC2, 0x7F]

- all non-first bytes are in [0x80, 0xBF]

The algorithm is quite simple. Compare each byte with -65 and, if it is greater than this number, add one. If we want to use SIMD, then this is the usual load of 16 bytes from the input stream. Then there is a byte comparison, which in case of a positive result will give the byte 0xFF, and in the case of a negative - 0x00. Then the pmovmskb



instruction, which will collect the high bits of each byte of the register. Then the number of underscores increases, we use the intrinsic for the popcnt



SSE4 instruction. The scheme of this algorithm can be illustrated by an example:

It turns out that along with the decompression, processing per core will be approximately 1.5 GB / s.

The functions are called:

- lengthUTF8(string)



- returns the length of a correctly encoded UTF-8 string, something is considered to be invalid, an exception is not thrown.

We went further because we wanted even more functions with UTF-8 string processing. For example, checking for validity and casting to a valid UTF-8 expression.

To check for validity, I took https://github.com/cyb70289/utf8/ , adapted for ClickHouse (actually just changed the processing of the tails) and got 1.22 GB / s speed compared to 900 MB / s for the naive algorithm . I will not describe the algorithm itself, it is quite complicated for perception.

- isValidUTF8(string)



- returns 1 if the string is correctly encoded with UTF-8, otherwise 0.

- toValidUTF8(string)



- replaces invalid UTF-8 characters with the (U + FFFD) character. All consecutive invalid characters collapse into one replacement character. No rocket science.

In general, in UTF-8 lines, due to the not-so-pleasant static scheme, it is always difficult to come up with something that is well optimized.

What's next?

Let me remind you that this was my thesis. Of course, I defended her at 10/10. We already went with her to Highload ++ Siberia (though it seemed to me that she was not very interested in anyone). Watch the presentation . I liked that the practical part of the thesis resulted in a lot of interesting research. And here is the diploma itself. It has a lot of typos, because no one read it. :)

As part of the preparation of the diploma, I did a bunch of other similar work (links lead to pool requests):

- Optimized concat function 2 times ;

- Made the simplest python format for requests ;

- Accelerated LZ4 by 4% ;

- I did a great job on SIMD for ARM and PPC64LE ;

- And he advised a couple of students of the FCS with diplomas in ClickHouse.

In the end, it turned out that, according to my impressions, every month Lesha tried to chant me ClickHouse is the most pleasant system for writing high-performance code, where there is documentation, comments, excellent developer and devops support. ClickHouse is awesome, really. Tired of shifting JSON formats? Come to Lesha and ask for a task of any level - he will provide it for you, and over the weekend you will get great pleasure from writing code.

But with all the achievements of ClickHouse and its design, it's probably not about them. Not primarily in them.

I went through 4 years of undergraduate studies at the FCS, in June I graduated from the HSE with a red diploma, worked for a year and a half in an awesome team in Yandex, having well pumped. Without total experience all this time and iron Nothing written in the post would work. FCN is very cool, if you take the maximum from it. Thanks to Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko, Gleb Evstropov, Max Babenko maxim_babenko for meeting in my funny adventure on FCN. And also thanks to all the teachers who taught me something.