A little more about trigonometry in computing

On Habré there were already many articles devoted to fast calculations of trigonometry, when it is strongly necessary, but I would like to supplement them with one small note with a reference to school trigonometry.

Sometimes there may be no hardware implementation of trigonometry, sometimes there may be other reasons to invent methods for speeding up the calculation.

Maths

Let's recall some simple formulas from the school course.

Let's start with the simple ones:

(one)

• sin x = cos (90° - x)
  
  
  
  
• cos x = sin (90° - x)
  
  
  
  
• sin -x = -sin x
  
  
  
  
• cos -x = cos x
  
  
  
  
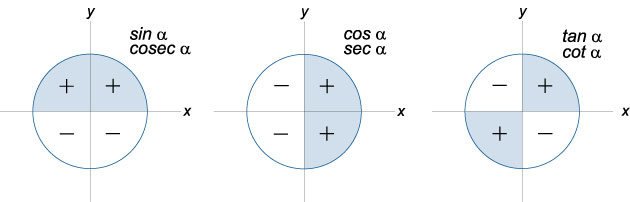
• In the general case, sin (90°N ± x) = ±cos x
  
  
  
  for odd N and ±sin x
  
  
  
  for even. The sign is taken based on the sign of the argument in the corresponding quarter of the circle.

Farther:

(2)

• cos (x + y) = cos x cos y - sin x sin y
  
  
  
  
• sin (x + y) = sin x cos y + cos x sin y
  
  
  
  

And further:

(3)

• sin x = x - x^3/3! + x^5/5! - ...
  
  
  
  
• cos x = 1 - x^2/2! + x^4/4! - ...
  
  
  
  

The cosine / sine of any angle can be reduced to an argument in the range from 0 ° to 45 ° using the formulas of the first group.

For small angles, trigonometric functions can be reduced to asymptotic expansions if the discarded terms deliberately go beyond the discharge grid.

All intermediate angles can be obtained by summing large angles with a certain step (and for them trigonometry can be considered tabular), and residues that will sooner or later give a linear decomposition.

Application

Suppose we are working with IEEE-754 single precision numbers, they have the names float, single, etc. There are 23 characters in the mantissa, so we need to get a relative error of 2^-23



.

Let's evaluate how deep you need to go down to build argument tables.

For the sine, we discard the cubic term, so we need its relation to the linear one to be less than the permissible error, which means that: 1 - (x - x^3/3!) / x = x^2/6



2/6 2 ^ -23, whence it follows that for arguments of no more than 0.000846 radians, the accuracy of the approximate calculation for the sine is enough for us. For cosine, if you drop the quadratic term, you need an accuracy of about 2 times better - 0.000488 radians.

So, we do not need to have tabular values ​​for the argument less than 0.000488 radians.

To build the table, we renormalize the input argument so that the value 0 corresponds to the angle 0 °, and for the value 1 corresponds to the angle 45 °, or pi/4=0.78539816



radians. Then the minimum angle obtained above will be converted to 0.0006217 radians, or approximately 1/1600



- this is more than 1/2048 = 2^-11



.

Next, you will need to choose the step of the tables based on how we want to distribute the calculations, we will divide the exponent 11 into several parts. For example, you can divide it into two parts: 11 = 6 + 5, then we need two tables of size 64 and 32 records (total 96), or three parts: 11 = 4 + 4 + 3 (the size of the tables is 16 + 16 + 8 = 40 entries), but there will be more multiplication operations - the specific choice will depend on the task and available resources.

Note: an entry in a table is a pair of sine and cosine arguments. If we store with single precision, then the record size is 8 bytes.

Example

Let's take the decomposition 4 + 4 + 3 as an example, and then generalize.

So, the task: calculate the value of sin x



for an arbitrary x



.

Step 1. We bring the argument x



to our scale, dividing it by the constant pi/4



(let's call it x'



).

Step 2. Depending on the value of the argument x'



using formulas (1), we select the desired function so that its argument is in the range from 0 to 1 (inclusive) (let's call x''



. At this step, you will also need to mark the sign of the result .

[suppose for example that the sine is]

Step 3. We will use the tables (I’ll remind you that there are 3 of them), while the indices in the table will be “bit fields” in the binary representation of the argument x''



- the first 4 bits after the decimal point, then 4 more, and 3 more, and the remaining ones for business bits will go to the remainder.

The table sine is called S1, S2, S3, the table cosines are C1, C2, C3.

Since we divided the angle by pi/4



, in order to get the remainder in radians, it must be multiplied by the same amount. The "bit" remainder multiplied by pi/4



is denoted by A. Then its sine will be equal to A, and the cosine - 1.

Step 4. Combine everything that happened:

 C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

|sin x| = S123 + C123 A



|sin x| = S123 + C123 A



(if you got a sine in step 2)

|sin x| = C123 - S123 A



|sin x| = C123 - S123 A



(if you received the cosine in step 2)

Step 5. If at step 2 we considered that the result should be negative, then this minus should be entered into the result.

Conclusion

A similar approach can be used both for calculating in real numbers of any size, and, for example, for implementing specialized fixed-point arithmetic. Actually, at one time it was the last task that made me dig deeper in this direction, but it was a long time ago.