Neutron stability in the atomic nucleus
The fact that baffles many of those who study the nature of ordinary matter for the first time is that the nucleus of any atom heavier than hydrogen contains both protons and neutrons, but neutrons also decay (disintegrate into other particles) on average in 15 minutes! How can the nuclei of carbon, oxygen, nitrogen, silicon be so stable if the neutrons of which they are composed cannot survive on their own?
The answer to this question turns out to be very simple after you understand how energy works: it is pure bookkeeping. But understanding energy is not easy at all. First you need to read an article about the types of energy . And before that you need to read the article about energy, momentum and mass . These concepts need to be presented before you understand the answer to a given question.
If you read an article about the interaction energy, you know that a hydrogen atom consists of a proton and an electron, which, due to the negative binding energy, are unable to escape from each other - they are locked inside the atom. The negative binding energy comes from the negative interaction energy, partially balanced by the positive energy of the electron (and a little bit - the proton). The interaction energy comes from the electron's action on the electric field near the proton (and vice versa).
In this article I will explain why the neutron is stable in the next simple atom of the atom: the deuteron, the nucleus of "heavy hydrogen" or "deuterium." A deuteron consists of one neutron and one proton - in principle, simple, and not too different from a hydrogen atom with one electron and one proton. Having understood why a neutron is stable in a deuteron, you will understand the basic principle by which neutrons can be stable inside all stable nuclei. The essence is as follows: the energy of the interaction of protons and neutrons is negative, and quite large, therefore, in some nuclei, neutron decay would lead to an increase in the energy of the system (consisting of the remnants of the nucleus after its decay and all particles emitted during the decay), which would violate the law of energy conservation. Since energy must be conserved, decay is impossible.
I will not describe the interaction of a neutron with a proton, since a strong interaction, much more complicated than the electric (and magnetic) interactions between the proton and the electron that make up the hydrogen atom, is responsible for this. This complexity is partly due to the compound nature of the interaction — it is a bit like how an electromagnetic interaction can bind two hydrogen atoms into a hydrogen molecule, although both atoms are electrically neutral. But this analogy does not cover some important details. Nuclear physics is a separate topic.

Fig. one
Fortunately, we do not need these difficulties. We need to know that these forces create a negative interaction energy for a system of proton, neutron and various complex fields that allow them to influence each other. The result is a stable deuteron. Just as a hydrogen atom cannot suddenly decay into an electron and a proton, a deuteron cannot suddenly decay into a neutron and a proton.
This does not mean that a deuteron or a hydrogen atom cannot be destroyed. You can “ionize” a hydrogen atom (knock out an electron from a proton) if you add external energy — in the form, say, of a sufficiently energetic photon. The same method can be used to break up deuterium and knock out a neutron from a proton. But energy for this needs to be obtained outside the system; neither hydrogen nor deuteron will decay independently.
Let us recall the necessary (but not sufficient) condition for the disintegration of an object — the mass of the initial object must exceed the sum of the masses of the objects into which it disintegrates. Where does this condition come from? From the law of conservation of energy. Soon we will see how and why (as usual, by mass I mean “rest mass”).
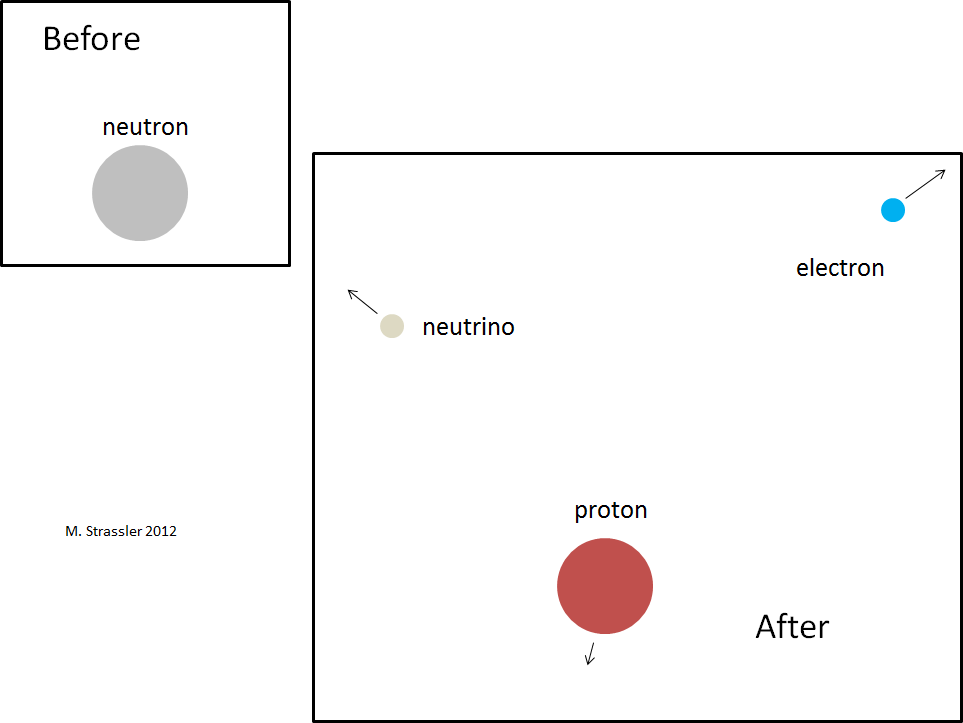
Fig. 2
Let us verify that this condition is satisfied for a neutron that can decay into a proton, electron, and electron antineutrino. The decay is shown in Figure 2; the neutron spontaneously turns into these three particles. Neutron and proton are actually larger in size than electrons and antineutrinos — although the drawing was not made to scale anyway. The diameter of a neutron or proton is about one billionth trillionths of a meter (100,000 times smaller than an atom), and it is known about the diameter of an electron or neutrino that it is at least another 1000 times smaller than this.
In fig. 3 shows energy accounting (see Fig. 1). Before the neutron decay, the energy of the entire system is equal to the mass energy (E = mc 2 ) of the neutron. The neutron mass is 0.939565 ... GeV / c 2 .
The ellipsis indicates that this is not the exact value, but so far we do not need greater accuracy. So the neutron mass energy
0.939565 ... GeV / c 2
After the neutron decay, what will the energy of the entire system be? Since energy is being saved, and no energy was received from outside, the energy of the system will be equal to the same - 0.939565 ... GeV!
But how is it distributed?
First, we will not have interaction energy. This is not obvious, but very important. When a proton, electron and antineutrino scatter, the energy of their interaction becomes negligible.
Secondly, each of the particles has energy of mass. How much is there?
• The proton mass energy is 0.938272 ... GeV.
• The electron mass energy is 0.000511… GeV.
• The mass energy of the antineutrino can be neglected, so small it is.
And this is good, since the neutrino mass is still unknown to us. We know that it is at least far less than 0.000001 GeV.
The resulting mass-energy is equal to
(0.938272 ... + 0.000511 ... + 0.000000 ...) GeV = 0.938783 ... GeV
That is less than the mass energy of the neutron, with which we started, at 0.000782 ... GeV. So far, we do not see how it is saved. The energy of the neutron mass is not completely transformed into the energy of the mass of the proton, electron and neutrino. Excess energy in fig. 3 shown in yellow.
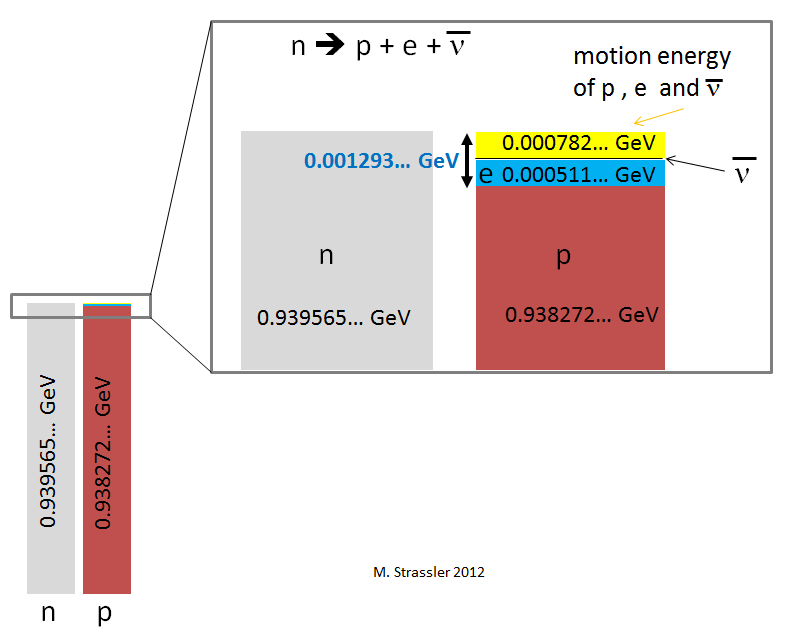
Fig. 3
The difference can be filled with the energy of motion. She is always positive. We only need to distribute the extra 0.000782 ... GeV between the particle motions so that the impulse of the system is maintained (believe me, it is possible). Then the energy will be saved, because the energy of the neutron mass has turned into the energy of mass and the energy of motion of the proton, electron and neutrino.
I did not specify the exact amount of motion energy that was sent to the proton, electron, and neutrino, since in each of the cases of neutron decay, the energy will be distributed differently, just randomly (such is quantum mechanics). Only the total motion energy will always be the same, 0.000782 ... GeV.
Let's return to the deuteron. The total energy of the deuteron, like that of the hydrogen atom, consists of the positive energy of the mass of its two components (proton and neutron), the positive energy of motion of the two components, and the negative interaction energy, more than covering the energy of motion. Moreover, as with any particle or system, the mass of the deuteron will be equal to its total energy (more precisely, the total energy that you measure when it does not move relative to you), divided by C 2 , the square of the speed of light. Accordingly, if the deuteron is resting relative to you, on the basis of its measured mass, equal to 1.875612 ... GeV / s 2 , one can say that its energy is equal to
Deuteron mass energy = 1.875612 ... GeV =
• Proton mass energy + neutron mass energy,
• The energy of motion of the proton + the energy of motion of the neutron,
• Interaction energy (negative, and more in magnitude than the energy of motion).
<proton mass energy + neutron mass energy
= 0.938272 ... GeV + 0.939565 ... GeV = 1.877837 ... GeV
Therefore, the deuteron binding energy is
1.875612 ... GeV - 1.877837 ... GeV = -0.002225 ... GeV

Fig. four
Negative binding energy means, as is the case with the hydrogen atom, that the deuteron cannot simply fall apart into a neutron and a proton, as shown in Fig. 4. It would violate the conservation of energy, stating that a decaying particle must be more massive than the particles into which it disintegrates. As shown in fig. 5, energy can not save. A neutron and a proton have more mass energy than a deuteron, and there is no source of negative energy capable of compensating the energy deficit, since there is no interaction energy between the far-separated proton and the neutron, and there is no negative movement energy. This means that the process in fig. 4 can not happen.

Fig. five
There is only one step left, and it is, compared to the previous ones, quite simple. The question is: why can't a neutron decay inside a deuteron?
Suppose it broke up: what will remain? Then we will have two protons, an electron and an antineutrino; see fig. 6. Two protons are repelled - they have a positive electric charge, and the electric force pushes them away. A strong nuclear interaction, trying to attract them together, is not as strong as that of a neutron with a proton, and the total effect of the two forces will be repulsive. As a result, this interaction will push protons apart. Meanwhile, the electron and antineutrino will also leave the scene.
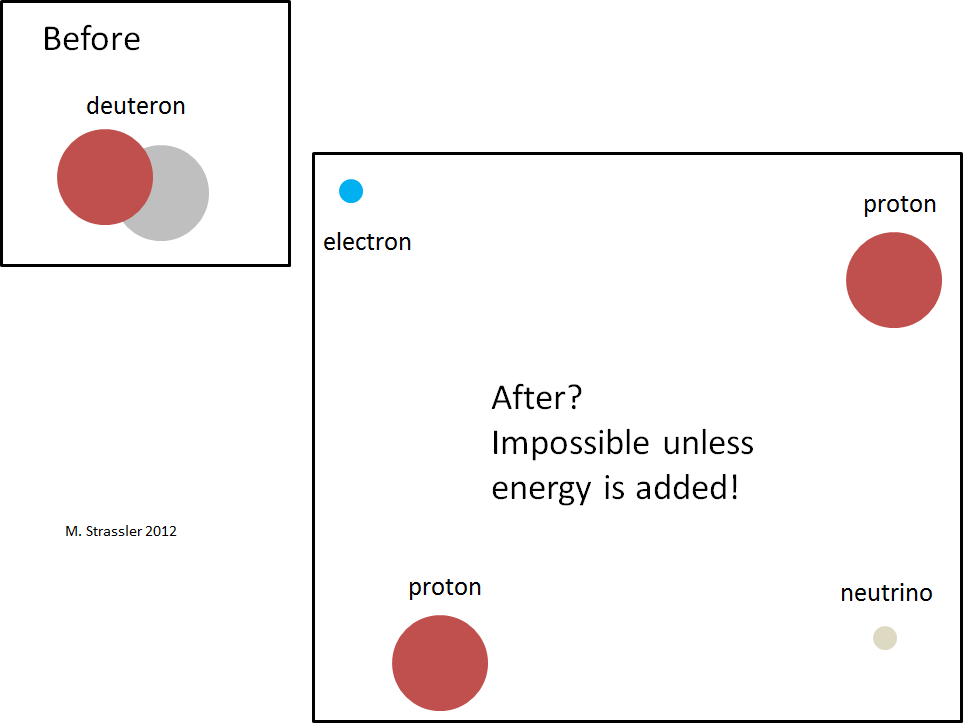
Fig. 6
When all four particles are far apart (as roughly shown in Fig. 6, but imagine that they are scattered further), there will be no significant interaction energy between them. The energy of the system will consist only of the sum of the energies of the masses of the particles and the energies of the motion. Since the energy of motion is always positive, the minimum energy that particles can have will be equal to the sum of their mass energies. But this energy is more than the mass energy of the deuteron (Fig. 7)! Even the energy of the mass of two protons, 1.876544 ... GeV, is already greater than the energy of the mass of the deuteron. And an additional 0.000511 GeV just sprinkles salt on the wound.
Therefore, the neutron inside the deuteron cannot decay; the interaction energy that holds the deuteron pulls its mass down — low enough so that the neutron decay inside the deuteron violates the conservation of energy!

Fig. 7
And so it happens with all stable nuclei in nature. But do not think that whenever you combine neutrons and protons, the result is a stable nucleus! Stable kernels are extremely rare.
If you take Z protons and N neutrons and try to make a nucleus of them, then for most Z and N variants you will fail. Most of these nuclei will instantly disintegrate, they will not form at all. Roughly speaking, the attractive force between Z protons and N neutrons is strongest when Z is approximately equal to N. On the other hand, protons are repelled from each other due to electromagnetic interaction. This force increases with increasing Z. The competition between these two effects suggests that the core is likely to be stable when Z is slightly less than N; and the more Z and N, the greater should be the difference between Z and N. This can be seen in Fig. 8. Only the nuclei marked with black are stable; they range in what is poetically called the "valley of stability."
And what are the cores, marked with color? It turns out that there are quite a few nuclei that still decay, but can live for quite a long time. Often we call such objects "unstable", and those that live long enough - "metastable". The use of words depends on the context. Neutron lives 15 minutes. There are nuclei that live for several milliseconds, days, decades, millennia, and even billions of years. These nuclei we call radioactive; these are the dangerous consequences of cases involving radiation or weapons, and the tools used in smoke detectors and for cancer control, among others.
There are a bunch of ways these nuclei can decay, but some of them decay, turning a neutron into a proton inside the nucleus. We know this by increasing the charge of the nucleus and by the fact that an electron escapes from it together with the antineutrino. Others can even decay, turning a proton into a neutron! We know about this, because the charge of the nucleus decreases, and a positron (antielectron) flies out of it. Calculations of how much a certain nucleus can live and how it will disintegrate are handled by very complex nuclear physics — I will not give a course on it here (and I am not an expert).

Fig. eight
Suffice it to say that the negative interaction energy of particles, combined with energy conservation, can change the whole game, making it impossible for certain processes that are possible under normal conditions - and vice versa.
The answer to this question turns out to be very simple after you understand how energy works: it is pure bookkeeping. But understanding energy is not easy at all. First you need to read an article about the types of energy . And before that you need to read the article about energy, momentum and mass . These concepts need to be presented before you understand the answer to a given question.
If you read an article about the interaction energy, you know that a hydrogen atom consists of a proton and an electron, which, due to the negative binding energy, are unable to escape from each other - they are locked inside the atom. The negative binding energy comes from the negative interaction energy, partially balanced by the positive energy of the electron (and a little bit - the proton). The interaction energy comes from the electron's action on the electric field near the proton (and vice versa).
In this article I will explain why the neutron is stable in the next simple atom of the atom: the deuteron, the nucleus of "heavy hydrogen" or "deuterium." A deuteron consists of one neutron and one proton - in principle, simple, and not too different from a hydrogen atom with one electron and one proton. Having understood why a neutron is stable in a deuteron, you will understand the basic principle by which neutrons can be stable inside all stable nuclei. The essence is as follows: the energy of the interaction of protons and neutrons is negative, and quite large, therefore, in some nuclei, neutron decay would lead to an increase in the energy of the system (consisting of the remnants of the nucleus after its decay and all particles emitted during the decay), which would violate the law of energy conservation. Since energy must be conserved, decay is impossible.
I will not describe the interaction of a neutron with a proton, since a strong interaction, much more complicated than the electric (and magnetic) interactions between the proton and the electron that make up the hydrogen atom, is responsible for this. This complexity is partly due to the compound nature of the interaction — it is a bit like how an electromagnetic interaction can bind two hydrogen atoms into a hydrogen molecule, although both atoms are electrically neutral. But this analogy does not cover some important details. Nuclear physics is a separate topic.

Fig. one
Fortunately, we do not need these difficulties. We need to know that these forces create a negative interaction energy for a system of proton, neutron and various complex fields that allow them to influence each other. The result is a stable deuteron. Just as a hydrogen atom cannot suddenly decay into an electron and a proton, a deuteron cannot suddenly decay into a neutron and a proton.
This does not mean that a deuteron or a hydrogen atom cannot be destroyed. You can “ionize” a hydrogen atom (knock out an electron from a proton) if you add external energy — in the form, say, of a sufficiently energetic photon. The same method can be used to break up deuterium and knock out a neutron from a proton. But energy for this needs to be obtained outside the system; neither hydrogen nor deuteron will decay independently.
Neutron can decay
Let us recall the necessary (but not sufficient) condition for the disintegration of an object — the mass of the initial object must exceed the sum of the masses of the objects into which it disintegrates. Where does this condition come from? From the law of conservation of energy. Soon we will see how and why (as usual, by mass I mean “rest mass”).

Fig. 2
Let us verify that this condition is satisfied for a neutron that can decay into a proton, electron, and electron antineutrino. The decay is shown in Figure 2; the neutron spontaneously turns into these three particles. Neutron and proton are actually larger in size than electrons and antineutrinos — although the drawing was not made to scale anyway. The diameter of a neutron or proton is about one billionth trillionths of a meter (100,000 times smaller than an atom), and it is known about the diameter of an electron or neutrino that it is at least another 1000 times smaller than this.
In fig. 3 shows energy accounting (see Fig. 1). Before the neutron decay, the energy of the entire system is equal to the mass energy (E = mc 2 ) of the neutron. The neutron mass is 0.939565 ... GeV / c 2 .
The ellipsis indicates that this is not the exact value, but so far we do not need greater accuracy. So the neutron mass energy
0.939565 ... GeV / c 2
After the neutron decay, what will the energy of the entire system be? Since energy is being saved, and no energy was received from outside, the energy of the system will be equal to the same - 0.939565 ... GeV!
But how is it distributed?
First, we will not have interaction energy. This is not obvious, but very important. When a proton, electron and antineutrino scatter, the energy of their interaction becomes negligible.
Secondly, each of the particles has energy of mass. How much is there?
• The proton mass energy is 0.938272 ... GeV.
• The electron mass energy is 0.000511… GeV.
• The mass energy of the antineutrino can be neglected, so small it is.
And this is good, since the neutrino mass is still unknown to us. We know that it is at least far less than 0.000001 GeV.
The resulting mass-energy is equal to
(0.938272 ... + 0.000511 ... + 0.000000 ...) GeV = 0.938783 ... GeV
That is less than the mass energy of the neutron, with which we started, at 0.000782 ... GeV. So far, we do not see how it is saved. The energy of the neutron mass is not completely transformed into the energy of the mass of the proton, electron and neutrino. Excess energy in fig. 3 shown in yellow.

Fig. 3
The difference can be filled with the energy of motion. She is always positive. We only need to distribute the extra 0.000782 ... GeV between the particle motions so that the impulse of the system is maintained (believe me, it is possible). Then the energy will be saved, because the energy of the neutron mass has turned into the energy of mass and the energy of motion of the proton, electron and neutrino.
I did not specify the exact amount of motion energy that was sent to the proton, electron, and neutrino, since in each of the cases of neutron decay, the energy will be distributed differently, just randomly (such is quantum mechanics). Only the total motion energy will always be the same, 0.000782 ... GeV.
Deuteron is stable
Let's return to the deuteron. The total energy of the deuteron, like that of the hydrogen atom, consists of the positive energy of the mass of its two components (proton and neutron), the positive energy of motion of the two components, and the negative interaction energy, more than covering the energy of motion. Moreover, as with any particle or system, the mass of the deuteron will be equal to its total energy (more precisely, the total energy that you measure when it does not move relative to you), divided by C 2 , the square of the speed of light. Accordingly, if the deuteron is resting relative to you, on the basis of its measured mass, equal to 1.875612 ... GeV / s 2 , one can say that its energy is equal to
Deuteron mass energy = 1.875612 ... GeV =
• Proton mass energy + neutron mass energy,
• The energy of motion of the proton + the energy of motion of the neutron,
• Interaction energy (negative, and more in magnitude than the energy of motion).
<proton mass energy + neutron mass energy
= 0.938272 ... GeV + 0.939565 ... GeV = 1.877837 ... GeV
Therefore, the deuteron binding energy is
1.875612 ... GeV - 1.877837 ... GeV = -0.002225 ... GeV

Fig. four
Negative binding energy means, as is the case with the hydrogen atom, that the deuteron cannot simply fall apart into a neutron and a proton, as shown in Fig. 4. It would violate the conservation of energy, stating that a decaying particle must be more massive than the particles into which it disintegrates. As shown in fig. 5, energy can not save. A neutron and a proton have more mass energy than a deuteron, and there is no source of negative energy capable of compensating the energy deficit, since there is no interaction energy between the far-separated proton and the neutron, and there is no negative movement energy. This means that the process in fig. 4 can not happen.

Fig. five
The neutron inside the deuteron cannot decay
There is only one step left, and it is, compared to the previous ones, quite simple. The question is: why can't a neutron decay inside a deuteron?
Suppose it broke up: what will remain? Then we will have two protons, an electron and an antineutrino; see fig. 6. Two protons are repelled - they have a positive electric charge, and the electric force pushes them away. A strong nuclear interaction, trying to attract them together, is not as strong as that of a neutron with a proton, and the total effect of the two forces will be repulsive. As a result, this interaction will push protons apart. Meanwhile, the electron and antineutrino will also leave the scene.

Fig. 6
When all four particles are far apart (as roughly shown in Fig. 6, but imagine that they are scattered further), there will be no significant interaction energy between them. The energy of the system will consist only of the sum of the energies of the masses of the particles and the energies of the motion. Since the energy of motion is always positive, the minimum energy that particles can have will be equal to the sum of their mass energies. But this energy is more than the mass energy of the deuteron (Fig. 7)! Even the energy of the mass of two protons, 1.876544 ... GeV, is already greater than the energy of the mass of the deuteron. And an additional 0.000511 GeV just sprinkles salt on the wound.
Therefore, the neutron inside the deuteron cannot decay; the interaction energy that holds the deuteron pulls its mass down — low enough so that the neutron decay inside the deuteron violates the conservation of energy!

Fig. 7
Other atomic nuclei
And so it happens with all stable nuclei in nature. But do not think that whenever you combine neutrons and protons, the result is a stable nucleus! Stable kernels are extremely rare.
If you take Z protons and N neutrons and try to make a nucleus of them, then for most Z and N variants you will fail. Most of these nuclei will instantly disintegrate, they will not form at all. Roughly speaking, the attractive force between Z protons and N neutrons is strongest when Z is approximately equal to N. On the other hand, protons are repelled from each other due to electromagnetic interaction. This force increases with increasing Z. The competition between these two effects suggests that the core is likely to be stable when Z is slightly less than N; and the more Z and N, the greater should be the difference between Z and N. This can be seen in Fig. 8. Only the nuclei marked with black are stable; they range in what is poetically called the "valley of stability."
And what are the cores, marked with color? It turns out that there are quite a few nuclei that still decay, but can live for quite a long time. Often we call such objects "unstable", and those that live long enough - "metastable". The use of words depends on the context. Neutron lives 15 minutes. There are nuclei that live for several milliseconds, days, decades, millennia, and even billions of years. These nuclei we call radioactive; these are the dangerous consequences of cases involving radiation or weapons, and the tools used in smoke detectors and for cancer control, among others.
There are a bunch of ways these nuclei can decay, but some of them decay, turning a neutron into a proton inside the nucleus. We know this by increasing the charge of the nucleus and by the fact that an electron escapes from it together with the antineutrino. Others can even decay, turning a proton into a neutron! We know about this, because the charge of the nucleus decreases, and a positron (antielectron) flies out of it. Calculations of how much a certain nucleus can live and how it will disintegrate are handled by very complex nuclear physics — I will not give a course on it here (and I am not an expert).

Fig. eight
Suffice it to say that the negative interaction energy of particles, combined with energy conservation, can change the whole game, making it impossible for certain processes that are possible under normal conditions - and vice versa.
All Articles