効率的なグラフ画像のセグメンテーション

画像のセグメント化とエッジ検出 （ エッジ検出 ）は、 コンピュータービジョンシステムで重要な役割を果たし、シーンの認識とオブジェクトの選択（定義）に使用されます。 概して、これは、たとえば高レベルのタスクを解決するために設計された並べ替えと同じツールです。 したがって、このクラスのアルゴリズムの設計を理解することは、そのようなシステムを構築するときに、要件（品質/パフォーマンスの点で）とタスクの詳細を考慮して不要ではありません。



この記事では 、2004年に公開されたPedro F. Felzenszwalb （ MIT ）およびDaniel P. Huttenlocher （ Cornell University ）による効率的なグラフベースの画像セグメンテーションアルゴリズムについて簡単に説明します。 はい、アルゴリズムは比較的古いですが、それにもかかわらず、それはまだ非常に人気があり、パフォーマンスの面で良い結果を示しています。



カットの下-写真とテキストの大規模な混合物、主題の現在のレベルの知識を要求しません。 好奇心は大歓迎です。







最初に、画像処理とはほとんど関係のないグラフについて、一見アルゴリズムを説明します。 ただし、少し後に画像のセグメンテーションに関連して解釈が行われます。

クラスカルアルゴリズム

Kraskalアルゴリズム （ wiki ）は、ワイヤフレーム（特定のグラフの最小スパニングツリー）を構築します。 次に、英語の略語MST （最小スパニングツリー）が使用されます。



目的：マップ上にはいくつかの集落があり（複数の連絡先がボード上にあります）、それらをすべて相互に接続して、道路（ワイヤ）の全長が最小になるようにする必要があります。









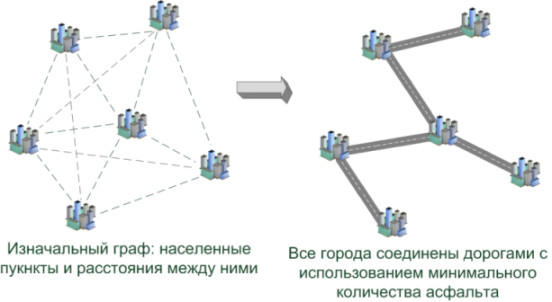
* はい、そのような定式化のタスクは通常「シュタイナー問題」（ 記事 ）と呼ばれ、それを解決して、都市をさらに安く接続することができます。 しかし、最終的には、アスファルトを舗装しないでください... =）



それを解決するには、次のものが必要です。

• グラフ ：それが何であるか、コードでどのように表されるかについて簡単に説明しましたが、Habréで既に述べられています（ 記事 ）
• Kraskalのアルゴリズム （ wiki ）：この定式化の問題を解決するための主要な「エンジン」。 これは、Leysersonの聖書「アルゴリズム：構築と分析」（ 本 ）のCormenに非常によく記述されています。
• Disjoint-set data structure （ wiki ）：上記のアルゴリズムを効率的に実行するために必要な追加の構造。 どのように機能するかは同じ聖書で説明されていますが、名前は少し異なります（ メモリを変更しない場合：Union Find-Setなど ）

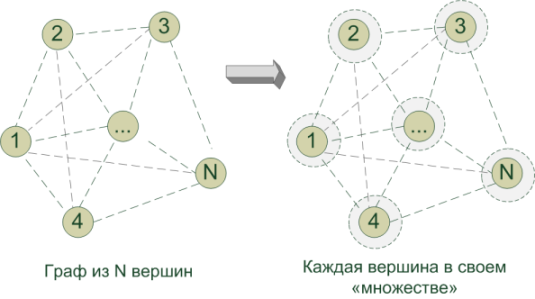
問題の現在のステートメントでは、グラフの頂点（v _i ） -都市を表し、エッジe（v _i 、v _j ） -都市間の道路を表します。 都市のペア（v _i 、v _j ）間の距離を知っています-これはエッジw（e（vi、vj））の重みです。 MSTを見つける必要があります。 グラフ内のこのようなツリー（サイクルなし：余分な道路を建設する理由）により、エッジの合計が最小になり、すべての頂点に到達できます。



最初は、各頂点（都市）自体が、対応するセットG ₁ 、G ₂ 、... G _N （頂点の数による）の唯一の誇り高い代表です。 彼女がMSTを結成したと考えながらみましょう。 アルゴリズムの過程で、これらの異種集合すべてを効率的かつ外交的に組み合わせて単一のGにし、それに含まれる頂点がMSTを形成するようにします。 これを行うには：

• グラフ内のすべてのエッジを、長さの増加順に並べます（道路）
• rib骨に沿って長さの昇順に走り、rib骨の端e =（a、b）を見ます：
  • 頂点（ aおよびb ）が同じセットに属している場合 ：そのため、それらはすでにサブMSMSの一部の教育されたサブセットに参加しているため、エッジの合計はすでに最小になっています。 そのようなエッジはスキップされます-私たちはそれを必要としません そうでなければ、それは木にサイクルを形成し、アスファルトを無駄にします
  • 頂点（ aおよびb ）が micro-MSTの異なるサブセットに属している場合 ：結合する必要があります。 両方のサブセットを1つに結合（マージ）する、最小長のエッジ（道路）が見つかりました。 より短い長さのすべてのリブはすでに考慮されており、このリブよりも安くそれらを結合することはできません。 このようなエッジは、MSTツリーの構築に使用されるエッジのリストに記録され、セットは1つに結合されます
  • グラフのすべての頂点が存在する目的のMSTに等しい単一のセットを取得するまで、結合サイクルを続けます
• 単一の頂点セット （MST）と、それを結合するために使用されるエッジのリストを取得します 。これは、すべての頂点を結合する最小全長のツリーです。

ばらばらのデータ構造

Kraskalアルゴリズムで「セット」の概念を実装するには、 Disjoint-setデータ構造が使用されます。 それを使用する作業は、2つの基本操作を実行するように最適化されています。

• 現在属している頂点を見つけます
• これらのセットをすばやく1つにまとめる

画像のセグメンテーションのトピックに近づくために、画像のピクセルとその色に関する説明を続けます。 日本の青い海を背景にバッジーを分割するとします。 最初に、各ピクセル（グラフの上部）はそれ自身-独自のセグメント（セット）にありますが、アルゴリズム中に「類似」色（1つのオブジェクト）のピクセル（頂点）は徐々に1つのセグメントに結合されます。



アルゴリズムの特定のステップで、2つの隣接するピクセルを接続するエッジが接続されると仮定します。エッジの一方の端では、ピクセルは「オレンジ」で、もう一方は「赤」です。 エッジの長さは、ピクセル間の「色差」として定義されます。 短い長さのリブ（類似の色）はすべて既に結合されています。バッジーのオレンジと赤のセグメントは、おそらくすでに強調表示されています。 アルゴリズムに従って、現在の「オレンジ」ピクセルと「赤」ピクセルが同じセグメントにあるかどうかを調べる必要がありますか？ それらが異なっていて、セグメントの色が似ていると思われる場合は、それらを1つに組み合わせて構築を続けます...一般に、ピクセルのみで同じクラスカルアルゴリズム。



これらの操作に使用される構造は、ツリーに非常に似ています（ただし、インデックスの配列によって実装されます）。 その中で、各ピクセルに対して、祖先が示されています。 同じセグメントにある同様の色のピクセルへのポインター（インデックス）。 基本操作：

• ピクセル「x」の セグメントを検索します 。先祖に沿って最上部に移動します。 一番上のピクセルはツリーのルートであり、現時点ではこのセグメントの「代表」です。
• セグメントの結合 。 ピクセルが異なる「代表」を持つ場合、それらは異なるセグメントに属します。そうでなければ、1つのルートがあります。 それらを結合するために、ツリーの高さを増やさないように、より低い高さ（最も遠いピクセルからルートまで）のセグメントの「代表者」が、より長い「代表者」に参照されます。 これで、共通の代表者を含む結合セグメントが作成されました。
• 次回ピクセルからルートまで遠くまで走らないように、「代表」が正常に検出された後、ピクセルから直接リンクを確立します。 これは、次の検索のパスを短縮し、「 パス圧縮 」と呼ばれます。

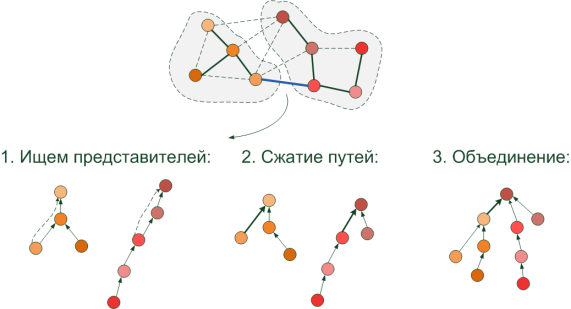
さて、ピクセル単位でセグメントを効率的に検索して結合し、Kraskalアルゴリズムを使用してMSTを構築できるようになりました。 2つの領域を結合または分離する決定がどのように行われるかを調べる時が来ました。

分割して征服する

セグメンテーションアルゴリズムは、1つのセグメントが終了し、別のセグメントが開始する場所を明確に決定する必要があります。 原則として、境界線は、オブジェクトの背景、飛行機の影、オウムの海、フェンスの碑文の領域で見られる明るさおよび/または色合いの特徴的な違いです...そして「差」がいくつかの「しきい値」（しきい値）よりも大きい場合、これは、これらが異なるセグメントであることに従う必要があります。 しかし、小さな問題があります。違いはオブジェクトごとに大きく異なり、一意に定義された（定数）しきい値（しきい値）でセグメントを「分離」することは困難です。 テーブルの表面が壁に接している場合：テーブルの表面（壁）に沿った隣接するピクセル間の差は比較的小さくなりますが、テーブルと壁の境界では、セグメントを分離するジャンプがあります。 これは明らかです。 そして、海の背景にオウムがいるとしたら？ 彼自身は非常に「雑多」で、その中には海からそれを「分離」するために強度に大きな違いがあります（緑赤黄…）、別の「閾値」（閾値）が必要です。 そして徐々に、隣接するセグメントが「一緒に運命づけられていない」と判断するしきい値は、ローカルインジケータだけでなく、1つのエッジ（隣接するピクセルを接続する）に沿った強度差だけでなく、これらのセグメント自体も依存する必要があるという結論に達しますそれ自体は滑らか（色の点で）または「カラフル」です。

灰色の写真

本格的なカラー画像の処理に進む前に、画像がグレースケール、すなわち 画像行列の各セルには、ピクセルの明るさを表す数値が間隔[0 ... 1]に格納されます。

効率的なグラフベースの画像セグメンテーション

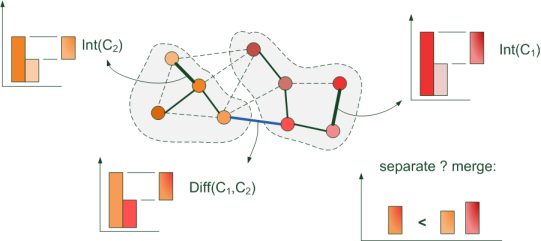
各画像ピクセルは、グラフの頂点で表されます。 そして、隣接する頂点を接続するエッジの重み（長さ）は、次の式で表されます。w（v _i 、v _j ）= | I（p _i ）-I（p _j ）| ここで、 I（p _i ）はピクセルp _iの強度（明るさ）です。



Kraskalアルゴリズムの実行中に、中間段階でいくつかの異なるセグメント（ピクセルのサブセット）があり、内部のエッジの合計重量が最小になります。セグメントは最小長のエッジで結合されます。 隣接するピクセル間の「強度の差」は最小限です。 したがって、同じセグメント内の隣接するピクセルの色は似ています。 しかし、最大rib骨の特定の値（強度差）までのみ...



そして...現在のステップで最小のエッジを取りました。 このエッジの隣接する頂点である2つのピクセルについて、1つの（既に構築された）セグメントから決定しますか？

• はい 、1つのセグメントから：アルゴリズムの実行を継続します。
• いや セグメントが画像内の同じオブジェクトの一部を表すのか、それらを結合する必要があるのか​​、またはそれらの強度が「大幅に」異なるのかを判断する必要がありますか？

セグメント間の差を決定するために、すでに特定の値を構築した各セグメントに関連付けます-その内部の最大強度差、すなわち セグメント内のMSTの最長エッジ：







個別に検索する必要はありません。「サブセグメント」のコンポーネントを結合するときに追加されるエッジの長さを保存するだけです。 実際、合併時には、追加されたエッジの長さは、各「サブセグメント」の既に構築されたMSTよりも長くなりました。 エッジは昇順で処理されます。



セグメントC ₁ 、C _2の近似決定ルールを取得します。

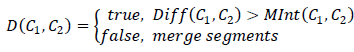
	症状：これらのセグメントを区別する必要がありますか？
	2つの異なるセグメントを接続する最小長の現在のエッジ
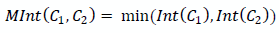	考慮されたセグメントの1つ内のより小さい（大きいから）強度差

セグメントが「結合」するためには、それらの境界での強度の差は、結合された各セグメント内の最大差よりも小さくなければなりません。

あなたを探しています

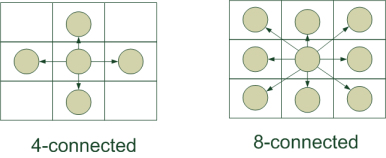
画像からグラフを作成する方法は？ どのピクセルが隣接していますか？ 表面には2つの主なアプローチがあります。

• 4-connected ：各ピクセルは、上/下/左/右から隣接するピクセルに接続されます。 このような構造は、グラフ内のエッジの数が最小限であるという点で魅力的です。
• 8-connected ：前のオプションに加えて、各ピクセルを斜めに位置する隣接ピクセルに接続します。 したがって、グラフにはより多くのエッジがあり、アルゴリズムの実行はやや遅くなります。 しかし、結果のセグメンテーションはより良いはずです-ピクセル間のより多くの関係が考慮されるためです。

このアルゴリズムは、8連結グラフではより良い結果をもたらすはずですが、4連結グラフでは非常に受け入れられる結果が得られると同時に、はるかに高速に実行されます。 そして、カラー画像を処理するための「距離」として、アルゴリズムの作成者によって実装された、まさにそのような単純なピクセルの色の違いを取ることができます。







ただし、このような距離の定式化には欠点があります。 局所的に隣接するピクセル間の「強度の違い」を考慮すると、次の写真の空はワイヤーを横切る2つの別々のセグメントに分割されます。または、グリッドの背景に対して芝生を処理すると、さらに悪い結果が得られます。









芝生の各フラグメントは個別のセグメントとしてマークされますが、これは1つのオブジェクトです！



したがって、代替の実施形態では、著者は、近くのピクセルだけでなく、画像の局所特性（すぐ近くにあるピクセル）を考慮して、「ワイヤーを飛び越え」（写真を参照）、一定の距離にあるセグメントの続きに手を伸ばそうとすることを提案します。 これを行うには、ピクセルの位置（x、y）とその色（r、g、b）の両方に応じて、エッジ長としてユークリッド距離を選択することをお勧めします。







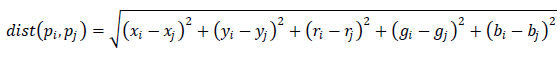
物理的にある程度の距離にある場合でも、ピクセルが近くにある場合、または類似の色相を持つ場合、ピクセルは「隣接」と見なされます。 グラフを作成するために、著者は、各ピクセルを10（20、30）「最も近い」接続することを提案しています。 これにより、セグメンテーションが改善されますが、より多くのコンピューティングリソースが必要になります。

団結して、チーム！

最初に戻ります。 むかしむかし、すべてのピクセルが断片化されると、隣接するピクセル間で強度の有意差が観察され、それらのマージが妨げられました。 各ピクセルを分離する必要のある顕微鏡写真が与えられた可能性はほとんどありません。おそらく、それらは何らかの大きなオブジェクト（オウム）の一部です。 パーティションの正確性がより重要である、すでに構築されている大きなセグメントよりも「マージ」（マージ）の程度が大きいため、決定ルールで構築されたセグメントのサイズに応じて値を追加します。 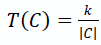どこ| C | 問題のセグメントのパワー（現時点でのピクセル数）であり、 kは既に手動で設定されたセグメンテーションパラメーターです。 決定ルールの同様の修正により、式が使用されます。









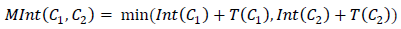
「修正」は、セグメントの成長に応じて徐々に平準化されます（増加| C | ）...



実際、このようなタスクTの代わりに、処理された画像の詳細を考慮する別の関数を選択できます：セグメントの形状、写真内の位置、特定の色合い...

ガウスぼかし

非常に「雑多な」写真に戻る：









「強度の差」などの定義でピクセル間の距離を決定するとき、「雑多」のピクセルは、単一のオブジェクトであっても、1つのオブジェクトに結合するのに非常に柔軟ではないことは明らかです。 ノイズ/アーティファクトの結合と除去をより「調整」するために、通常、特定の半径（標準偏差） シグマのガウスフィルター（http://habrahabr.ru/blogs/webdev/43895/）が画像に適用されます。 これは、ピクセルの色成分の「相互浸透」を引き起こし、ピクセルはより積極的に接触します。

合計

セグメンテーションには多くの方法があります。さまざまなアプローチについては、 記事 「画像のセグメンテーション方法：自動セグメンテーション」で詳しく説明されています 。 しかし、概して、セグメンテーションは高品質または生産的である必要があり、運がよければ、一度にすべてを行う必要があります。 上記の方法は、単なる生産的なオプションです。



このセグメンテーションの方法では、最も時間のかかるプロセスは、 O（e log⁡e）に対して実行されるすべてのエッジのソートです。ここで、 eはグラフ内のエッジの数です。 したがって、NxM画像の場合、エッジのピクセルは次のようになります： | e | = 4 * N * M



アルゴリズムのソースコードは、このリンクから入手できます。

しかし、OpenCVはどうでしょうか？

誰もが好きなOpenCVライブラリ（ wiki ）には、「 cvPyrSegmentation 」メソッドがあります。 ピラミッド画像セグメンテーション法。 配置が多少異なります。 したがって、彼の説明には別の記事、つまり写真が必要です。 セグメントはレイヤー（レベル）に組み込まれ、同様の色のピクセルを1つ（レイヤーの上にある）に結合し、「ストップ」の上の次のレベル（レベル）にあるレイヤーを順番に処理します。









2006年、マラガ大学（スペイン）で、いくつかのピラミッド型アルゴリズムが比較され、その結果が次の記事に示されています。









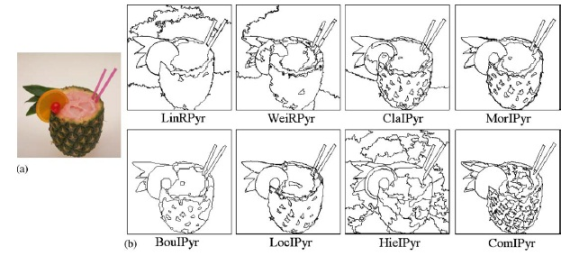
著者は、8つの方法のうち3つが注目に値するという結論に達しました。そのため、画像をオブジェクトに分割するためにかなり高品質の結果が得られます。 ただし、ピラミッド型アルゴリズムの実行時間は0.5秒からです。 最大4.5秒 （Pentium 766 MHzで256x256ピクセル）、「 効率的なグラフベースの画像セグメンテーション 」は、「1秒未満 」の著者によると実行されます。 私たちでは、 1024x768の写真は、「入れ子人形」内で0.5秒 （U9400 2 x 1.4GHz）でうまくいきました：VMWare-Matlab-mex（C ++）。 一般に、ピラミッド型-品質、記事で説明されているグラフ-速度。 どちらにも生命権があります。 =）





最も熱心な読者には、「魔法の泡」の秘密を明らかにします。写真にはどのような数字が表示されますか？ これらは「 セグメンテーション（シグマ、k、最小） 」メソッドのパラメーターであり、そのうち2つはすでによく知っています。3番目の「 最小 」は強制的な最小セグメントサイズであり、「小さな」セグメントはありません。









頑張って



PSあまり蹴らないようにお願いします。これは、Habréの9回目の投稿です。