量子コンピューティングがソフトウェア開発に与える影響

みなさんこんにちは！



約6か月間、出版社は量子コンピューティングとその実用性のトピックに積極的に取り組んできました。 長い間、この興味深いトピックに関する翻訳にふさわしい記事を見つけることは、そのような記事がOracleブログに掲載されるまで不可能でした。 この出版物は、この新しいパラダイムのソフトウェア、ハードウェア、および純粋に自然科学の問題の優れた紹介となるので、読むことは必須です。







過去数か月および数年にわたって、量子コンピューティングへの関心は著しく高まってきました。 この分野での画期的な成果について語る研究機関、企業、または州組織から新しい資料が絶えず登場しています。 同時に、技術的根拠の弱い記事は量子コンピューティングの潜在的な結果について議論しており、予測は最新の暗号化技術のハッキングから、すべての病気を治し、本格的なAIを作成することへの取り組みに至るまでさまざまです。 ただし、これらの期待のすべてが等しく現実的ではありません。



あなたが実践的な地味なプログラマーなら、これらの計算で事実とフィクションの境界がどこにあるのか、そして量子コンピューティングが将来のソフトウェア開発にどのように影響するのか疑問に思うかもしれません。



当然、量子コンピューティング用の実用的なハードウェアが作成されるまでには、何年もかかります。 ただし、このパラダイムの一般原則は今日すでに理解されており、シミュレータを使用して量子コンピューティングの可能性を実現するアプリケーションを開発者が作成できるようにする抽象化があります。

量子コンピューティングは別のCPUゲインに削減されますか？

従来のコンピューターを使用した従来のソフトウェア開発では、高レベルのプログラミング言語（Javaなど）を多数の（ハードウェア）トランジスターで実行される操作に変換します。



図1では、このプロセスは最も単純な形式で図式化されています。Javaソースコードはプラットフォームに依存しないバイトコードにコンパイルされ、プラットフォーム固有のマシンコードに変換されます。 マシンコードは、メモリ内で実行されるいくつかの単純な操作（ゲート）を使用します。 この目的で使用される主なハードウェアコンポーネントは、よく知られているトランジスタです。







図 1.高度なプログラミング言語のトランジスタで実行される操作への翻訳 。



近年達成された生産性の向上は、主にハードウェア技術の改善により達成されました。 単一のトランジスタのサイズは大幅に縮小し、各平方ミリメートルに配置できるトランジスタが増えるほど、コンピュータのメモリと処理能力が増えます。



量子コンピューティングは破壊的な技術です。なぜなら、ここで最も単純なコンピューティングユニットは古典的なトランジスタではなく、量子ビットであり、これについては以下で説明します。



ポイントは、これらの主要な要素の違いだけでなく、バ​​ルブの異なるデバイスにもあります。 したがって、Fig。 量子コンピューティングの1は適用されません。

量子コンピューティングは、スタック全体をJavaレベルまで分割しますか？

要するに-「そうでもない」。 科学者たちは、量子コンピューターが特定の問題を解決するのに特に適している一方で、他の問題は従来のコンピューターを使用してより合理的に解決されることに徐々に同意しています。 おなじみですね。 GPUとCPUを比較すると、同様の状況が観察されます。 GPUではトランジスタも使用されますが、原理的にはCPUとは異なりますが、高級言語で記述された多くのアプリケーションは、CPUとGPUの両方の機能を内部で使用します。 GPUはベクトル処理に非常に優れており、多くのアプリケーションやライブラリでは、CPUとGPUの動作が区別されています。



たとえば、これはまさにJavaFXまたはDeeplearning4jを使用する場合の状況です。 JavaFXを使用するユーザーインターフェイスを使用してアプリケーションを作成する場合、Javaコードのみを使用します（ユーザーインターフェイスを宣言するためにFXMLを使用することもあります）。 JavaFXシーンを画面に表示する必要がある場合、内部JavaFX実装はこれにシェーダーとテクスチャを使用し、図2に示すように低レベルGPUドライバーに直接接続します。したがって、CPUの操作に適したコードの部分とGPUを使用します。







図 2. JavaFXはGPUとCPUの作業を委任します。



図に示すように。 2、JavaFX実装コードデリゲートは、GPUおよびCPUに渡すことで動作します。 これらの操作は開発者からは隠されていますが（APIからは提供されません）、より強力なJavaFXアプリケーションを開発する必要がある場合、GPUの特定の知識が役立つことがよくあります。



Deeplearning4jを使用すると、同様の状況が発生します。 Deeplearning4jには、必要なベクトルおよび行列演算を実行するための実装がいくつかあり、それらのいくつかはGPUを使用します。 ただし、コードが使用する容量（CPUまたはGPU）が最終開発者であるかどうかは関係ありません。



量子コンピューターは、通常、問題の量が増えると指数関数的に増加する問題を解決する優れた仕事をするようであり、したがって、古典的なコンピューターではほとんど解決できないか、ほとんど解決できないようです。 特に、専門家はハイブリッドの実施形態について話します。典型的なエンドツーエンドのアプリケーションには、CPUで実行される古典的なコードが含まれますが、量子コードも含まれる場合があります。

システムはどのようにして量子コードを実行できますか？

今日、量子コンピューターのハードウェアはまだ非常に実験的です。 大企業や、おそらくいくつかの州はプロトタイプの開発に従事していますが、そのような技術は広く利用できません。 しかし、表示されるとき、その形状は異なる場合があります。

• 量子コプロセッサーは、システム内のCPUと統合できます。
• 量子問題は、量子クラウドシステムに委任できます。

そのような決定の実際的な背景については非常に不確実性が残っていますが、量子コードがどのように見えるべきかについてますます同意しています。 最下位レベルには、次のブリックが必要です。 キュービットと量子ゲート 。 それらに基づいて、予想される動作を実装する量子シミュレーターを作成できます。



したがって、量子シミュレータはそのような開発に理想的なツールです。

量子コンピューターの実際の機器で得られる結果とほぼ同じ結果になるはずですが、量子機器を加速する量子効果は従来のソフトウェアを使用してシミュレートする必要があるため、シミュレーターの動作は非常に遅くなります。

量子コンピューティングの基本的な構成要素は何ですか？

多くの場合、古典的な計算と量子計算を比較することが重要です。 古典的な計算では、ビットとゲートがあります。



ビットには1ビットの情報が含まれ、その値は0または1です。

バルブは1つ以上のビットに作用し、それらを操作できます。 たとえば、図3に示すNOTゲートは、ビットの値を反転します。 入力が0の場合、NOTゲートの出力は1になり、逆も同様です。







図 3. NOTバルブ



量子コンピューティングでは、同等のビットとゲートがあります。 ビットの量子等価物はキュービットです。 量子ビットの値は、古典的なビットのように0または1に等しくすることができますが、いわゆる重ね合わせにすることもできます。 これは複雑な概念であり、キュービットは同時に0と1の両方の状態になります。



量子ビットが重ね合わせられている場合、その値は状態0と1の線形結合です。これは図に示すように記述できます。 4：







図 4.量子ビットが重ね合わせられている場合の平等。



注：量子ビットは多くの場合、 ブラケット表記で記述されます。変数名は文字「|」の間に配置されます。 および「>」。



図の式 4は、量子ビットxが状態| 0>と| 1>の重ね合わせにあることを報告します。 これは、状態| 0>または状態| 1>であることを意味しません。 これは、彼の現在の状態が私たちに知られていないことを意味します。



実際には、同時に両方の状態にあり、この形式では操作できます。 ただし、キュービットを測定すると、| 0>または| 1>のいずれかの状態になります。 上記の式には別の制限があります：a ^ 2 + b ^ 2 = 1。

aとbの値は確率的です：量子ビットを測定するとき、x ^が値| 0>を含む確率a ^ 2と、測定された量子ビットが値| 1>を含む確率b ^ 2があります。



量子コンピューティングの楽しさを打ち消す重要な制限要因があります。キュービットが測定されると、キュービットが配置された潜在的な重ね合わせに関するすべての情報が失われます。 キュービット値は0または1です。



計算では、重ね合わせのキュービットは、0と1に同時に対応できます（異なる確率で）。 2つのキュービットがある場合、それらを使用して4つの状態（00、01、10、および11）を表すことができます。 ここで、量子コンピューターの力の本質に迫ります。 8つのクラシックビットがあるため、0〜255の範囲で1つの数値を正確に表すことができます。8ビットのそれぞれの値は0または1です。

1つの状態のみを測定できる場合、重ね合わせの使用は何ですか？

多くの場合、アルゴリズムの結果は単純（「はい」または「いいえ」）ですが、それに到達するには、多くの並列計算が必要です。 計算中にキュービットを重ね合わせて保持すると、さまざまなオプションをすぐに考慮することができます。 個々の組み合わせごとに決定を行うことなく、量子コンピューターはすべてのオプションを1ステップで計算できます。

次に、多くの量子アルゴリズムで、次の重要な段階が始まります。アルゴリズムの結果を、意味のある結果をもたらす測定値に結び付けることです。 多くの場合、干渉が考慮されます。興味深い結果は構造的に互いに重なり合いますが、関心のない結果は互いに相殺されます（破壊的干渉）。

どうすればキュービットを重ね合わせ状態に「変換」できますか？

古典的なゲートがビットを操作するように、量子ゲートはキュービットを操作します。 いくつかの量子ゲートは古典的なものに似ています。 たとえば、Pauli-Xゲートは、量子ビットを状態a | 0> + b | 1>から状態b | 0 |に転送します。 + a | 1>、これは古典的なNOTゲートの原理に似ています。 実際、a = 1およびb = 0の場合、キュービットは最初は状態| 0>でした。 パウリ-Xバルブの動作後、このキュービットは図1に示すように状態| 1>になります。 5。







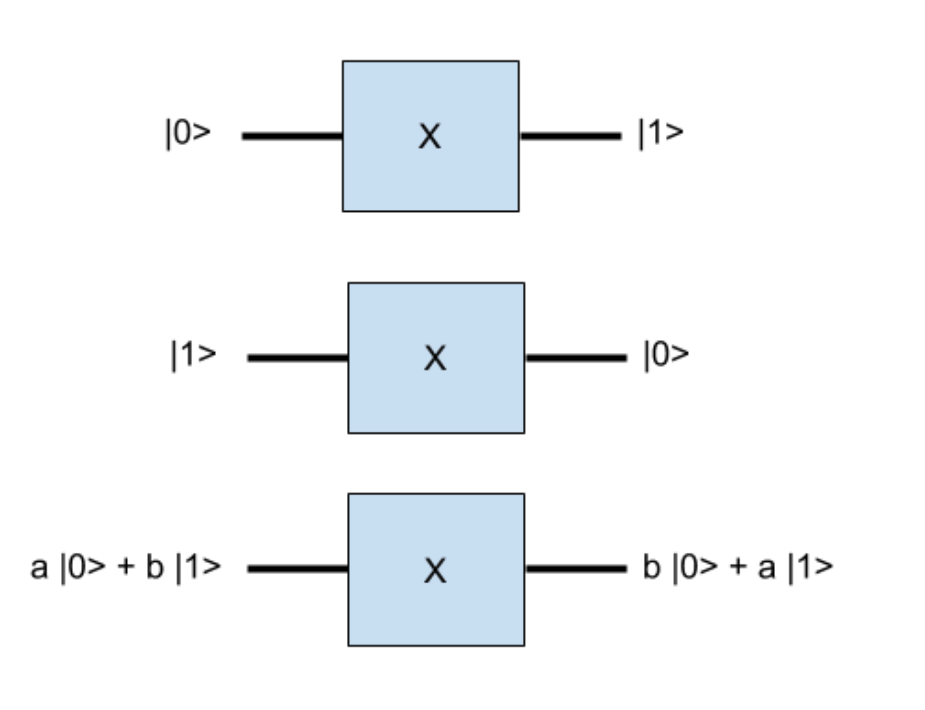
図 5. Pauli-Xバルブを使用した結果。



この文脈では、アダマール弁は非常に興味深いです。 図に示すように、キュービットを状態| 0>：1 / sqrt（2）*（| 0> + | 1>）に重ね合わせます。 6。







図 6.アダマールバルブを適用した結果。



アダマールバルブをキュービットに適用してキュービットを測定すると、キュービット値が0になる確率が50％、キュービット値が1になる確率が50％になります。キュービットが測定されるまで、重ね合わせ状態のままです。 。

これはどのように可能ですか？

この質問の答えに本当に興味がある場合は、量子物理学を詳細に研究する必要があります。 しかし、幸いなことに、これらの現象の理論的な基礎全体は必要ありません。 重ね合わせの現象は理解できないように見えるかもしれませんが、自然界の素粒子に特徴的なのはこれらの特性であることを強調することが重要です。 したがって、量子コンピューティングは、一見すると思われるよりも、物理的現実の基本にはるかに近いものです。

数年待ってから、量子コンピューティングを詳しく見てみましょう。

いや この場合、遅れます。 理論的には、最初にハードウェアを開発し、次にソフトウェアレベルの調査に進み、それで何が達成できるかを確認することができます。 しかし、すべての概念はすでに多かれ少なかれ明確であり、Java、C＃、Pythonなどを含む一般的な言語で量子シミュレータを作成することはすでに可能です。

次に、これらのシミュレーターを使用して、量子アルゴリズムを処理できます。 これらのアルゴリズムは、実際の量子機器で作業する際にそれらの助けを借りて達成可能なパフォーマンスの向上をもたらすことはありませんが、機能的には完全に完成するはずです。



したがって、現在量子アルゴリズムを開発している場合は、それを改善する時間があり、量子機器が利用可能になったときに開始できます。



量子アルゴリズムには、従来のアルゴリズムとは異なる知的アプローチが必要です。 著名な科学者が前世紀に量子アルゴリズムの開発を開始し、整数の乗算、リストの検索、パスの最適化などに関するアルゴリズムを説明する記事が増えています。



今日、量子コンピューティングを行う価値がある理由は他にもあります。 現代の大企業でソフトウェアシステムをリファクタリングすることは、一晩でできることの1つではありません。 ただし、量子コンピューティングが真の革命を起こす分野の1つは暗号化です。 結局のところ、古典的なコンピューターでは大きな整数を素因数に分解することはほとんど不可能であるという理論に基づいています。



量子因数分解の問題を簡単に解決できるほど量子コンピューターが大きくなるまでには何年もかかる場合がありますが、開発者はシステムを変更して新しい安全なテクノロジーを導入するのに何年もかかることを知っています。

Javaで量子アルゴリズムを使用する方法を学習するにはどうすればよいですか？

Javaのオープンソース量子コンピューターシミュレーターであるStrangeをダウンロードしてマスターできます。 ストレンジでは、一連のキュービットを作成し、それらにいくつかの量子ゲートを適用することにより、量子アルゴリズムをシミュレートできます。



簡単な例として、q [0]とq [1]の2つのキュービットを作成して、最初は両方が状態0になるようにします。次に、各キュービットに2つの単純なゲートを適用します。 7。



最初のキュービットは最初にPauli-Xバルブに行き、次にアダマールバルブに行きます。 Pauli-Xバルブは状態| 0＆gtから| 1＆gtに変換し、アダマールバルブはそれを等しい確率| 0＆gtおよび| 1＆gtの重ね合わせに変換します。 したがって、シーケンス全体を1000回実行し、このサイクルの最後に最初のキュービットを1000回測定すると、平均して500ケースでは値0、500ケースでは値1になると予想できます。



2番目のキュービットはさらに単純です。 量子ビットの振る舞いを変更しないIdentityゲートから開始し、それをPauli-Xゲートに渡し、その値を0から1に変更します。







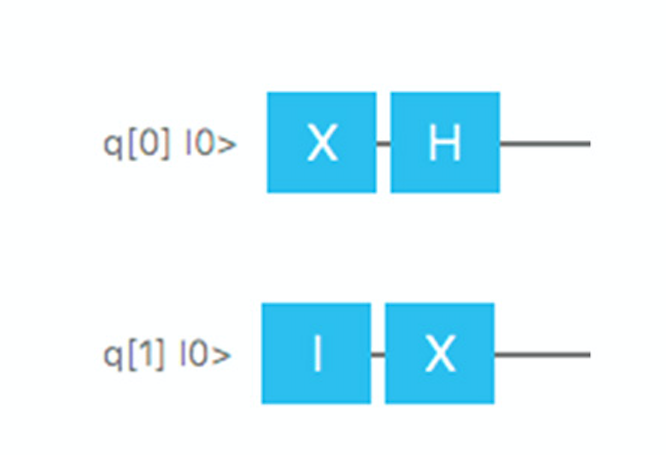
図 7. Strangeを使用してシミュレートできる量子アルゴリズムの例。



推論が正しいことを確認するために、Strangeを使用して簡単な量子プログラムを作成できます。

public static void main(String[] args) { Program p = new Program(2); Step s = new Step(); s.addGate(new X(0)); p.addStep(s); Step t = new Step(); t.addGate(new Hadamard(0)); t.addGate(new X(1)); p.addStep(t); SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment(); Result res = sqee.runProgram(p); Qubit[] qubits = res.getQubits(); Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure())); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアプリケーションでは、2つのキュービットを持つ量子プログラムが作成されます。

  Program p = new Program(2);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このプログラムの一環として、2つの段階を経ます。 最初のステップでは、Pauli-Xバルブをq [0]に適用します。 q [1]にバルブを適用しないため、Identityバルブで機能することを意味します。 このステップをプログラムに追加します。

  Step s = new Step(); s.addGate(new X(0)); p.addStep(s);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に第2段階に進み、q [0]にアダマールバルブを適用し、q [1]にパウリXバルブを適用します。 このステップをプログラムに追加します。

  Step t = new Step(); t.addGate(new Hadamard(0)); t.addGate(new X(1)); p.addStep(t);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、プログラムの準備ができました。 さあ、やってみましょう。 量子シミュレータはStrangeに組み込まれていますが、Strangeはクラウドサービスを使用して、たとえばOracle Cloudなどのクラウドでプログラムを実行することもできます 。



次の例では、簡単な組み込みシミュレータを使用してプログラムを実行し、結果のキュービットを取得します。

  SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment(); Result res = sqee.runProgram(p); Qubit[] qubits = res.getQubits();
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

量子ビットを測定する（およびすべての情報を失う）前に、確率を表示します。 次に、キュービットを測定し、値を確認します。

 Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアプリケーションを実行すると、次の出力が得られます。



qubit with probability on 1 = 0.50, measured it gives 1

qubit with probability on 1 = 1, measured it gives 1





注意：最初のキュービットについては、予想どおり値0も測定できます。

このプログラムを何度も実行すると、最初のキュービットの値は、平均してケースの半分で0、ケースの半分で1になります。

量子コンピューティングについて知る必要があるのはそれだけですか？

もちろん違います。 ここでは、いくつかの重要な概念には触れませんでした。特に、物理的には非常に遠く離れていても、2つのキュービット間の相互作用を保証する複雑さについては説明しませんでした。 最も有名な量子アルゴリズム、特に整数を素因数に分解できるショアアルゴリズムについては説明しませんでした。 また、いくつかの数学的および物理的事実も無視しました。特に、重ね合わせ| x> = a | 0> + b | 1>では、aとbの両方が複雑になる可能性があることを考慮しませんでした。



ただし、この記事の主な目的は、量子コンピューティングの印象を与え、それらがソフトウェア開発の将来にどのように適合するかを理解することでした。