高速フーリエ変換（FFT）は、最も重要な信号処理およびデータ分析アルゴリズムの1つです。 コンピューターサイエンスの正式な知識がなくても何年も使用していました。 しかし、今週私は、FFTがどのように離散フーリエ変換をこれほど迅速に計算するのか不思議に思わなかったことに思いつきました。 アルゴリズムに関する古い本のほこりを振り払い、それを開いて、J。W. CooleyとJohn Tukeyが1965年のこのトピックに関する古典的な研究で説明した、一見単純な計算上のトリックを喜んで読んだ。
この投稿の目的は、Cooley-Tukey FFTアルゴリズムに飛び込み、それに至る対称性を説明し、実際に理論を適用するいくつかの単純なPython実装を示すことです。 この研究が、私などのデータ分析の専門家に、私たちが使用しているアルゴリズムの内部で何が起こっているかについての全体像を提供することを願っています。
離散フーリエ変換
FFTは高速です
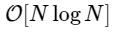直接計算される離散フーリエ変換（DFT）を計算するアルゴリズム 
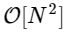。 より一般的なフーリエ変換の連続バージョンと同様に、DFTには直接形式と逆形式があり、次のように定義されます。
直接離散フーリエ変換（DFT）：
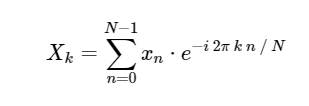
逆離散フーリエ変換（ODPF）：
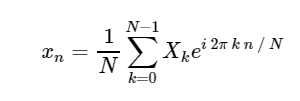
xn → Xk
からの変換は、構成空間から周波数空間への変換であり、信号のパワースペクトルの調査と、より効率的な計算のための特定のタスクの変換の両方に非常に役立ちます。 天文学と統計に関する私たちの将来の本の第10章で実際にこのいくつかの例を見つけることができます。また、Pythonで画像とソースコードを見つけることもできます。 FFTを使用して複雑な微分方程式の統合を単純化する例については、私の投稿「Pythonでのシュレディンガー方程式の解法」を参照してください。
Pythonの多くの領域でFFTの重要性（以下、同等のFFT-高速フーリエ変換を使用できます）のため、計算するための多くの標準ツールとシェルが含まれています。 NumPyとSciPyの両方には、非常によくテストされたFFTPACKライブラリのシェルがあり
scipy.fftpack
それぞれサブモジュール
numpy.fft
と
scipy.fftpack
ます。 私が知っている最速のFFTはFFTWパッケージにあります。これはPythonでもPyFFTWパッケージから入手できます。
ただし、当面は、これらの実装を脇に置き、PythonでFFTをゼロから計算する方法を考えてみましょう。
離散フーリエ変換計算
簡単にするために、逆変換も非常によく似た方法で実装できるため、直接変換のみを扱います。 上記のDFTの式を見てみると、これは単純な線形演算にすぎないことがわかります。つまり、行列にベクトルを掛けることです。
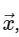
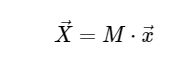
与えられた行列M
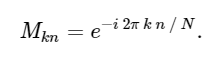
これを念頭に置いて、次のように単純な行列乗算を使用してDFTを計算できます。
[1]で：
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
numpyに組み込まれたFFT関数と比較することで、結果を再確認できます。
[2]で：
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]：
True
アルゴリズムの遅さを確認するために、これら2つのアプローチの実行時間を比較できます。
[3]で：
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
このような単純化された実装では、1000倍以上遅くなります。 しかし、これは最悪ではありません。 長さNの入力ベクトルの場合、FFTアルゴリズムは次のようにスケーリングします。
遅いアルゴリズムは 
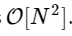。 これは、 
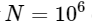要素の場合、FFTは約50ミリ秒で完了しますが、遅いアルゴリズムには約20時間かかります！
それでは、FFTはどのようにしてこのような加速を実現しますか？ 答えは対称性を使用することです。
離散フーリエ変換の対称性
アルゴリズムの構築における最も重要なツールの1つは、問題の対称性の使用です。 問題の一部が他の部分に単純に関連していることを分析的に示すことができる場合、サブ結果を1回だけ計算し、この計算コストを節約できます。 CooleyとTukeyは、FFTを受信するときにこのアプローチを使用しました。
の意味について尋ねることから始めます
。 上記の式から：
ここで、恒等式exp [2πin] = 1を使用しました。これは、任意の整数nを保持します。
最後の行は、DFTの対称性をよく示しています。
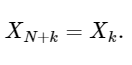
簡単な拡張
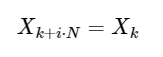
任意の整数iに対して。 以下で見るように、この対称性を使用してDFTをはるかに高速に計算できます。
FFTでのDFT：対称性の使用
CooleyとTukeyは、FFT計算を2つの小さな部分に分割できることを示しました。 DFTの定義から：
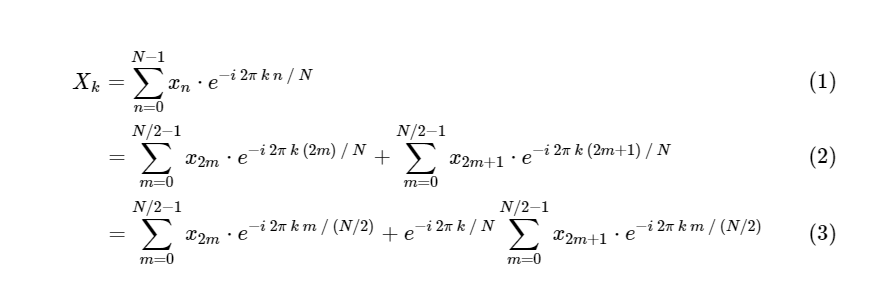
1つの離散フーリエ変換を2つの項に分割しました。これらの用語自体は、より小さな離散フーリエ変換に非常によく似ています。1つは奇数の値、もう1つは偶数の値です。 ただし、これまでのところ、計算サイクルは保存していません。 各項は（N / 2）∗ N計算、合計で構成されます
。
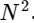トリックは、これらの各条件で対称性を使用することです。 kの範囲は0≤k<Nであり、nの範囲は0≤n<M≡N/ 2であるため、上記の対称性の特性から、各サブタスクの計算の半分しか実行する必要がないことがわかります。 私たちの計算
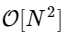になっています 
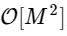ここで、MはNの2倍です。
しかし、これにこだわる理由はありません：小さいフーリエ変換のMが偶数である限り、この「分割統治」アプローチを、計算コストが半分になるたびに、配列が十分に小さくなり戦略が利益をもたらさなくなるまで再適用できます。 漸近的な制限では、この再帰的アプローチはO [NlogN]としてスケーリングします。
この再帰アルゴリズムは、サブタスクのサイズが非常に小さくなると、遅いDFTコードから始めて、Pythonで非常に迅速に実装できます。
[4]で：
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32: # this cutoff should be optimized return DFT_slow(x) else: X_even = FFT(x[::2]) X_odd = FFT(x[1::2]) factor = np.exp(-2j * np.pi * np.arange(N) / N) return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd])
ここで、アルゴリズムが正しい結果を与えることを簡単に確認します。
[5]で：
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
アウト[5]：
True
このアルゴリズムと低速バージョンを比較してください。
-[6]：
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
計算は直接バージョンよりも高速です！ さらに、再帰アルゴリズムは漸近的です
：高速フーリエ変換を実装しました。
numpyビルトインFFTアルゴリズムの速度にまだ近づいていないことに注意してください。これは予想されることでした。
fft
numpyの背後にあるFFTPACKアルゴリズムは、長年の改良と最適化を受けたFortran実装です。 さらに、NumPyソリューションには、Pythonスタックの再帰と多くの一時配列の割り当ての両方が含まれており、計算時間が長くなります。
Python / NumPyで作業するときにコードを高速化するための優れた戦略は、可能な限り繰り返し計算をベクトル化することです。 これを行うことができます-プロセスで、再帰関数呼び出しを削除します。これにより、Python FFTがさらに効率的になります。
ベクトル化されたNumpyバージョン
上記のFFTの再帰的実装では、再帰の最低レベルで、 N / 32個の同一の行列ベクトル積を実行します。 これらの行列ベクトル積を単一の行列行列積として同時に計算すると、アルゴリズムの有効性が高まります。 後続の各再帰レベルで、ベクトル化できる反復操作も実行します。 NumPyはこのような操作で優れた仕事をします。この事実を使用して、ベクトル化された高速フーリエ変換を作成できます。
[7]で：
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0]) / X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel()
アルゴリズムは少し不透明ですが、1つの例外を除いて、再帰バージョンで使用される操作の再配置にすぎません。係数の計算に対称性を使用し、配列の半分のみを構築します。 繰り返しますが、関数が正しい結果を与えることを確認します。
[8]で：
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
アウト[8]：
True
アルゴリズムがより効率的になると、より大きな配列を使用して時間を比較し、
DFT_slow
残すことができます。
[9]で：
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
実装を大幅に改善しました！ 数十行の純粋なPython + NumPyを使用して、FFTPACKベンチマークから約10倍離れました。 これはまだ計算の一貫性はありませんが、読みやすさの点では、PythonバージョンはFFTPACKソースコードよりもはるかに優れています。
では、FFTPACKはこの最後の加速をどのように実現しますか？ 基本的に、それは詳細な簿記の問題です。 FFTPACKは、再利用可能な中間計算の再利用に多くの時間を費やします。 不規則なバージョンには、過剰なメモリ割り当てとコピーが含まれています。 Fortranなどの低レベル言語では、メモリ使用量の制御と最小化が簡単です。 さらに、Cooley-Tukeyアルゴリズムは、2以外のサイズのパーティションを使用するように拡張できます（ここで実装したものは、2に基づいたCooley-Tukey Radix FFTと呼ばれます）。 畳み込みデータに基づく根本的に異なるアプローチを含む、他のより複雑なFFTアルゴリズムも使用できます（たとえば、BlueshteinアルゴリズムとRaiderアルゴリズムを参照）。 上記の拡張機能と方法の組み合わせにより、サイズが2のべき乗ではない配列でも、非常に高速なFFTを実行できます。
純粋なPythonの関数は実際にはおそらく役に立たないでしょうが、FFTベースのデータ分析の背景で何が起こっているのかについての洞察を提供してくれることを期待しています。 データの専門家として、私たちはアルゴリズム志向の同僚によって作成された基本的なツールの「ブラックボックス」の実装に対処できますが、データに適用する低レベルアルゴリズムについて理解が深まるほど、より良いプラクティスになると強く信じていますします。
この投稿はすべてIPython Notepadで作成されました。 完全なノートブックはここからダウンロードするか、 ここから静的に表示できます 。
多くの人は、この資料が新しいものとはほど遠いことに気付くかもしれませんが、私たちのように、非常に重要です。 一般に、記事が有用かどうかを書きます。 あなたのコメントを待っています。