👋🏻 🔈 👴🏻 カオスの情報エントロピー 👳 👃🏼 🔓

はじめに

エントロピーの概念を議論するHabrの出版物はたくさんありますが、ここではそれらのほんの一部を紹介します[1÷5]。出版物は読者に好意的に受け取られ、大きな関心を呼びました。出版物の著者によって与えられたエントロピーの定義[1]を与えるだけで十分です：「エントロピーは、システムについて知らない情報の量です。」 Habrのカオス現象に関する出版物でも十分です[6–9]。ただし、両グループの出版物におけるエントロピーとカオスの関係は考慮されていません。

これは、知識のさまざまな領域がカオスのさまざまなタイプの尺度を区別するという事実によるものです。

情報提供;
熱力学;
微分;
文化的。

カオス対策は、これらの領域の1つであっても非常に困難な場合でも、その特異性を考慮して記述されます。

タスクをできるだけ単純化するために、点マッピングの形式のダイアグラムとこれらの領域のエントロピー係数のグラフの秩序からカオスへの通過領域の類似性の例を使用して、情報エントロピーとカオスの関係を検討することにしました。

これから来たものは、猫の下を見ることによって学びます。

秩序からカオスへの移行のメカニズム

実際のシステムとさまざまなモデルにおける秩序からカオスへの移行のメカニズムの分析により、カオスへの移行の比較的少数のシナリオの普遍性が明らかになりました。カオスへの移行は、分岐図の形式で表すことができます（「分岐」という用語は、システムの定性的な再配置を意味し、その動作の新しいレジームの出現を意味します）。

予測不能モードへのシステムのエントリは、次々に続く分岐のカスケードによって記述されます。分岐のカスケードにより、2つのソリューション、次に4つのソリューションのいずれかが順番に選択され、システムは、可能な値の数を連続して2倍にする混chaとした乱流モードで振動し始めます。

周期倍化の分岐と、ポイントマッピングにおけるカオスの出現を考慮します。表示は、システムパラメータの次の値の以前の値への依存性を示す関数です。

x_{n + 1} = f （ x_{n} ） = l a m b d a x_{n} （ 1 - x_{n} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$

2番目によく使用される関数も考えてみましょう。

x_{n + 1} = f （ x_{n} ） = l a m b d a c d o t x_{n} c d o t （ 1 - x_{n}^{2} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

ポイントマッピングを使用して、オブジェクトは連続ではなく離散時間で研究されます。ディスプレイに移行すると、調査中のシステムの寸法が小さくなる場合があります。

外部パラメータ\ lambdaを変更すると、ポイントマッピングはかなり複雑な動作を示し、十分に大きな\ lambdaでカオスになります。カオスは、位相空間での軌道の非常に速い後退です。

分岐は、映画の定性的な再構築です。分岐が発生する制御パラメーターの値は、臨界値または分岐値と呼ばれます。

図を作成するには、次の2つのリストを使用します。

1番機能の場合：

x_{n + 1} = f （ x_{n} ） = l a m b d a x_{n} （ 1 - x_{n} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$

プログラムリスト

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

No. 2.機能用

x_{n + 1} = f （ x_{n} ） = l a m b d a c d o t x_{n} c d o t （ 1 - x_{n}^{2} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

プログラムリスト

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

ロジスティック関数の性質が重要な値に与える影響を評価するには

\ラ ム ダ

$\ラムダ$ 関数を持つ図を考える

x_{n + 1} = f （ x_{n} ） = l a m b d a x_{n} （ 1 - x_{n} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ これを行うには、リスト1を使用します。

0 <\ lambda <1の場合

l a m b d a = $ 0.9

$\ lambda = $ 0.9$ x0 = 0.47ダイアグラムを取得します：

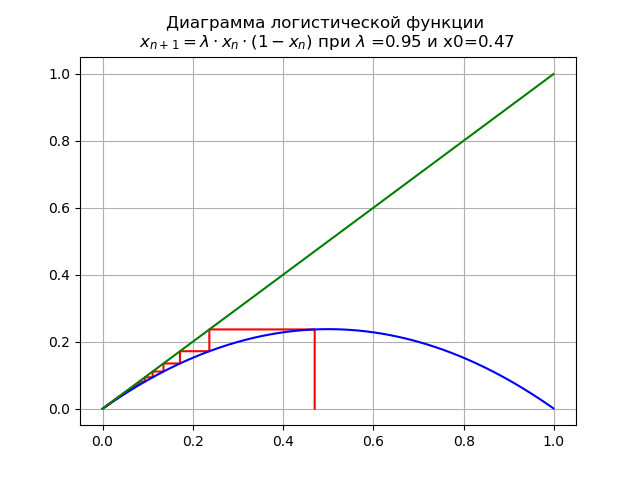
この場合、マップには単一の固定点があります

x^{*} = 0

$x ^ {*} = 0$

持続可能です。

で

1 < l a m b d a < 3

$1 <\ lambda <3$ のために

l a m b d a = $ 2.

$\ lambda = $ 2.$ x0 = 0.7ダイアグラムを取得します：

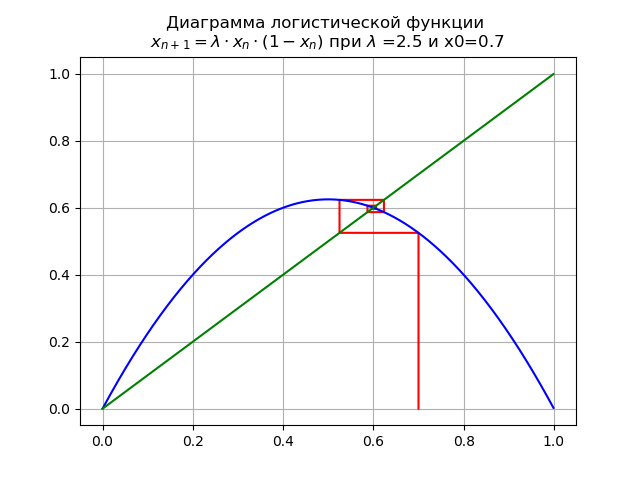
間隔[0、1]に、別の固定不動点が表示されます

x_{1}^{*} = 1 - 1 / \ラ ム ダ

$x_ {1} ^ {*} = 1-1 / \ラムダ$

で

1 < l a m b d a < 3

$1 <\ lambda <3$ のために

l a m b d a = $ 2.

$\ lambda = $ 2.$ x0 = 0.01ダイアグラムが得られます：

不動点

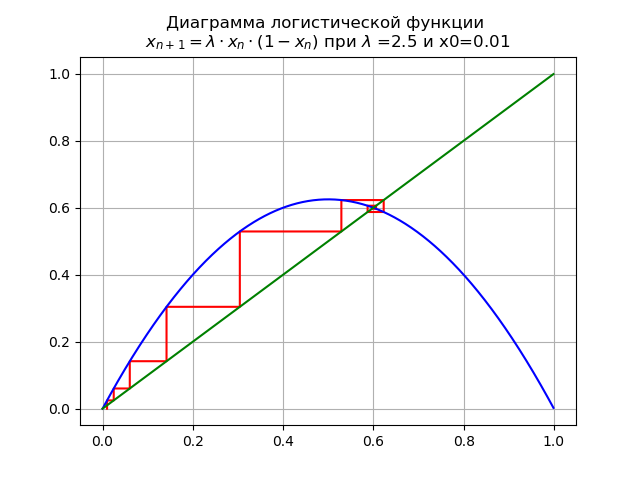
x^{*} = 0

$x ^ {*} = 0$ 安定性を失います。

で

3 < l a m b d a < 3.45

$3 <\ lambda <3.45$ のために

l a m b d a = $ 3.4

$\ lambda = $ 3.4$ そして、x0 = 0.7でダイアグラムが得られます：

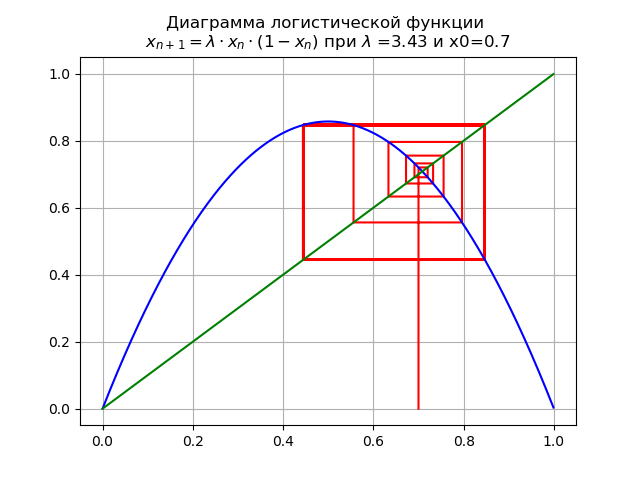
マッピングは分岐します：固定小数点

x_{1}^{*}

$x_ {1} ^ {*}$ 不安定になり、代わりに二重サイクルが表示されます。

で

3.45 < l a m b d a < 4.0

$3.45 <\ lambda <4.0$ のために

\ラ ム ダ = $ 3.5

$\ラムダ= $ 3.5$

x0 = 0.2ダイアグラムが得られます：

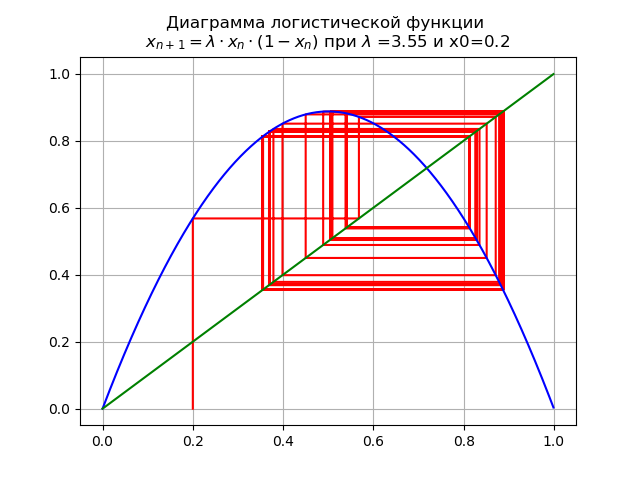
パラメーターを渡すとき

\ラ ム ダ

$\ラムダ$ スルーバリュー

\ラ ム ダ = 3.45

$\ラムダ= 3.45$ 、2倍サイクルは4倍以上になります。

最終値で

\ラ ム ダ = 4

$\ラムダ= 4$ システムには、可能なすべての注文の不安定なサイクルがあります。

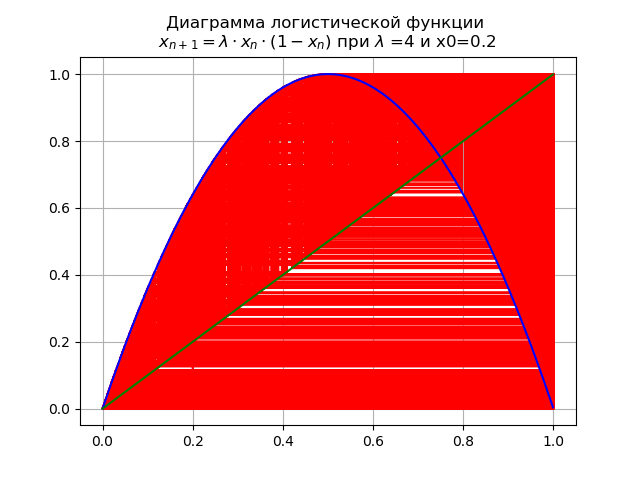
ロジスティック関数の性質が重要な値に与える影響を評価するには

\ラ ム ダ

$\ラムダ$ 関数を持つ図を考える

x_{n + 1} = f （ x_{n} ） = l a m b d a c d o t x_{n} c d o t （ 1 - x_{n}^{2} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$ 、このためにリスト2を使用します。

で

0 < l a m b d a <= 1.0

$0 <\ lambda <= 1.0$ のために

\ラ ム ダ = 0.5

$\ラムダ= 0.5$ およびx0 = 0.2：

マッピングには単一の固定小数点があります

x^{*} = 0

$x ^ {*} = 0$ 持続可能です。

で

1 < l a m b d a <= 1.998 . . .

$1 <\ lambda <= 1.998 ...$ のために

l a m b d a = $ 1.

$\ lambda = $ 1.$ およびx0 = 0.55：

ポイント

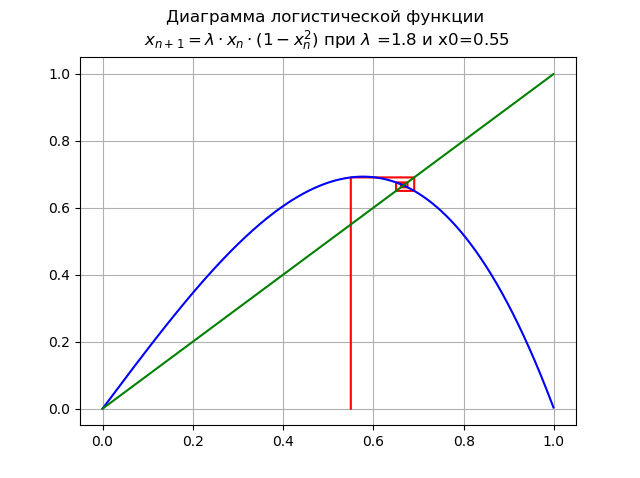
x^{*} = 0

$x ^ {*} = 0$ 安定性を失い、新しい安定点が表示されます

x_{1}^{*}

$x_ {1} ^ {*}$

で

1.99 < l a m b d a <= 2.235 . .

$1.99 <\ lambda <= 2.235 ..$ のために

l a m b d a = $ 2.

$\ lambda = $ 2.$ およびx0 = 0.2：

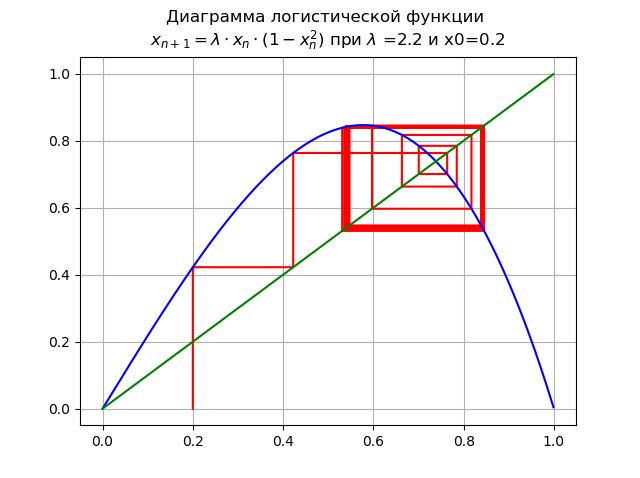
期間の倍増の分岐が発生し、2倍のサイクルが表示されます。さらなる増加

\ラ ム ダ

$\ラムダ$ 周期の倍増分岐のカスケードにつながります。

で

2, 235 < l a m b d a 2.5980 . .

$2,235 <\ lambda 2.5980 ..$ のために

\ラ ム ダ = 2.287

$\ラムダ= 2.287$ およびx0 = 0.2：

増やす

\ラ ム ダ

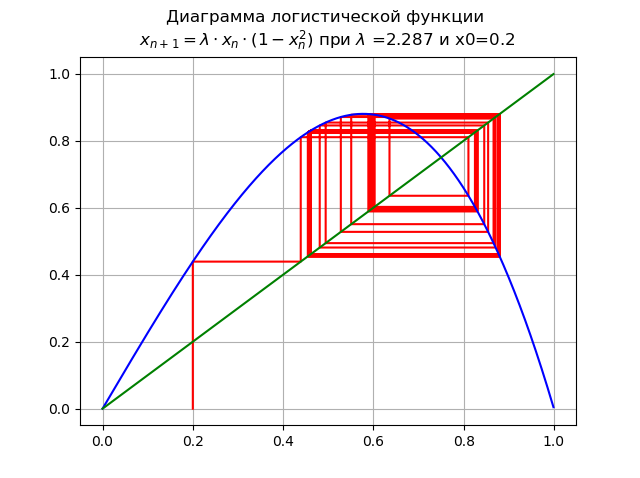
$\ラムダ$ 周期倍増分岐のカスケードにつながりました。

で

\ラ ム ダ = 2.59

$\ラムダ= 2.59$ システムには、考えられるすべての期間の不安定なサイクルがあります。

図に示されているように、ロジスティック関数の次数が増加すると、変化の範囲

$\ラムダ$ テーパー。

図を使用して、値を設定しながら、順序からカオスまでの経路を追跡

\ラ ム ダ

$\ラムダ$ さまざまなロジスティック機能用。カオスを測定する方法は？記事の冒頭にリストされているカオスのタイプのいくつかの答えは知られています

-エントロピーはカオスの尺度です。この答えは、情報カオスに完全に起因する可能性がありますが、ここでどのエントロピーが適用され、すでに考慮されている数値と比較する方法

\ラ ム ダ

$\ラムダ$ -記事の次の部分でこの質問に答えようとします。

情報エントロピーとエントロピー係数

独立したランダムイベントの情報バイナリエントロピーを検討します。

x

$x$ c

n

$n$ 確率とともに分布する可能な状態

p_{i} （ i = 1 、 . . 、 n ）

$p_ {i}（i = 1、..、n）$ 。情報バイナリエントロピーは次の式で計算されます：

H （ x ） = - s u m_{i = 1}^{n} p_{i} c d o t l o g_{2} （ p_{i} ）

$H（x）=-\ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2}（p_ {i}）$

この値は、メッセージの平均エントロピーとも呼ばれます。価値

H_{i} = - l o g_{2} （ p_{i} ）

$H_ {i} =-log_ {2}（p_ {i}）$ i番目の状態のみを特徴付けるプライベートエントロピーと呼ばれます。一般的な場合、エントロピーの定義の対数の底は1より大きくすることができます。彼の選択により、エントロピーの測定単位が決まります。

エントロピーと情報がビット単位で測定される10進数の対数を使用します。たとえば、変数の場合、ビット単位の情報量は正しく計算されます。

X

$X$ そして

\デ ル タ

$\デルタ$ は、エントロピーの対応する式に置換されますが、どの単位でも常に同じ単位になります。確かに：

q = H （ x ） - H （ D e l t a ） = l o g_{10} \左 （ X_{2} - X_{1} \右 ） - l o g_{10} （ 2 D e l t a ） = l o g_{10} （ f r a c X_{2} - X_{1} 2 D e l t a ）

$q = H（x）-H（\ Delta）= log_ {10} \左（X_ {2} -X_ {1} \右）-log_ {10}（2 \ Delta）= log_ {10}（\ frac {X_ {2} -X_ {1}} {2 \ Delta}）$

X

\デ ル タ

$\デルタ$ 同じ単位である必要があります。

実験データからのランダム変数のエントロピー値の推定値は、次の関係からのヒストグラムから見つかります。

D e l t a_{e} = f r a c 12 e^{H （ x ）} = f r a c d 2 p r o d_{i = 1}^{m} （ f r a c n n_{i} ）^{f r a c n_{i} n} = f r a c d n 2 10^{- f r a c 1 n} s u m_{i = 1}^{m} n_{i} l o g_{10} （ n_{i} ）

$\ Delta_ {e} = \ frac {1} {2} e ^ {H（x）} = \ frac {d} {2} \ prod_ {i = 1} ^ {m}（\ frac {n} { n_ {i}}）^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {-\ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10}（n_ {i}）$

ここで：

d

$d$ –ヒストグラムの各列の幅。

m

$m$ -列の数。

n

$n$ -データの総量;

n_{i}

$n_ {i}$ -データ量

i

$i$ その列。

エントロピー係数は、比率から決定されます。

k_{e} = f r a c D e l t a_{e} s i g m a

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

ここで：

\シ グ マ

$\シグマ$ -標準偏差。

カオスの尺度としての情報エントロピー

エントロピー係数を使用して情報カオスの現象を分析するには、まず関数の分岐図を作成します

x_{n + 1} = f （ x_{n} ） = l a m b d a x_{n} （ 1 - x_{n} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ ヒストグラムの構築中に取得された遷移領域の適用：

分岐図

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

取得するもの：

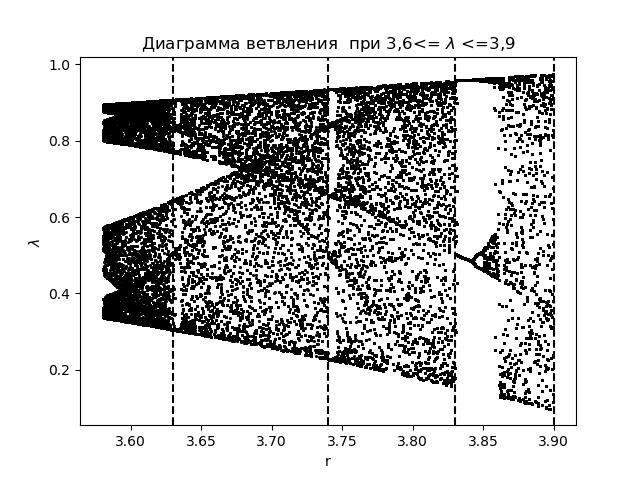
同じ領域のエントロピー係数をプロットします

\ラ ム ダ

$\ラムダ$ ：

エントロピー係数のグラフ

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

取得するもの：

ダイアグラムとグラフを比較すると、ダイアグラム上の領域と、関数のエントロピー係数のグラフ上に同じ領域が表示されています

x_{n + 1} = f （ x_{n} ） = l a m b d a x_{n} （ 1 - x_{n} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ 。

エントロピー係数を使用して情報カオスの現象をさらに分析するために、ロジスティック関数の分岐図を作成します。

x_{n + 1} = f （ x_{n} ） = l a m b d a c d o t x_{n} c d o t （ 1 - x_{n}^{2} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$ 移行領域の適用：

分岐図

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

取得するもの：

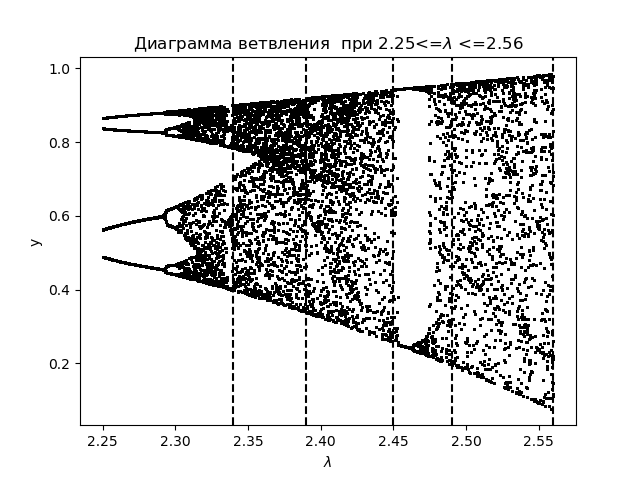
同じ領域のエントロピー係数をプロットします

\ラ ム ダ

$\ラムダ$ ：

エントロピー係数グラフ

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

取得するもの：

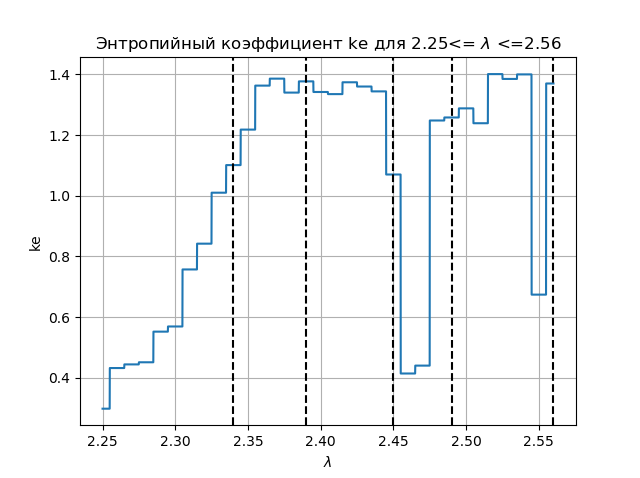
ダイアグラムとグラフを比較すると、ダイアグラム上の領域と、関数のエントロピー係数のグラフ上に同じ領域が表示されています

x_{n + 1} = f （ x_{n} ） = l a m b d a c d o t x_{n} c d o t （ 1 - x_{n}^{2} ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

結論：

教育の問題は記事で解決されています。情報エントロピーはカオスの尺度であり、Pythonの答えはこの質問に対する肯定的な答えを与えます。

カオスの情報エントロピー

はじめに

秩序からカオスへの移行のメカニズム

情報エントロピーとエントロピー係数

カオスの尺度としての情報エントロピー

結論：

参照資料

More articles: