📓 🍦 🍂 電磁波の到来方向を決定するためのMUSICアルゴリズムをモデル化します 😈 🛤️ 👨🏼‍💼

アスキャッツ

まえがき

遠方から紹介を始めます。むかしむかし、2016年から2017年にかけて、あなたの謙な召使は、遠く離れた都市のイルメナウ（ドイツ）に6か月のトレーニングコースを受講し、修士課程の通信と信号処理を無事に完了しました。このプログラムは簡単なものではありませんでしたが、今では思い出すのも楽しいです。時々...

そのため、このトレーニングの最後に、卒業証書に加えて、私はまだかなりの数の異なる資料を手に持っていますが、共有しないのは間違っていると思いました。

これらの資料の1つが目の前にあります。

セミナーの準備中に私が追求した目標 ：

最もアクセスしやすいアンテナアレイのトピックで既に確立されている「スマート」なアプローチについて話し、それをロシア語で行います。
Python 3で小さなシミュレーションを実行して、仲間のラジオエンジニアを動揺させて、プログラミング言語を詳しく調べます（まだ詳しく見ていない場合）。
良い英語の文学へのリンクを提供する-外国の情報源を読まずに、今はどこでもない。

考慮事項 ：

MUSICメソッド（マルチシグナル分類）-これは、実際にはプレビューを指します。

チャート形成とMVDRメソッドの例はここにあります（追加の資料について質問や提案がある場合は、Github.Gistで議論を続けることができます）。

上で言ったように、Pythonを使用します。

import numpy as np import matplotlib.pyplot as plt

線形代数モデリングの最も人気があり便利な候補の1つであるMATLABを試してみませんか？というのも、Pythonで同様の作業を行うことができ、Pythonの範囲はMATLABの範囲よりもはるかに広いためです。したがって、私の意見では、Python構文に精通していると便利です。

さあ始めましょう！

数式はhttps://upmath.me/で作成されます。すばらしいツールを作成してくれたクリエイターに感謝します！

問題の声明

互いに間隔を空けた多数の要素で構成される線形アンテナアレイがあるとします。 $\ Delta = \ frac {\ lambda} {2}$ （アンテナアレイのステップ）、ここで $\ラムダ$ -キャリア電磁（EM）波の長さ。

このアンテナアレイには、さまざまな方向から電磁波が落ちます。

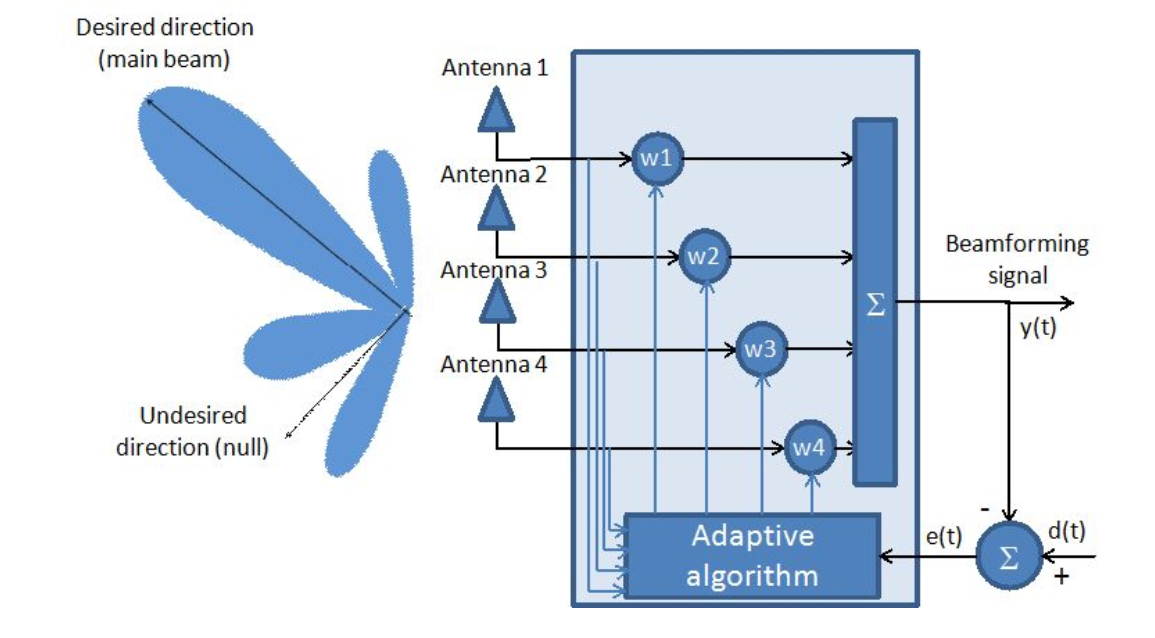
図 1. アダプティブアンテナシステム。

図からわかるように、アンテナアレイは適応フィルターと見なされます。

実際、係数の最適なベクトルを見つける（ $\ mathbf {w} _ {opt}$ ）は、数学的な観点からのアダプティブアンテナアレイの主なタスクです。

最初は、信号がどの方向から来ているのか、何個あるのかはわかりません。この矛盾を解決するために、空間周波数を高解像度で推定するアルゴリズムであるMUSICアルゴリズムを使用します。

受信信号シミュレーション

次の式を使用して、受信信号のモデルを提示できます。

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

どこで $\ mathbf {A} = [\ mathbf {a}（\ theta_1）\ quad \ mathbf {a}（\ theta_2）\ quad ... \ quad \ mathbf {a}（\ theta_d）]$ -アンテナアレイのスキャンベクトル（ステアリングベクトル）の行列（ $a_i = \ exp（-j \ mu m_i）$ 、 m = 0、1 ...（M-1）、 -アンテナアレイの要素数、 -EM波の発生源の数、 $\シータ$ -EM波の到来方向の角度）、 $\ mathbf {S}$ -送信された文字のマトリックス、および $\ mathbf {N}$ -加法性ノイズのマトリックス。

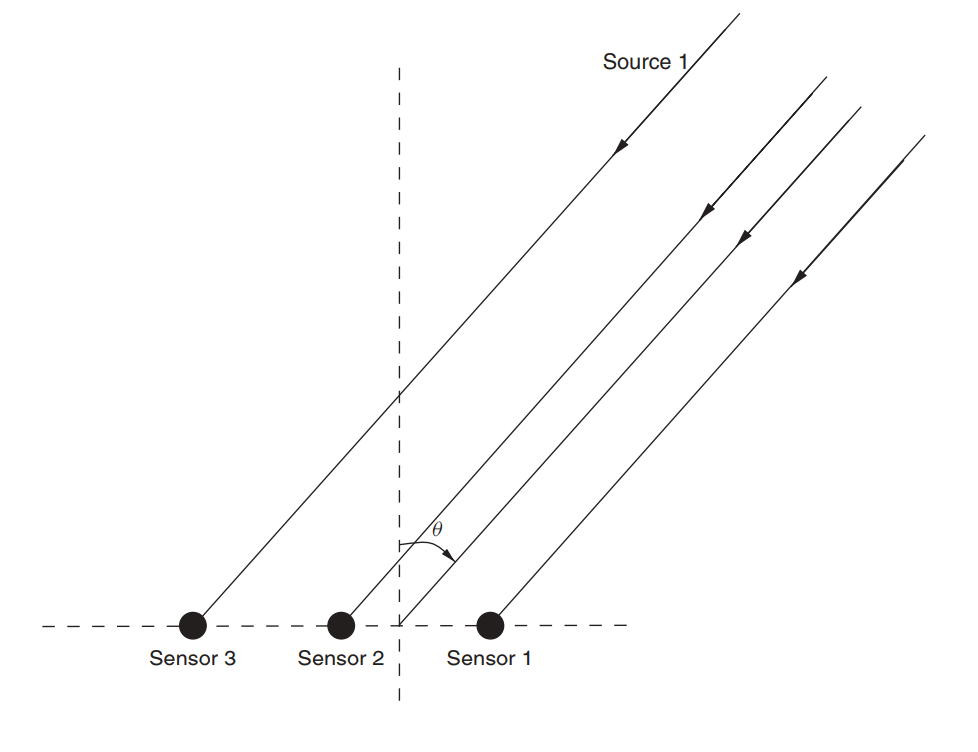
図 2.全方向性線形アンテナアレイ（ULAA-均一線形アンテナアレイ）[1、p。 32]。

この式を「毎日」の方法で再考しましょう。グリッドでは、さまざまな信号からいくつかの「混乱」を取得します。 $\ mathbf {X}$ 。送信元と方向の数に関する情報を明示的に受信することはありませんが、これに関する情報は受信信号に含まれています。

検索を開始しています！

これを行うために、彼らは通常、複雑な信号振幅の行列自体ではなく、共分散（つまり、実際にはべき乗）を使用した操作に進みます：

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

条件

考慮すべき重要な条件を紹介します：レイリー角度分解能の制限：

$sin（\ theta_R）= \ frac {\ lambda} {D}$

どこで $D = M \デルタ$ 線形格子の長さです。

空間周波数の概念により、電磁波の到来角を再定義します。

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin（\ theta_R）= \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

どこで $\ mu_R$ -ビームのメインローブの標準幅（標準ビーム幅）があります。

私たちの方法がどれほど効果的で、どのような条件下であるかを確認するために、角度分離の値をいくつか紹介します：

$\ mu_1 =-\ mu_R、\ quad \ mu_2 = 0、\ quad \ mu_3 = \ mu_R \ quad$ -1つのビーム幅への分割。
$\ mu_1 = -0.5 \ mu_R、\ quad \ mu_2 = 0、\ quad \ mu_3 = 0.5 \ mu_R \ quad$ -1秒のビーム幅への分割。
$\ mu_1 = -0.3 \ mu_R、\ quad \ mu_2 = 0、\ quad \ mu_3 = 0.3 \ mu_R \ quad$ -ビーム幅の3/10に分割。

入力パラメーターを定義します。

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

メソッド自体に関する少しの理論

まず、MUSIC法の先駆者はピサレンコ法（1973）であることに注意してください。ピサレンコ法で考慮される問題は、ホワイトノイズの複素指数の和の周波数を推定することでした。 V.F. Pisarenkoは、自己相関行列の最小固有値に対応する固有ベクトルから周波数を見つけることができることを実証しました。その後、このメソッドはMUSICメソッドの特殊なケースになりました。 [2、p。 459]

シュミットと彼の同僚は、1979年に多重信号分類アルゴリズム（MUSIC）を提案しました[4]。このアルゴリズムの主なアプローチは、受信信号の共分散行列を固有値に分解することです。このアルゴリズムは無相関ノイズを考慮するため、生成される共分散行列は対角形式になります。ここでは、信号およびノイズの部分空間は線形代数を使用して計算され、互いに直交しています。したがって、アルゴリズムは直交性プロパティを使用して、信号およびノイズの部分空間を抽出します[5]。

一般化されたMUSICアルゴリズムは、次のように定義できます。

共分散行列を見つける $\ mathbf {R} _ {xx}$
EVDまたは別の適切な数値アルゴリズムを介して固有ベクトルを見つけます。

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad（1）$

擬似スペクトル（接頭辞pseudoを使用する理由、以下で説明します）MUSICを次の式で見つけます。

$P_ {MU}（e ^ {j \ omega}）= \ frac {1} {\ sum \ limits_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad（2）$

どこで $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega}＆e ^ {j1 \ omega}＆e ^ {j2 \ omega}＆...＆e ^ {j（M-1）\ omega } \ end {bmatrix} ^ T$ 与えられた範囲にある周波数ωの指数ベクトルであり、 $\ mathbf {u} _i$ -行列（1）の雑音部分空間に対応する共分散行列（1）のi番目の固有ベクトル（固有ベクトル）-したがって、 d + 1 （マトリックスのランクです（1））。

より明確にするために、 referenceが提供する適切なMATLABスクリプトを実行してください。 2つの主な点に注意してください。

分母の2番目のノルムの2乗を計算する代わりに（2）、著者はFFTアルゴリズムを固有ベクトルに適用します。これにより、組み込み関数を使用してモデリングが容易になり、一般に、数学的な観点から理論に矛盾しません。
共分散行列は畳み込み行列を通じて計算され、空間周波数を推定するための別のアプローチが上に示されました。

名前から推測できるように、MUSICは受信の方向を高解像度で評価するための古典的な方法でもあります。このコンテキストで擬似スペクトルを計算するためのアルゴリズムを以下に示します。

受信信号の共分散行列を見つけます。
ゼロ部分空間を見つける $\ mathbf {U} _0$ ：

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

検索範囲を選択します。

$a（\ mu）= \ begin {bmatrix} e ^ {j0 \ mu_1}＆...＆e ^ {j0 \ mu_Q} \\ ...＆...＆... \\ e ^ {j（ M-1）\ mu_1}＆...＆e ^ {j（M-1）\ mu_Q} \ end {bmatrix}$

どこで $\ mu =-\ frac {2 \ pi f_c} {c} \ Delta sin \ theta =-\ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

擬似スペクトルを計算する：

$P_ {MU}（\ theta）= \ frac {\ mathbf {a} ^ H（\ theta）\ mathbf {a}（\ theta）} {\ mathbf {a} ^ H（\ theta）\ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a}（\ theta）}$

スペクトル分析とEM波の到来角分析（DoA-到来方向）の関係を表1に示します。

表1 MUSICアプリケーション間の通信 ：信号配列処理と高調波検索[6]。

可変	信号配列処理	調和検索
	センサー数	期間の数
	期間の数	実験の数
	波面の数	複雑なコンポーネントの数
$\ mu$	空間周波数	正規化された周波数

一般に、配列（格子）を介して受信するプロセスは、古典的な離散化のプロセスと比較できます。実際、特定の位相遅延（つまり、特定の時間遅延）のある波を受信する各センサーは、サンプリングデルタパルスの機能を実行します。古典的なスペクトル分析の実現（実験）の数は、時間セグメント（スナップショット）の数に対応します。各ソースには独自の波面があり、これはスペクトル解析の場合の信号の一意の正弦波の数に相当します。

そして、固有ベクトルを計算する瞬間に戻りましょう。上記のベクトル $a（\ theta_i）\イプシロンA$ どこで i = 1,2、..、d 共分散行列のノイズ部分空間に直交する、すなわち：

$a（\ theta_i）^ TU_0 = 0 ^ T$

実際には、方程式系があり、それを解くことで根-固有ベクトルを見つけることができます。このような方法は、数値アルゴリズム（前述のようにEVDに適用される）とは対照的に、近似固有値ではなく実固有値を取得できます。そのため、このアプローチでは、擬似スペクトルではなくスペクトルを取得できます。同じ考えがルートMUSICアルゴリズムの基礎を形成しました。

モデリング

ふふ！最後に、すべての式について説明し、ある程度説明します。モデリングを開始できます。

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

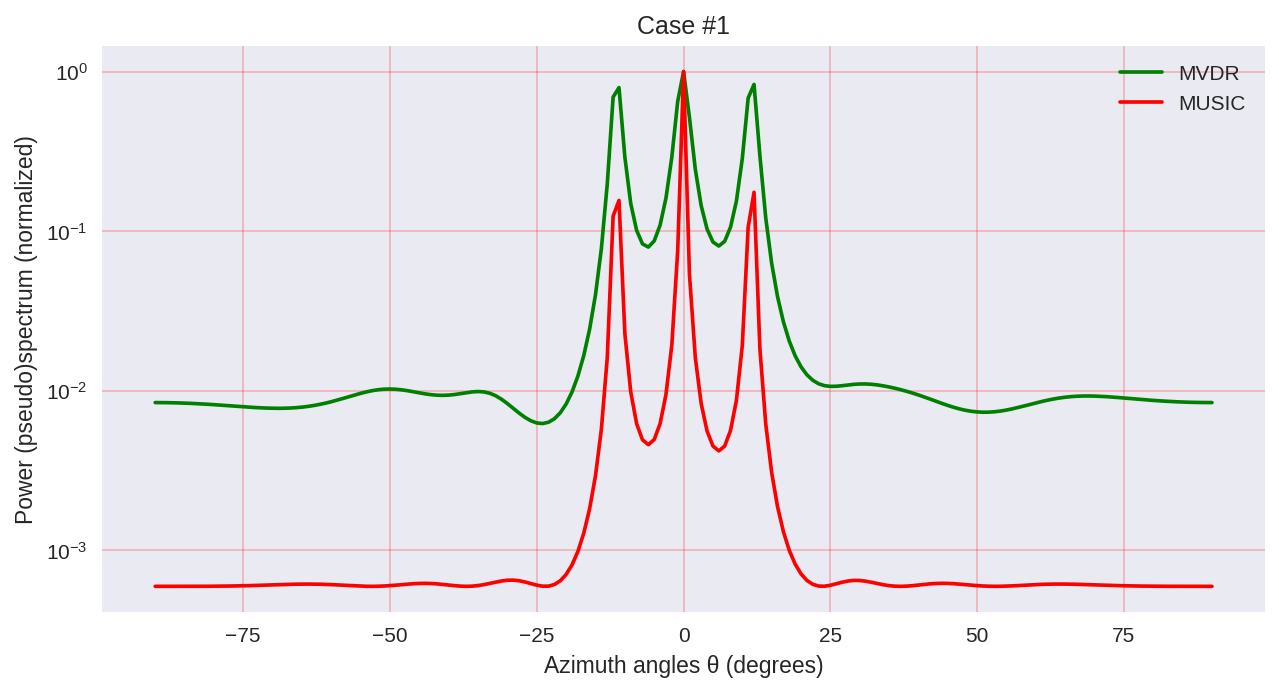
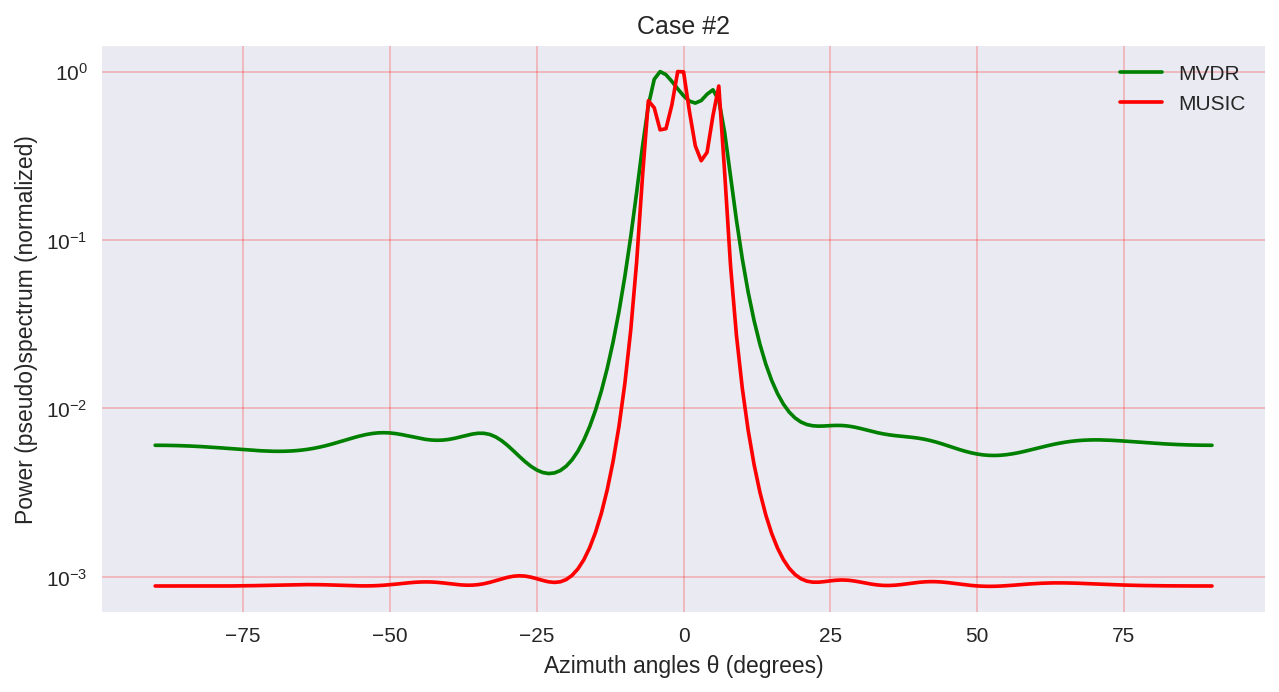
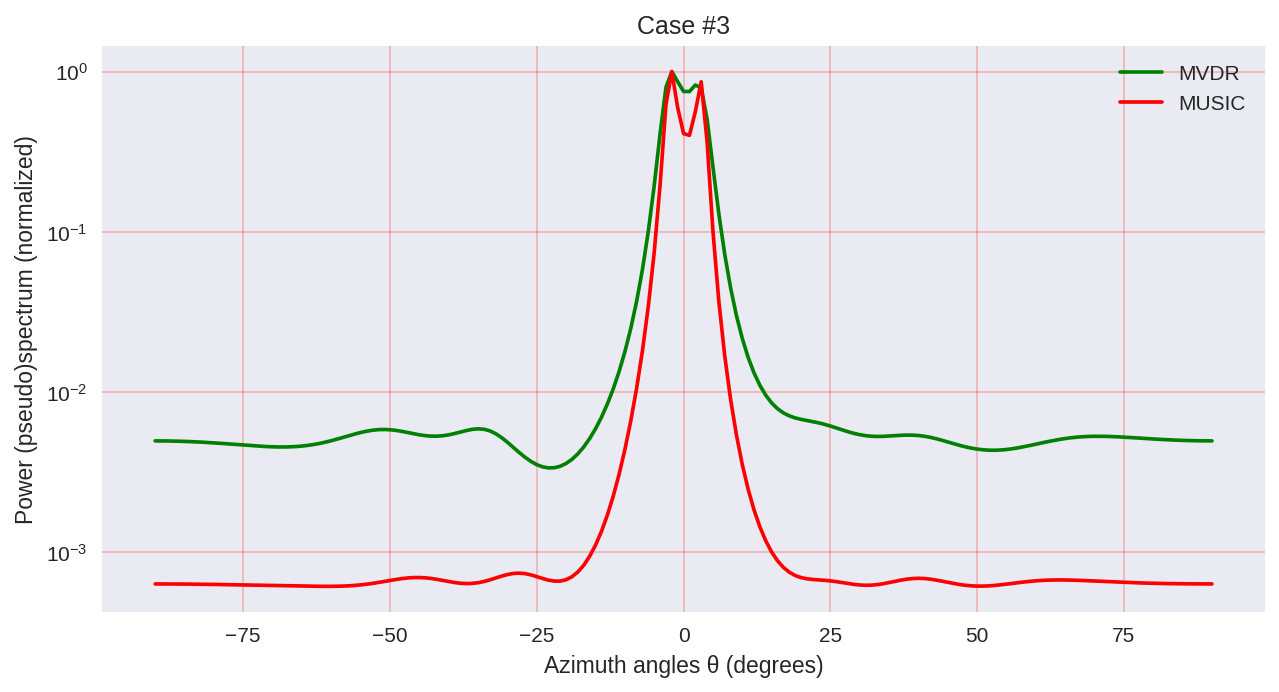
ご覧のとおり、MUSICの方が解像度が高く、一般に、たとえばMVDRの場合よりも優れた結果を得ることができます-スペクトル分析のパラメトリック手法の代表例です。

ただし、MUSICを使用する場合、EVDやSVDなどの計算コストの高いアルゴリズムを使用することに注意してください。

そのようなこと。

使用された文献のリスト：

ヘイキン、サイモン、KJレイリュー。アレイ処理およびセンサーネットワークに関するハンドブック。巻 63.ジョンワイリー＆サンズ、2010年。 102-107
Hayes MH統計デジタル信号処理およびモデリング。 -ジョンワイリー＆サンズ、2009年。
Haykin、Simon S.適応フィルター理論。 Pearson Education India、2008。pp。 422-427
Richmond、Chris D.「Caponアルゴリズムの平均二乗誤差しきい値SNR予測と解像度の確率。」 IEEE Transactions on Signal Processing 53.8（2005）：2748-2764。
SKP Gupta、MUSIC、および改良されたMUSICアルゴリズムにより、到着の方向付けをシミュレートします（IEEE、2015年）。
マーティン・ハート教授の講義（ array array ）

電磁波の到来方向を決定するためのMUSICアルゴリズムをモデル化します