スイープライン法によるドロネー三角形分割アルゴリズム

良い一日！



この記事では、「直線を掃く」というアイデアを使用して平面上にドロネー三角形分割を作成した結果として得られたアルゴリズムについて詳しく説明します。 三角測量に関する記事を読んだときに出会ったことのないアイデアがいくつかあります。

おそらく誰かがそれらを珍しいと思うでしょう。 私は最善の伝統ですべてを行い、次のことをストーリーに含めます：使用されるデータ構造の説明、アルゴリズムのステップの説明、正確性の証明、時間推定、およびkDツリーを使用した反復アルゴリズムとの比較。

問題の定義と説明

三角測量

いくつかのポイントのペアがエッジで接続されている場合、平面上のポイントのセットに三角形分割が与えられ、結果のグラフの有限面は三角形を形成し、エッジは交差せず、グラフはエッジの数が最大になると言われています。

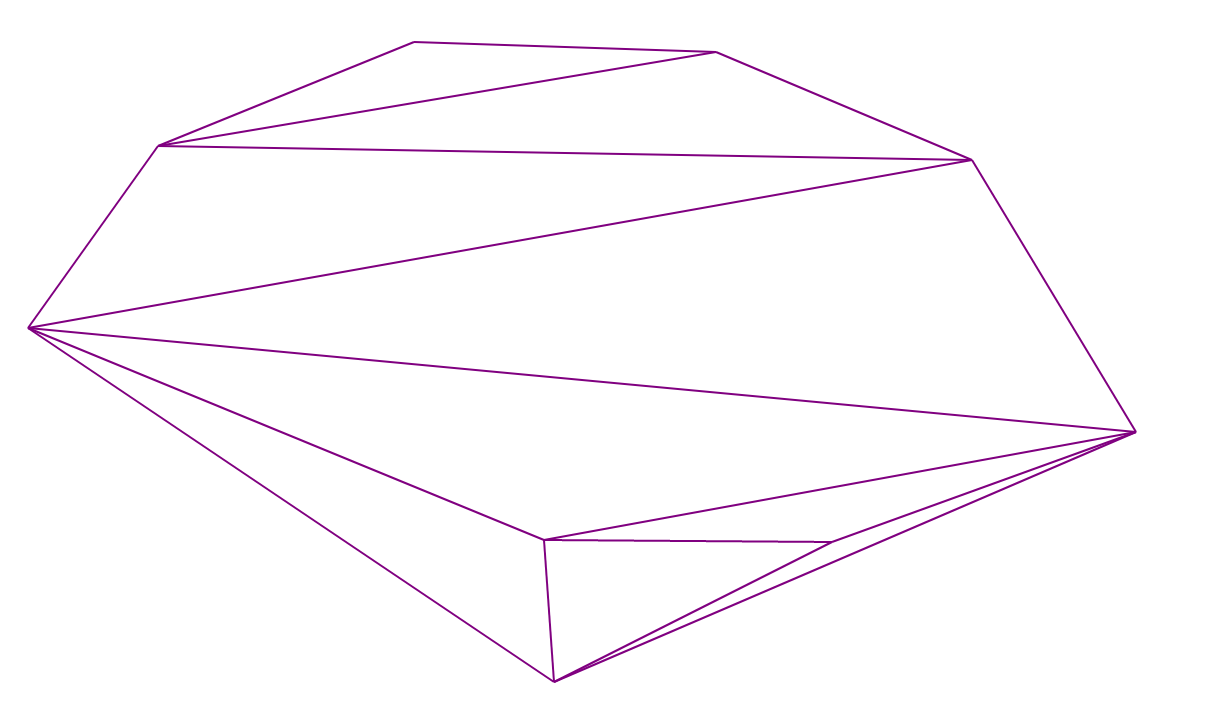
ドローネ三角形分割

Delaunay三角形分割は、三角形の周囲に外接する円の内側に元のセットの点が存在しないことが事実であるような三角形分割です。

注 ：同じ円上に4つのポイントがない特定のポイントセットの場合、ドロネー三角形分割は1つだけです。

ドローネ条件

点の集合に三角形分割を与えます。 このサブセットに囲まれた三角形分割が彼のドロネー三角形分割である場合、ポイントの特定のサブセットはドロネー条件を満たしていると言います。

ドローネ三角形分割の基準

三角形分割で四角形を形成するすべての点でドロネー条件が満たされることは、この三角形分割がドロネー三角形分割であるという事実と同等です。



注 ：非凸四角形の場合、ドローネ条件は常に満たされ、凸四角形（頂点が同じ円上にない）の場合、正確に2つの三角形分割が可能です（そのうちの1つはドロネー三角形分割です）。

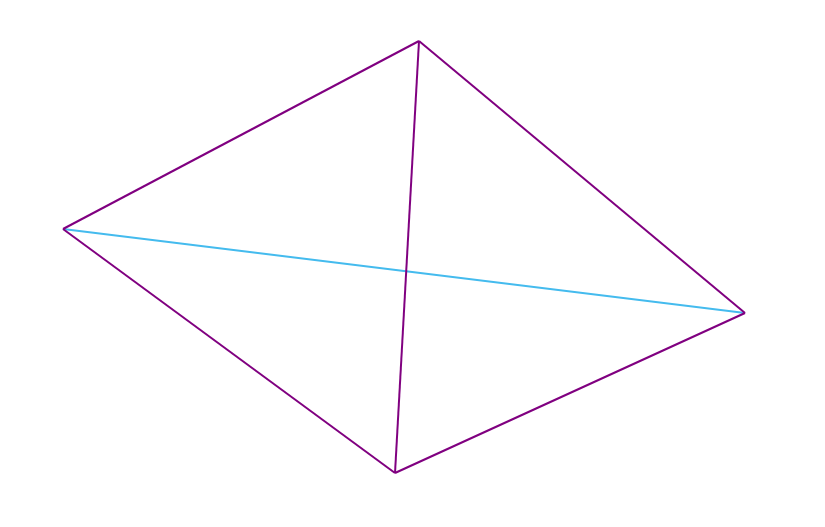
タスクは、与えられたポイントのセットに対してドロネー三角形分割を作成することです。

アルゴリズムの説明

可視点と可視エッジ

点の有限集合（集合のすべての点を含む多角形を形成するようにいくつかの点を接続するエッジ）と、ハルの外側にある点Aの最小凸包（以下、MBO）を与えます。 平面のポイントがポイントAに接続されているセグメントがMBOと交差していない場合、ポイントはポイントAに対して可視と呼ばれます。



MBOエッジは、Aの両端が見える場合、ポイントAで可視と呼ばれます。



次の画像では、赤い点に見える端が赤でマークされています。

注 ：Delaunay三角形分割の輪郭は、それが構築されるポイントのMBOです。



注2 ：アルゴリズムでは、追加されたポイントAに表示されるエッジはチェーンを形成します。つまり、複数のMBOエッジが連続しています。

三角測量をメモリに保存する

Skvortsovの本[1]で詳しく説明されている標準的な方法がいくつかあります。 アルゴリズムの仕様により、独自のバージョンを提供します。 Delaunay条件の4ゴンをチェックするため、それらの構造を考慮します。 三角形分割の各四角形は、共通のエッジを持つ2つの三角形です。 各エッジには、ちょうど2つの三角形が隣接しています。 したがって、三角形分割の各四角形は、エッジと、隣接する三角形のエッジの反対側にある2つの頂点によって生成されます。

2つの三角形とその隣接関係がエッジと2つの頂点に沿って復元されるため、このような構造すべての三角形分割を復元できます。 したがって、セットに2つの頂点を持つエッジを格納し、エッジ（頂点の順序付けられたペア）に沿って検索を実行することが提案されています。

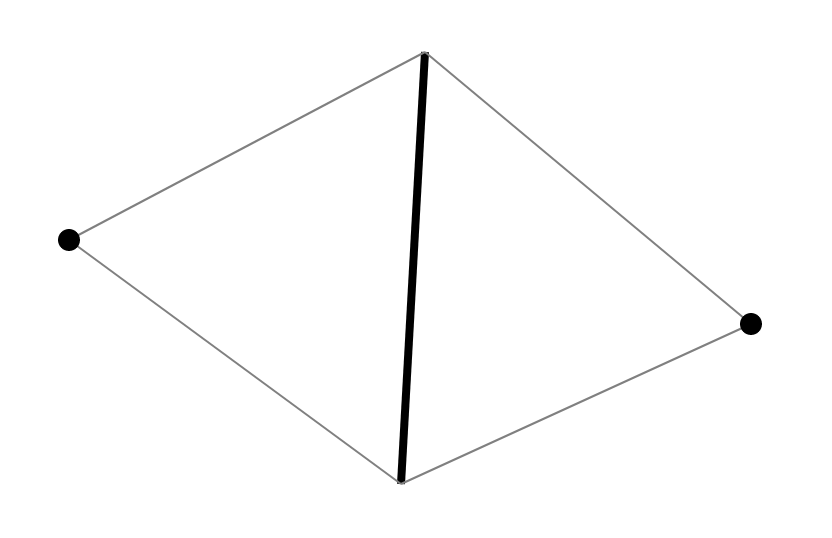
アルゴリズム

スイープラインのアイデアは、すべてのポイントが一方向にソートされ、順番に処理されることです。

1. すべてのポイントを直線に沿って並べ替えます（簡単にするため、座標で $$$x$ ）
2. 最初の3点に三角形を作成します。
   
   
   
   さらに、次の各ポイントに対して、既に追加されているポイントのDelaunay三角形分割、およびそれらのMBOが存在するという不変条件を保存する手順を実行します。
3. 可視エッジとポイント自体によって形成された三角形を追加します（つまり、問題のポイントから可視エッジのすべての端にエッジを追加します）。
4. 可視エッジによって生成されたすべての四角形をドローネ条件で確認します。 どこかで条件が満たされない場合、四角形の三角形分割を再構築し（2つしかないことを思い出します）、現在の四角形のエッジによって生成された四角形のチェックを再帰的に実行します（ドローネ条件に違反した後のみ）。

注 ：再帰的開始時のステップ（4）では、この反復で考慮されるポイントから来るエッジによって生成される四角形をチェックできません（常に4つのうち2つがあります）。 ほとんどの場合、凸ではないため、証明は純粋に幾何学的であるため、読者に任せます。 さらに、リビルドごとに2回だけ再帰的な開始が実行されると想定しています。

ドローネ状態の検証

ドローネ条件の四角形をテストする方法は、同じ本[1]に記載されています。 そこから三角関数を持つメソッドを選択すると、不正確な実装でサインの負の値が取得される可能性があり、モジュロを取るのが理にかなっています。

目に見えるエッジを検索する

目に見えるエッジを効果的に見つける方法を理解することは残っています。 以前に追加されたポイントSは最大の座標を持つため、現在の反復ではMBOにあることに注意してください。 $$$x$ 、現在のポイントでも表示されます。 次に、可視エッジの端が可視ポイントの連続チェーンを形成することに注意して、MBOに沿って両方向にポイントSから移動し、可視の間にエッジを収集します（エッジの可視性はベクトル積を使用してチェックされます）。 したがって、MBOを二重接続リストとして保存すると便利です。各反復で、目に見えるエッジを削除し、問題のポイントから2つの新しいエッジを追加します。

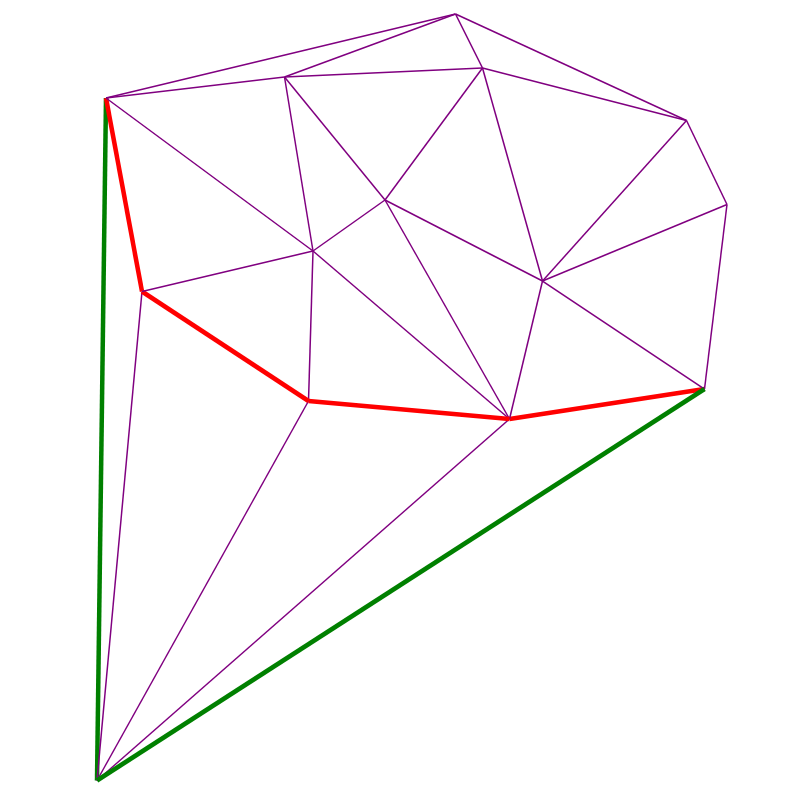
アルゴリズムの視覚化

2つの赤い点-追加および前。 各瞬間の赤いエッジは、ステップ（4）からの再帰スタックを構成します。

アルゴリズムの正確さ

アルゴリズムの正しさを証明するには、ステップ（3）および（4）で不変量の保存を証明するだけで十分です。

ステップ（3）

ステップ（3）の後、明らかに、現在のポイントセットの三角形分割が得られます。

ステップ（4）

ステップ（4）のプロセスでは、ドローネ条件を満たさないすべての四角形が再帰スタックにあります（説明を参照）。これは、ステップ（4）の終わりに、すべての四角形がドローネ条件を満たしていることを意味します。つまり、ドローネ三角形分割が実際に構築されます。 その後、ステップ（4）のプロセスがいつか終了することを証明する必要があります。 これは、再構築中に追加されたすべてのエッジが問題の現在の頂点から来るという事実に基づいています（つまり、ステップ $$$k$ しかありません $$$k-1$ ）そして、これらのエッジを追加した後、それらによって生成された四角形を考慮しないという事実から（前のコメントを参照）、つまり、追加するのは1回のみです。

時間の複雑さ

平均して、アルゴリズムは均一な正規分布で非常にうまく機能します（結果を以下の表に示します）。 その作業時間は $$$O（NlogN）$ 。 最悪の場合、評価が行われます $$$O（N ^ 2）$ 。

作業時間を部分的に見て、どれが総時間に最も大きな影響を与えているかを理解しましょう。

方向で並べ替え

ソートには、推定値を使用します $$$O（NlogN）$ 。

目に見えるエッジを検索する

まず、可視エッジの検索に費やした合計時間が $$$O（N）$ 。 各反復で、線形時間ですべての可視エッジとさらに2つ（最初の非可視）が見つかることに注意してください。 ステップ（3）では、MBOに新しい2つのエッジを追加します。 したがって、合計で、 $$$2N$ rib骨、したがって、さまざまな目に見えるrib骨はもはやなくなります $$$2N$ 。 私たちも見つけます $$$2N$ 見えないエッジ。 したがって、合計でこれ以上はありません $$$4N$ 時間に対応するrib骨 $$$O（N）$ 。

新しい三角形の構築

ステップ（3）から三角形が構築され、可視エッジが既に見つかっている合計時間は明らかに $$$O（N）$ 。

三角測量の再構築

手順（4）の処理は残ります。 まず、ドローネの条件を確認し、満たされていない場合は再構築することは非常に費用のかかるアクションです（ただし、 $$$O（1）$ ） Delaunay条件を確認する場合のみ、約28の算術演算を実行できます。 このステップでの再構築の平均回数を見てみましょう。 一部の分布の実際の結果を以下に示します。 彼らにとって、再配置の平均数は対数速度で増加すると本当に言いたいのですが、これを仮定のままにしておきましょう。

ここで、ポイントごとの再配置の平均数は、並べ替えが実行される方向によって大きく異なる可能性があることにも注意してください。 したがって、アスペクト比が100000：1の長い低い長方形に均等に分散された100万の場合、この数は1.2から24に変化します（これらの値は、データをそれぞれ水平および垂直にソートするときに達成されます）。 したがって、任意の方法でソート方向を選択する（この例では、平均で約2回の再構築が行われた）か、データが事前にわかっている場合は手動で選択することに注意してください。



したがって、プログラムが通常ステップ（4）に要する時間。 実行速度が速い場合、ソートの高速化を検討するのは理にかなっています。

最悪の場合

最悪の場合 $$$k$ 番目の反復が発生します $$$k-1$ ステップ（4）の再帰呼び出し、つまりすべてのiを合計すると、最悪の場合の漸近的な動作が得られます $$$O（N ^ 2）$ 。 次の図は、プログラムが長時間動作できる美しい例を示しています（10,000ポイントの入力で新しいポイントを追加すると、平均で1100が再構築されます）。

kDツリーを使用してDelaunay三角形分割を構築するための反復アルゴリズムとの比較

反復アルゴリズムの説明

上記のアルゴリズムについて簡単に説明します。 次のポイントが到着すると、kDツリーを使用します（分からない場合は、どこかで読むことをお勧めします）。すでに非常に近い三角形を見つけます。 次に、深さをバイパスして、ポイント自体が入る三角形を探します。 見つかった三角形の頂点までエッジを拡張し、新しい四角形のアルゴリズムから実際にステップ（4）を実行します。 ポイントは三角形分割の外側にある可能性があるため、簡略化のために、すべてのポイントを大きな三角形で覆うこと（事前に構築すること）を提案します。これにより問題が解決します。

アルゴリズムの類似性

実際、方向によってソートされた順序でポイントが追加される場合、再配置の数が少ないことを除いて、アルゴリズムは実際には反復と同じように機能します。 次のアニメーションはこれを非常によく示しています。 その上で、ポイントは右から左に追加され、それらはすべて大きな三角形で覆われ、その後削除されます。

アルゴリズムの違い

反復アルゴリズムでは、ポイントの定位（目的の三角形の検索）は平均して $$$O（logN）$ 、上記の分布では、ポイントの供給の任意の順序の条件下で、平均して、3つの再配置が発生します（[1]を参照）。 したがって、スイープラインは、ローカリゼーションで反復アルゴリズムの時間を獲得しますが、再構築ではそれを失います（これは非常に難しいことです）。 さらに、反復アルゴリズムはオンラインでも機能しますが、これもその特徴的な機能です。

おわりに

ここでは、アルゴリズムの操作から生じるいくつかの興味深い三角形分割を示します。

美しい模様

正規分布、1000ポイント

均一な分布、1000ポイント

ロシアのすべての都市の場所に基づいた三角測量

ここで、このアルゴリズムの私のコードの例を見ることができます：

github.com/Vemmy124/Delaunay-Triangulation-Algorithm



ご清聴ありがとうございました！

文学

[1] Skvortsov A.V. ドローネの三角形分割とその応用。 -トムスク：出版社トム。 大学、2002年-128秒 ISBN 5-7511-1501-5