エラーが罪に変わる方法

ある都会の伝説によると、消費者はコップの半分に割らず、先端をそっとはがすことを知ったとき、砂糖袋、スティックの作成者は首を吊った。 もちろん、これはそうではありませんが、この論理に従うと、 ウィリアム・ゴセットという名前のイギリスのギネスビール愛好家は、自分自身を掛けるだけでなく、coの中で彼の回転で地球をまさに中心に掘削するはずです。 そして、すべては、 学生の仮名の下で公開された彼の象徴的な発明が何十年も悲惨なほど誤用されているためです。

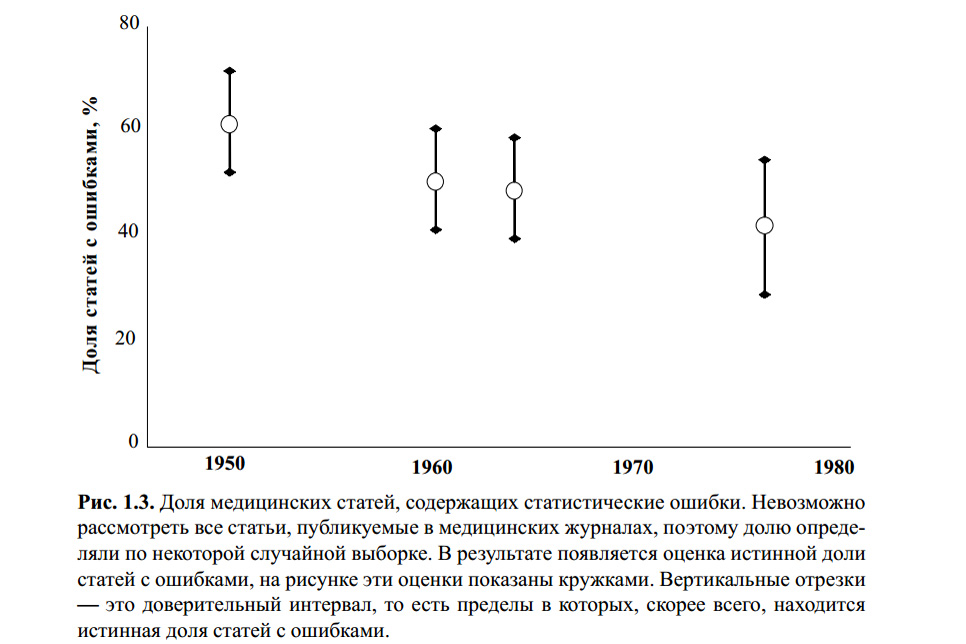
上の図は、 S。グランツの本からのものです。 生物医学統計。 あたり 英語から -M.、Practice、1998年-459 p。 統計エラーについてこのチャートの統計を確認した人がいるかどうかはわかりません。 しかし、このトピックに関する多くの最新記事と私自身の経験から、スチューデントのt基準は依然として最も有名であり、したがって、使用の有無にかかわらず、最も人気があります。

これの理由は、表面教育（厳密な教師は「統計をチェックする」、そうでなければuuuuuu！が必要だと教えている）、使いやすさ（テーブルとオンライン計算機が豊富に用意されている）、そして「そしてそれが機能する」という事実を掘り下げることへの不本意です。 この基準をコースで少なくとも1回使用した人や科学的な研究でさえ、ほとんどの人は次のようなことを言うでしょう。「さて、攻撃性に関して5人の怒っている学童と7人の学童ゲーマーを比較すると、表の値はp = 0.05そして、これはゲームが悪であることを意味します。ええ、はい、正確にではなく、95％の確率で。 論理的および方法論的な間違いを何回犯しましたか？

基本

スチューデントのt検定は何に基づいていますか？ 論理はベイズの定理から取られ、数学的基礎はガウス分布から取られ、方法論は分散分析に基づいています。

ここで、パラメーターμは分布の数学的期待値（平均値）、パラメーターσは分布の標準偏差（σ²は分散）です。

分散分析とは何ですか？ 特定の年齢の各人の数でソートされたHabrオーディエンスを想像してください。 年齢別の人数は正規分布に従う可能性が高い-ガウス関数によると：

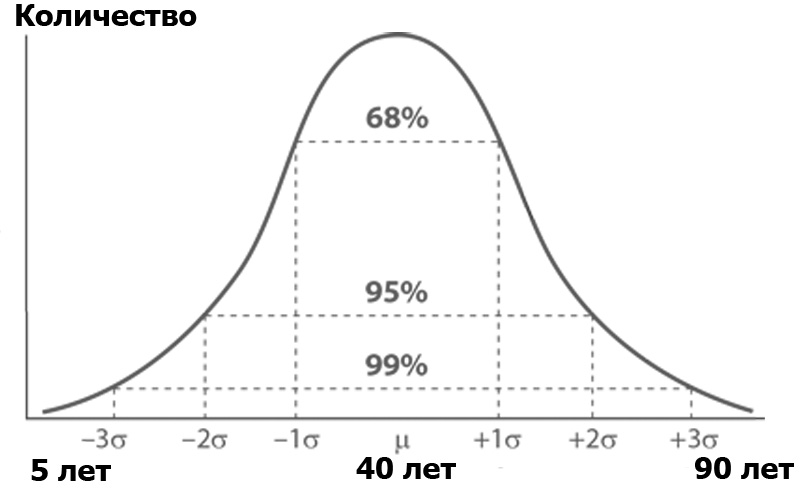
正規分布には興味深い特性があります-その値のほとんどすべては、平均値からの3つの標準偏差の限界にあります。 そして、標準偏差とは何ですか？ これが分散のルートです。 分散は、母集団のすべてのメンバーの差の平方の合計と、これらのメンバーの数で割った平均値です。

$$

$$σ_{n} ^ {2} = {\ frac {1} {n}} \ sum \ limits _ {{i = 1}} ^ {n} \ left（X_ {i}-{\ bar {X} } \右）^ {2}$$

つまり、各値は平均から差し引かれ、マイナスを殺すために二乗されてから、平均を取り、愚かに合計され、これらの値の数で割られました。 結果は、平均-分散に対する値の平均分散の尺度です。

この一般集団で、Cryptocurrencyハブの読者とOld Ironハブの読者の2つのサンプルを選択したとします。 ランダムサンプリングを行うことで、常に正規分布に近い分布が得られます 。 そして今、私たちは人口の中に小さなディストリビューターを獲得しました：

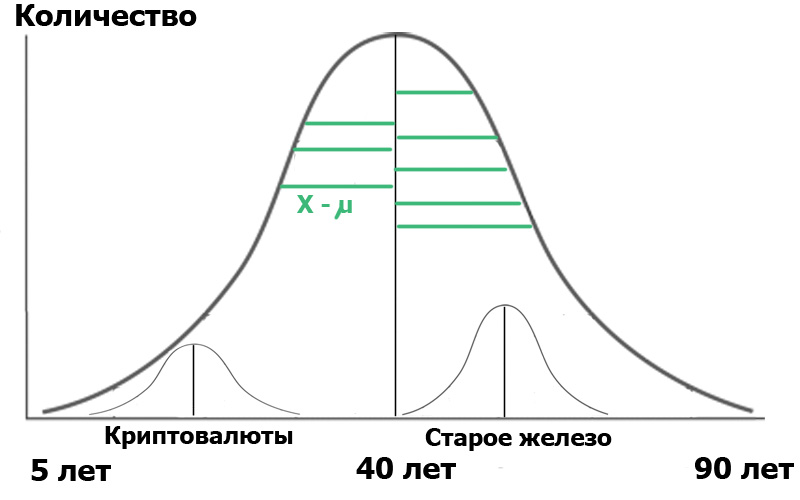
わかりやすくするために、緑のセグメント（分布点から平均値までの距離）を示しました。 これらの緑のセグメントの長さが二乗され、合計され、平均された場合、これが分散になります。

そして今-注目。 これらの2つの小さなサンプルを通じて母集団を特徴付けることができます。 一方では、サンプルの分散は母集団全体の分散を特徴づけます。 一方、サンプル自体の平均値も分散を計算できる数値です！ したがって、サンプルの分散の平均とサンプルの平均値の分散があります。

次に、分散の分析を行い、大まかに論理式の形式でそれを表します。

$$

$$F = {\ frac {分散\：集団\：によって\：平均\：値\：サンプル} {分散\：集団\：によって\：分散\：サンプル}}$$

上記の式から何が得られますか？ とても簡単です。 統計では、すべては「帰無仮説」から始まります。これは、「私たちに思われた」、「すべての偶然はランダム」、つまり「厳密に言えば、観測された2つのイベント間に関係はありません」と定式化できます。 したがって、この場合、帰無仮説は、2つのハブのユーザーの年齢分布に有意差がないことです。 帰無仮説の場合、図は次のようになります。

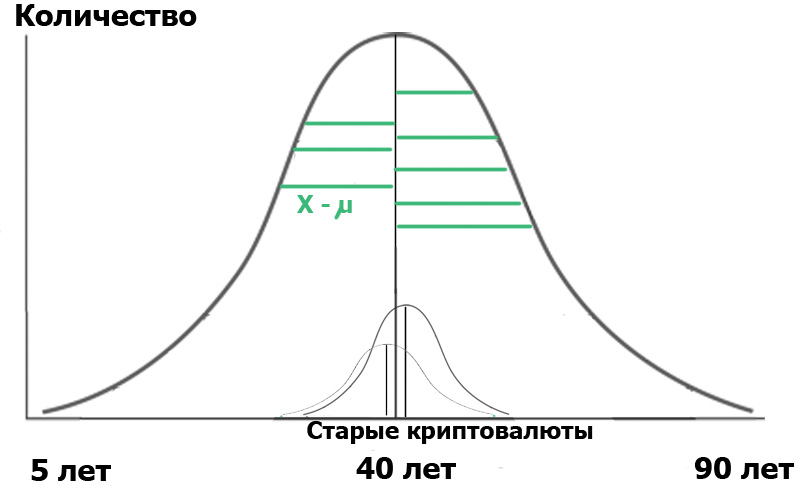
これは、サンプルの分散とその平均値の両方が互いに非常に近いか等しいことを意味するため、非常に一般的に言えば、基準

$$

$$F = {\ frac {分散\：集団\：によって\：平均\：値\：サンプル} {分散\：集団\：によって\：分散\：サンプル}} = 1$$

しかし、サンプルの分散が等しいが、habrausersの年齢が実際に非常に異なる場合、分子（平均値の分散）は大きくなり、Fは1よりもはるかに大きくなります。 ダイアグラムは前の図のようになります。 そして、それは私たちに何を与えますか？ 言葉遣いに注意を払わなければ、何もありません。帰無仮説は有意差がないことです。

しかし、重要なことは...私たちが自分で設定したことです。 これはαとして示され、次の意味があります。 有意水準は、帰無仮説を誤って拒否する最大許容確率です。 つまり、エラーの確率Pがαより小さい場合にのみ、イベントをあるグループと別のグループとの間の有意差と見なします。 これは悪名高いp <0.05です。これは、通常、生物医学研究では有意水準が5％に設定されているためです。

それでは、すべてが簡単です。 αに応じて、Fの臨界値があり、それから帰無仮説を棄却します。 それらはテーブルの形で発行され、私たちはこれを使用することに慣れています。 これは分散分析用です。 そして、学生はどうですか？

だから学生は言った

そして、学生の基準は、分散分析の特別なケースです。 繰り返しになりますが、Googleで簡単に作成できる数式を使用しすぎることはありませんが、その本質を伝えます。

$$

$$t = {\ frac {差\：平均\：値\：サンプル} {標準\：エラー\：差\：サンプル\：平均}}$$

したがって、この長い説明はすべて非常に失礼で流である必要がありましたが、t基準が何に基づいているのかを明確に示しています。 それに応じて、その固有の特性から、その使用の制限に直接従うため、プロの科学者でさえしばしばミスを犯します。

プロパティ1：分布の正規性。

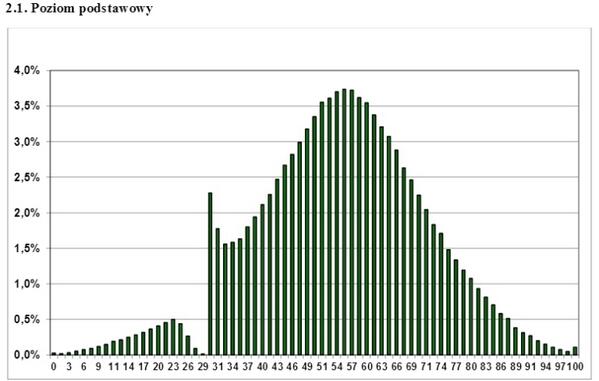
これは、インターネット上のポーランドの国家試験のスコアの分布のグラフとして数年です。 それからどのような結論を引き出すことができますか？ この試験に合格したのは、Gopnikを完全に撃退しただけですか？ どの教師が生徒に「リーチ」しますか？ いいえ、1つのみ-正規分布以外の分布には、Studentなどのパラメトリック分析基準を適用できません。 片側の鋸歯状の波状の離散分布図がある場合は、t基準を忘れて使用することはできません。 ただし、これは深刻な科学的研究によっても無視されることがあります。

この場合の対処方法 いわゆるノンパラメトリック分析基準を使用します。 それらは異なるアプローチ、すなわちデータのランキング、つまり各ポイントの値から割り当てられたランクへの移動を実装します。 これらの基準はパラメトリック基準よりも精度が低くなりますが、異常な母集団に対するパラメトリック基準の不当な使用とは対照的に、少なくともそれらの使用は正しいです。 これらの基準のうち、Mann-WhitneyのU基準は最もよく知られており、「少量のサンプル用」の基準としてよく使用されます。 はい、最大5ポイントのサンプルを扱うことができますが、これはすでに明らかなように、その主な目的ではありません。

2番目のプロパティ：数式を覚えていますか？ F基準の値は、サンプルの平均値の差（分散の増加）によって変化しました 。 ただし、分母、つまり分散自体は変更すべきではありません。 したがって、適用可能性の別の基準は、分散の等価性である必要があります。 このチェックがより頻繁に行われないことは、たとえば、 生物医学データの統計的分析におけるエラーです。 レオノフV.P. International Journal of Medical Practice、2007、no。 2、pp。19-35 。

プロパティ3：2つのサンプルの比較。 彼らは、t基準を使用して3つ以上のグループを比較することを好みます。 原則として、これは次のように行われます：グループAからB、BからC、およびAからC.のペアがペアで比較されます。 この場合、多重比較の効果が生じます。

3つの比較のいずれかでtの十分に高い値を取得した後、研究者は「P <0.05」と報告しています。 しかし実際には、エラーの可能性は5％を大きく超えています。

なんで？

私たちは理解しています：研究では、5％の有意水準が採用されたと仮定します。 これは、グループAとグループBを比較するときに帰無仮説を誤って拒否する最大許容確率が5％であることを意味します。 すべてが正しいように思えますか？ ただし、グループBとCを比較する場合と、グループAとCを比較する場合も、まったく同じ間違いが発生します。 その結果、この種の評価で全体として間違いが発生する確率は5％ではなく、はるかに高くなります。 一般に、この確率は

P ′= 1-（1-0.05）^ k

ここで、kは比較の数です。

そして、我々の研究では、帰無仮説を棄却する際に間違いを犯す確率は約15％です。 4つのグループを比較する場合、ペアの数、したがって、可能なペアワイズ比較は6です。したがって、各比較の有意水準は0.05です。

少なくとも1つの違いを誤って検出する確率は0.05ではなく、0.31です。

それでも、このエラーをなくすことは難しくありません。 1つの方法は、ボンフェローニ改正を導入することです。 ボンフェローニの不等式は、基準をk回適用すると

有意水準がαの場合、少なくとも1つのケースでは、存在しない差を見つける確率は、kとαの積を超えません。 ここから：

α ′<αk、

ここで、α ′は、少なくとも一度は違いを間違える確率です。 次に、問題を非常に簡単に解決します。有意水準をボンフェローニ補正で、つまり比較の多重度で割る必要があります。 3つの比較のために、t検定の表からα= 0.05 / 3 = 0.0167に対応する値を取得する必要があります。 繰り返しますが、非常に簡単ですが、この修正は無視できません。 ちなみに、この修正に夢中になるべきではありません。8で割った後でも、t基準の値は不必要に厳密です。

次に来るのは、ほとんど気付かない「ささいなこと」です。 ここでは、テキストの読みやすさを低下させないために、ここでは数式を意図的に提供していませんが、t基準の計算は以下の場合に異なることに注意してください。

• 2つのサンプルのサイズが異なる（一般に、一般的な場合、2サンプルの基準の式を使用して2つのグループを比較することに注意してください）;

  
  
  
  
  
  
  

• 依存サンプルの可用性。 これらは、異なる時間間隔で1人の患者からデータが測定される場合、実験前後の動物のグループからのデータなどです。

  
  
  
  
  
  
  

最後に、何が起こっているかを完全に想像できるように、t基準の誤った使用に関する最新のデータを提供します。 数は、多くの中国の科学雑誌の1998年と2008年のものであり、彼らは自分自身で語っています。 私は、これが不正確な科学データよりも不正確な設計になることを本当に望んでいます：

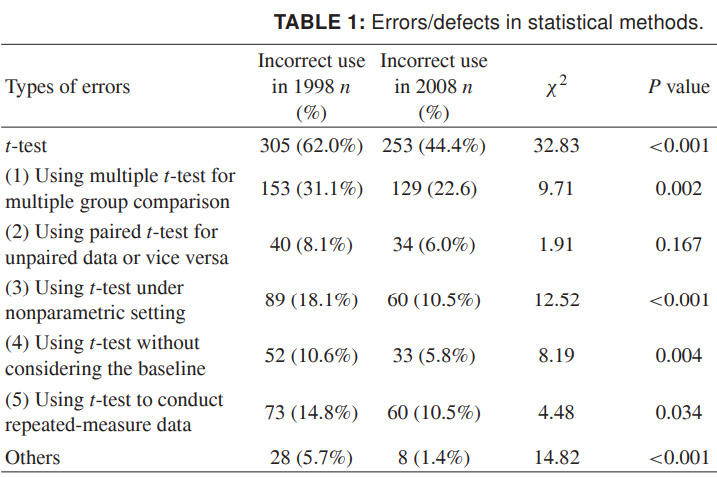
出典： 1998年および2008年の10の主要な中国医学雑誌における統計的手法の誤用。ShunquanWu et al、The Scientific World Journal、2011、11、2106–2114

結果の重要性が低いことは、誤った結果ほど悲しいことではないことを忘れないでください。 誤った統計を適用してデータをゆがめることにより、科学的な罪（誤った結論）をもたらすことは不可能です。

統計データの誤った解釈を含む論理的解釈については、おそらく個別に伝えます。

正しく読んでください。