⤴️ 🗞️ ⭕️ リレーショナルプログラミング：痛み、興味、そして痛み 👩🏿‍✈️ 🤕 ◽️

前回の投稿では、「産業用プログラミング」の分野で学生に教えていることを詳細に説明しました。たとえば、プログラミングの理論研究で使用される新しいプログラミングパラダイムや抽象数学に興味がある、より理論的な分野に関心のある分野には、「プログラミング言語」という別の専門分野があります。

今日、私は大学で、また言語ツールJetBrains Researchの研究室で学生研究者として行っているリレーショナルプログラミングの分野での私の研究についてお話します。

リレーショナルプログラミングとは何ですか？通常、引数を指定して関数を実行し、結果を取得します。そして、リレーショナルの場合、反対のことができます：結果と1つの引数を修正し、2番目の引数を取得します。主なことは、コードを正しく記述し、忍耐強く、良好なクラスターを持つことです。

私自身について

私の名前はDmitry Rozplohasで、サンクトペテルブルクHSEの1年生です。昨年、「プログラミング言語」の分野でアカデミック大学の学士課程を卒業しました。学部3年生以来、私はJetBrains Research言語ツール研究室の研究生でもあります。

リレーショナルプログラミング

一般的な事実

リレーショナルプログラミングは、関数の代わりに、引数と結果の関係を記述する場合です。言語がこのために強化されている場合、特定のボーナス、たとえば、関数を反対方向に実行する機能（結果として引数の可能な値を復元する）を取得できます。

一般に、これは任意の論理言語で行うことができますが、約10年前にミニマルな純粋論理言語miniKanrenの出現と同時にリレーショナルプログラミングへの関心が生じ、そのような関係を簡単に記述して使用できるようになりました。

最も高度なユースケースの一部を次に示します：プルーフチェッカーを作成してそれを使用して証拠を見つける（ Near et al。、2008 ）、または特定の言語のインタープリターを作成してテストスイートプログラムを生成する（ Byrd et al。、2017 ）ことができます。

構文とおもちゃの例

miniKanrenは小さな言語であり、関係を記述するために使用されるのは基本的な数学的構造のみです。これは埋め込み言語であり、そのプリミティブは外部言語のライブラリであり、小さなminiKanrenプログラムは別の言語のプログラム内で使用できます。

miniKanrenに適した外国語。当初、Schemeがあり、Ocaml（ OCanren ）のバージョンで作業しています。完全なリストはminikanren.orgで見ることができます。この記事の例はOCanrenにもあります。多くの実装はヘルパー関数を追加しますが、コア言語のみに焦点を合わせます。

データ型から始めましょう。従来、これらは2つのタイプに分類できます。

定数は、埋め込み先の言語のデータです。文字列、数字、さらには配列。しかし、基本的なminiKanrenの場合、これはすべてブラックボックスであり、定数は等しいかどうかのみをチェックできます。
「用語」は、いくつかの要素のタプルです。 Haskellのデータコンストラクターと同じ方法で一般的に使用されます：データコンストラクター（文字列）プラス0個以上のパラメーター。 OCanrenは、OCamlの通常のデータコンストラクターを使用します。

たとえば、miniKanren自体で配列を使用する場合は、関数型言語と同様の用語で、単一リンクリストとして記述する必要があります。リストは、空のリスト（単純な用語で示される）、またはリストの最初の要素のペア（「head」）と他の要素（「tail」）のいずれかです。

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil)))

miniKanrenプログラムは、いくつかの変数間の関係です。起動時に、プログラムは変数のすべての可能な値を一般的な形式で提供します。多くの場合、実装では、出力の回答数を制限できます。たとえば、最初の回答のみを検索します。すべてのソリューションを検索した後、検索が常に停止するとは限りません。

相互に定義され、関数として再帰的に呼び出される複数の関係を作成できます。たとえば、以下の関数の代わりに

a p p e n d （ a 、 b ） \to と

$append（a、b）→と$ 関係を定義する

a p p e n d o （ a 、 b 、 c ）

$appendo（a、b、c）$ ：リスト

c

$c$ リストの連結です

a

$a$ そして

b

$b$ 。従来、関係を返す関数は、通常の関数と区別するために「o」で終わります。

関係は、その引数に関する何らかのステートメントとして記述されます。 4つの基本操作があります。

2つの用語の統一または等価（===）。用語には変数を含めることができます。たとえば、リレーション「リスト

l

$l$ 1つの要素で構成されます

x

$x$ 」：

 let isSingletono xl = l === Cons (x, Nil)

論理積（論理「and」）および分離（論理「or」）-通常の論理のように。 OCanrenは&&&および|||と呼ばれます。しかし、MiniKanrenには基本的に論理否定はありません。

新しい変数を追加します。論理的には、それは存在の量指定子です。たとえば、空でないリストをチェックするには、リストがヘッドとテールで構成されていることをチェックする必要があります。これらは関係の引数ではないため、新しい変数を作成する必要があります。

 let nonEmptyo l = fresh (ht) (l === Cons (h, t))

関係は、それ自体を再帰的に呼び出すことができます。たとえば、「要素」という関係を定義する必要があります

x

$x$ リストに載っています。」関数型言語のように、些細なケースを分析することでこの問題を解決します。

または、リストの先頭は $x$
どちらか $x$ 尾にある

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) )

言語の基本バージョンは、これら4つの操作に基づいて構築されています。他の操作を使用するための拡張機能もあります。最も有用なのは、2つの用語の不等式（= / =）を設定するための不等式制約です。

ミニマリズムにもかかわらず、miniKanrenは非常に表現力豊かな言語です。たとえば、2つのリストのリレーショナル連結を見てください。 2つの引数の関数は、三重の関係になります "

a b

$ab$ リストの連結です

a

$a$ そして

b

$b$ 「。

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb)))

ソリューションは、関数型言語で記述する方法と構造的に違いはありません。節によって結合された2つのケースを分析します。

最初のリストが空の場合、2番目のリストと連結の結果は等しくなります。
最初のリストが空でない場合は、リストを先頭と末尾に解析し、リレーションの再帰呼び出しを使用して結果を作成します。

最初の引数と2番目の引数を修正することにより、この関係にリクエストを行うことができます-リストの連結を取得します：

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))

最後の引数を修正できます-このリストのすべてのパーティションを2つに分割します。

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil)))))

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil

他に何でもできます。引数の一部のみを修正するもう少し非標準的な例：

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))

⇒

 q = 2, r = Cons (3, Cons (4, Nil))

仕組み

理論の観点からは、ここで印象的なことは何もありません：すべての引数のすべての可能なオプションの列挙を開始するだけで、各セットが特定の関数/関係に関して希望どおりに動作するかどうかを確認できます（「The British Museum Algorithm」を参照）。ここで興味深いのは、ここでの検索（言い換えると、ソリューションの検索）が記述された関係の構造のみを使用するという事実です。そのため、実際には比較的効果的です。

検索は、現在の状態のさまざまな変数に関する情報の蓄積に関連しています。各変数について何も知らないか、用語、値、その他の変数でどのように表現されるかを知っています。例：

b = Cons (x, y) 
      

        
        
        
      

     c = Cons (10, z) 
      

        
        
        
      

     x = ? 
      

        
        
        
      

     y = ? 
      

        
        
        
      

     z = ?

統一を経て、この情報を念頭に置いて2つの用語を調べ、2つの用語を統合できない場合は状態を更新するか、検索を終了します。たとえば、統一b = cを完了すると、x = 10、y = zという新しい情報が得られます。しかし、統一b = Nilは矛盾を引き起こします。

連続して（情報が蓄積するように）検索し、分離して、検索を2つの並列ブランチに分割し、それらのステップを交互に進めます-これはいわゆるインターリーブ検索です。この交互のおかげで、検索は完了しました-有限時間後にすべての適切なソリューションが見つかります。たとえば、Prolog言語ではそうではありません。ディープクロール（無限分岐にハングアップする可能性があります）のようなことを行います。インターリーブ検索は、本質的にトリッキーなワイドクロールの変更です。

前のセクションの最初のクエリがどのように機能するかを見てみましょう。 appendoには再帰呼び出しがあるため、変数に区別するために変数にインデックスを追加します。次の図は、列挙ツリーを示しています。矢印は、情報伝達の方向を示します（再帰からの戻りを除く）。選言の間では、情報は分配されず、接続詞の間では左から右に分配されます。

appendoへの外部呼び出しから始めます。論争のために分離の左の枝が死ぬ：リスト $a$ 空ではありません。
右側の分岐には、補助変数が導入され、リストを「解析」するために使用されます $a_1$ 頭と尾に。
その後、a = [2]、b = [3、4]、ab =？に対して、付録の再帰呼び出しが発生し、同様の操作が発生します。
しかし、3回目のappendoの呼び出しでは、a = []、b = [3,4]、ab =？があり、左の選言が機能するだけで、その後にab = bの情報が得られます。しかし、右の枝には矛盾があります。
これで、利用可能なすべての情報を書き出し、変数の値を代入することで答えを復元できます。

a_1 = [1, 2] b_1 = [3, 4] ab_1 = Cons h_1 tb_1 h_1 = 1 a_2 = t_1 = [2] b_2 = b_1 = [3, 4] ab_2 = tb_1 = Cons h_2 tb_2 h_2 = 2 a_3 = t_2 = Nil b_3 = b_2 = b_1 = [3, 4] ab_3 = tb_2 = b_3 = [3, 4]
それに続く $ab_1$ =短所（1、短所（2、[3、4]））= [1、2、3、4]、必要に応じて。

学部でやったこと

すべてが遅くなります

いつものように、彼らはすべてが超宣言的であることを約束しますが、実際には、少なくとも何かが機能するためには、最も単純な例を除いて、言語に適応し、特別な方法ですべてを書く必要があります（すべてが実行される方法を念頭に置いて）。これは残念です。

初心者のminiKanrenプログラマが直面する最初の問題の1つは、プログラムで条件（接続詞）を記述する順序に大きく依存することです。 1つの注文ですべては問題ありませんが、2つの接続詞が入れ替わり、すべてが非常にゆっくりと動作し始めるか、まったく終了しませんでした。これは予想外です。

付録の例でも、反対方向への起動（リストを2つに分割）は、必要な回答の数を明示的に指定しない限り終了しません（必要な数が見つかると検索が終了します）。

元の変数を次のように修正するとします：a = ?, B = ?, Ab = [1、2、3]（下図を参照）2番目のブランチでは、この情報は再帰呼び出し中に使用されません（変数abと

h_{1}

$h_1$ そして

t b_{1}

$tb_1$ この呼び出しの後にのみ表示されます）。したがって、最初の再帰呼び出しでは、その引数はすべて自由変数になります。この呼び出しは、2つのリストとその連結からすべての種類のトリプルを生成し（この生成は終了しません）、その中から3番目の要素がまさに必要なものを選択します。

大規模なグループでこれらのトリプルを並べ替えるので、すべてが一見すると思われるほど悪くはありません。長さが同じで要素が異なるリストは、関数の観点からはまったく変わらないため、1つのソリューションに分類されます。要素の代わりに自由変数があります。それでも、必要なリストの長さをすべて並べ替えますが、必要なのは1つだけで、どの長さかはわかっています。これは、検索における情報の非常に非合理的な使用（非使用）です。

この特定の例は簡単に修正できます。再帰呼び出しを最後に移動するだけで、すべてが正常に機能します。再帰呼び出しの前に、変数abとの統合が行われ、指定されたリストの末尾から再帰呼び出しが行われます（通常の再帰関数として）。再帰呼び出しを最後に持つこの定義は、すべての方向でうまく機能します。再帰呼び出しまで、引数に関するすべての可能な情報を蓄積することができます。

ただし、少し複雑な例では、いくつかの意味のある呼び出しがある場合、すべてが正常になる特定の順序は存在しません。最も単純な例：連結を使用してリストを展開します。最初の引数を修正します-この特定の順序が必要です。2番目の引数を修正します-呼び出しを交換する必要があります。それ以外の場合は、長時間検索され、検索は終了しません。

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr))

これは、インターリーブ検索が連続して接続詞を処理し、試行したものの許容可能な効率を損なうことなく異なる方法を思い付くことができないためです。もちろん、すべての解決策はいつか見つかるでしょうが、間違った順序で、それらは非常に非現実的に長く検索されるため、実用的な意味はありません。

この問題を回避するためのプログラムを作成する手法があります。しかし、それらの多くは使用するために特別なスキルと想像力を必要とし、結果は非常に大きなプログラムです。例は、用語サイズの境界技術と、その助けを借りた乗算による剰余を伴うバイナリ除算の定義です。数学的な定義を愚かに書く代わりに

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm))

20行の再帰的な定義と、読むのが現実的ではない大きな補助関数を書かなければなりません（そこで何が行われているのかまだわかりません）。それは、純粋な二項算術セクションのウィルバードの論文にあります。

上記を考慮して、単純で自然に書かれたプログラムも動作するように、何らかの検索の変更を考えたいと思います。

最適化

すべてが悪い場合、回答の数を明示的に指定して中断しない限り、検索が終了しないことに気付きました。そのため、彼らは検索の不完全性と正確に戦うことにしました。具体化するのは「長期にわたって機能する」よりもはるかに簡単です。一般に、もちろん、検索の速度を上げたいだけですが、形式化するのははるかに難しいので、野心的なタスクから始めました。

ほとんどの場合、検索が分岐すると、追跡しやすい状況が発生します。特定の関数が再帰的に呼び出され、再帰呼び出しで、引数が同じかそれより具体的でない場合、再帰呼び出しで別のそのようなサブタスクが再び生成され、無限再帰が発生します。正式には、次のように聞こえます。置換があり、それを新しい引数に適用して、古い引数を取得します。たとえば、次の図では、再帰呼び出しは元の呼び出しを一般化したものです。

c_{2}

$c_2$ = [x、3]、

d_{2}

$d_2$ = xおよび元の呼び出しを取得します。

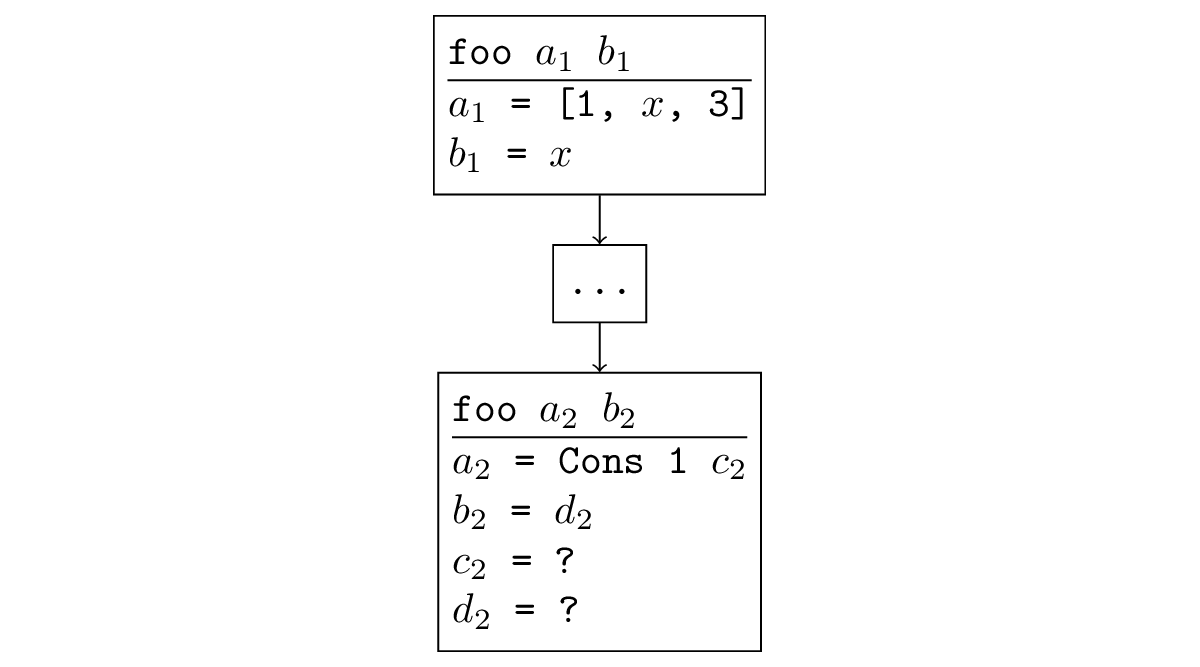
このような状況は、すでに出会った分岐の例でも発生していることがわかります。前に書いたように、逆方向にappendoを実行すると、すべての変数の代わりに自由変数を使用して再帰呼び出しが行われます。もちろん、3番目の引数が修正された元の呼び出しよりも具体的ではありません。

x =？でレベルソを実行するとそしてxr = [1、2、3]、最初の再帰呼び出しが2つの自由変数で再び発生することがわかります。そのため、新しい引数は明らかに以前の変数に再び転送できます。

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *)

この基準を使用して、プログラム実行のプロセスの相違を検出し、この順序ですべてが悪いことを理解し、動的に別の順序に変更できます。これにより、理想的には、各コールに対して正しい順序が選択されます。

素直にそれを行うことができます。分岐点で分岐が見つかった場合、彼がすでに見つけたすべての答えを打ち込み、実行を延期して、次の分岐点を「スキップ」します。そして、おそらく、それを実行し続けると、より多くの情報がすでに知られ、相違は生じません。この例では、これにより目的のスワップ接続が得られます。

たとえば、すでに行われた作業を失うことなく、パフォーマンスを延期することを可能にする単純な方法があります。順序を変更する最も愚かな変種がすでにありますが、以下のような既知の接続詞の非可換性に苦しんでいるすべての単純な例で、発散は消えました。

番号のリストの並べ替え（リストのすべての順列の生成でもあります）、
ペアノ算術とバイナリ算術、
指定されたサイズのバイナリツリーの生成。

これは予想外の驚きでした。分岐に加えて、最適化はプログラムのスローダウンとも戦います。以下の図は、2つの異なる順序を組み合わせたプログラムの実行時間を示しています（相対的に言えば、最高の1つと多くの悪い1つ）。 Ubuntu 16.04オペレーティングシステムを搭載したIntel Core i7 CPU M 620、2.67GHz x 4、8GB RAMの構成のコンピューターで起動しました。

順序がすでに最適化されている場合（手動で選択します）、最適化により実行速度が少し遅くなりますが、重要ではありません

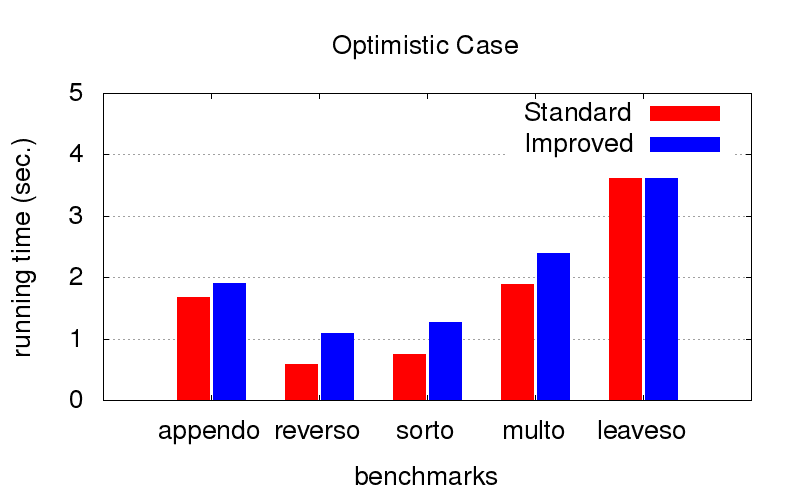
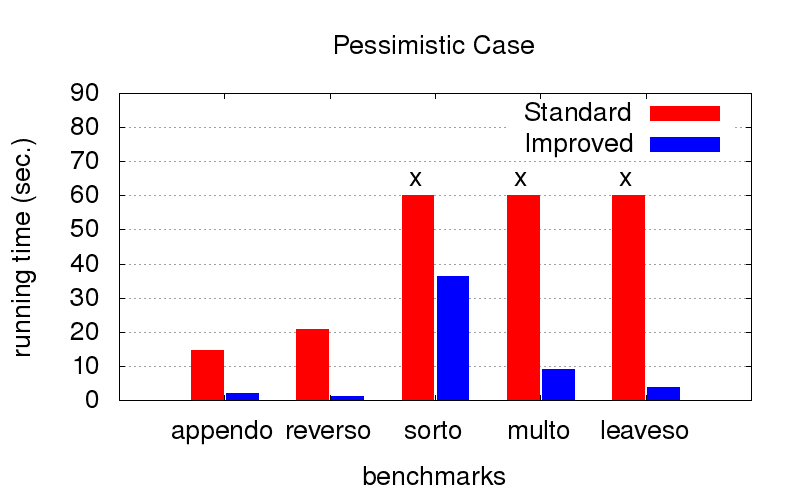
ただし、 順序が最適でない場合（たとえば、反対方向での起動にのみ適している場合）、最適化を使用すると、はるかに高速になります。十字は、終わりを待つことができなかったことを意味します。

何も壊さない方法

これらはすべて、純粋に直感に基づいており、厳密に証明したかったのです。結局のところ理論。

何かを証明するためには、言語の形式的な意味論が必要です。 miniKanrenの操作上のセマンティクスについて説明しました。これは、実際の言語実装の簡略化され数学化されたバージョンです。非常に限られた（したがって使いやすい）バージョンを使用し、プログラムの最終実行のみを指定できます（検索は最終的なものでなければなりません）。しかし、私たちの目的にとって、これはまさに必要なものです。

基準を証明するために、補題が最初に定式化されます。より一般的な状態からのプログラム実行はより長く機能します。正式：セマンティクスの出力ツリーの高さは大きくなります。これは帰納法によって証明されますが、ステートメントは非常に慎重に一般化する必要があります。そうしないと、帰納法の仮説が十分に強くなりません。この補題から、プログラムの実行中に基準が機能した場合、出力ツリーはそれ以上の高さのサブツリーを持つことになります。帰納的に与えられたセマンティクスではすべてのツリーが有限であるため、これは矛盾をもたらします。したがって、私たちのセマンティクスでは、このプログラムの実行は表現できないため、このプログラムでの検索は終了しません。

提案された方法は保守的です。すべてがすでに完全に悪く、悪化させることは不可能であると確信した場合にのみ、何かを変更します。したがって、プログラムの完了に関しては何も壊しません。

メインプルーフには多くの詳細が含まれているため、 Coqに書き込むことで正式に検証する必要がありました。しかし、これは技術的に非常に困難であることが判明したため、私たちは熱意を冷やし、奉仕活動でのみ自動検証に真剣に取り組みました。

転記

作業の途中で、学生研究コンペティションのICFP-2017のポスターセッションでこの研究を発表しました。そこで、言語の作成者であるウィル・バードとダニエル・フリードマンに会いましたが、彼らはそれが有意義であり、より詳細に調べる必要があると言いました。ちなみに、ウィルは一般的にJetBrains Researchの研究室と友達です。 miniKanrenに関するすべての研究は、2015年にサンクトペテルブルクでリレーショナルプログラミングのサマースクールを開催したときに始まりました。

1年後、作業をほぼ完全な形式にし、2018年の宣言型プログラミングの原則と実践で記事を発表しました。

大学院で何をしますか

私たちは、miniKanrenの正式なセマンティクスと、そのすべてのプロパティの厳密な証明に引き続き取り組みたいと考えました。文献では、通常、プロパティ（多くの場合、明らかではない）は、例を使用して単純に仮定および実証されていますが、何も証明していません。たとえば、リレーショナルプログラミングのメインブックは質問と回答のリストであり、それぞれが特定のコードに専念しています。インターリーブ検索の完全性のステートメント（これは、標準Prologに対するminiKanrenの最も重要な利点の1つ）でさえ、厳密な表現を見つけることは不可能です。あなたはそのように生きることはできません、私たちは決めました、そして、ウィルから祝福を受けて、私たちは仕事に取り掛かります。

前の段階で開発したセマンティクスには重大な制限があったことを思い出させてください：有限検索のプログラムのみが記述されました。 miniKanrenでは、無限の数の回答をリストできるため、実行中のプログラムにも関心があります。したがって、よりクールなセマンティクスが必要でした。

プログラミング言語のセマンティクスを定義するさまざまな標準的な方法がありますが、そのうちの1つを選択し、特定のケースに適合させるだけで済みました。セマンティクスをラベル付き遷移システムとして説明しました-検索プロセスの可能な状態とこれらの状態間の遷移のセットで、いくつかはマークされています。つまり、検索のこの段階で別の答えが見つかりました。したがって、特定のプログラムの実行は、そのような遷移のシーケンスによって決定されます。これらのシーケンスは、プログラムの終了と完了を同時に記述しない有限（最終状態になる）またはエンドレスにすることができます。そのようなオブジェクトを数学的に完全に指定するには、共帰納的定義を使用する必要があります。

上記のセマンティクスは操作可能です -これは、検索の実際の実装を反映しています。それに加えて、言語プログラムおよび構成の一部の数学的オブジェクトを自然なプログラムに関連付ける表示的セマンティクスも使用します（たとえば、プログラム内の関係は用語セット上の関係と見なされ、接続詞は関係の交差点などです）。このようなセマンティクスを定義する標準的な方法は、最小のエルブランモデルと呼ばれ、miniKanrenの場合は既に以前に行われています（私たちの研究室でも）。

その後、言語の検索の完全性、および正確性は、これら2つのセマンティクスの同等性として定式化できます。つまり、特定のプログラムに対する回答のセットの一致です。私たちはそれを証明することができました。おもしろい（そして少し悲しい）が、異なるパラメーターでいくつかの入れ子になった誘導を使用して、共誘導なしでやったことです。

当然の結果として、いくつかの有用な言語変換（得られたソリューションのセットに関して）の正確性も取得します：変換が明らかに対応する数学的オブジェクトを変更しない場合、例えば、接続詞の並べ替え、または分配接続詞または選言の使用、検索結果は変更されません。

ここで、セマンティクスを使用して、言語のその他の有用なプロパティ、たとえば、完全性/分岐性の基準、または追加の言語構成の正確性を証明したいと考えています。

また、Coqを使用した形式化の厳密な説明についても詳しく調べました。多くのさまざまな困難を克服し、多大な努力を注いだ結果、言語の操作上のセマンティクスを設定し、いくつかの証拠を実施することができました。Qed。」私たちは自分自身への信仰を失いません。

リレーショナルプログラミング：痛み、興味、そして痛み