ゴールドフェルド仮説に関するアレクサンダー・スミスの研究は、楕円曲線の基本的な性質を明らかにしました
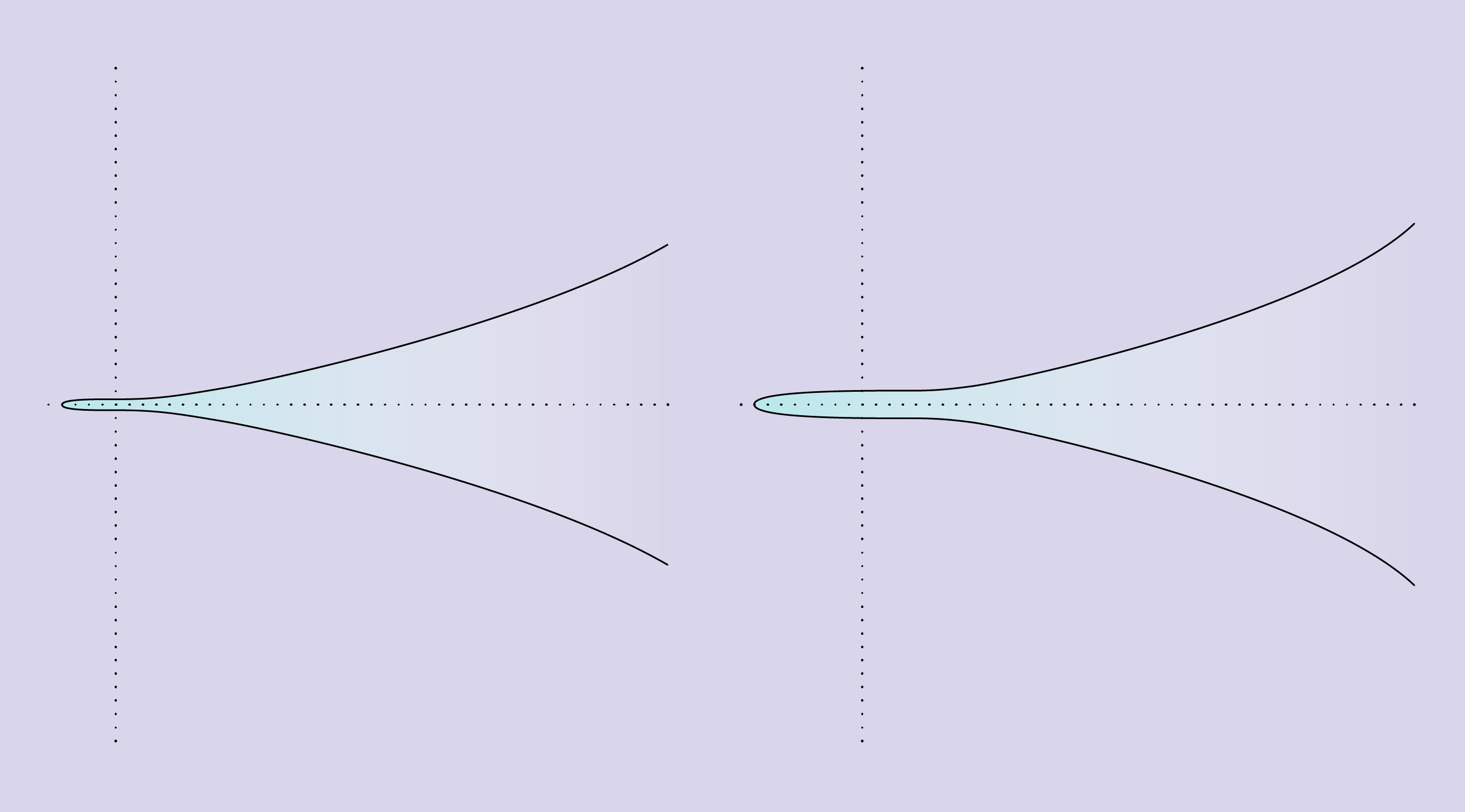
2つの楕円曲線は、ランクの概念の奇妙さを示しています。 左側の曲線は方程式y 2 = x 3 + 1で記述され、5つの有理点のみを通過し、ランク0を持ちます。右側の曲線は方程式y 2 = x 3 + 8で記述され、無数の有理点を通過し、ランク1を持ちます。
楕円曲線にはさまざまなバリエーションがありますが、実際のバリエーションは2つしかありません。 これは、ハーバード大学の大学院生が受け取った新しい証拠の結果です。
楕円曲線はエキゾチックに見えますが、これらは目立たない幾何学的なオブジェクトであり、直線、放物線、または楕円よりも複雑ではありません。 Alexadr Smithは、昨年オンラインで公開された作品で、ランクの楕円曲線の基本的な特徴に関する40年前の仮説を証明しました。 スミスは、1つの特性を持つ特定の曲線ファミリの半分はランク0、半分はランク1であることを証明しました
この結果は、何世紀にもわたって数学者を占領してきたオブジェクトのサポート特性を確立し、その重要性は最近数十年で特に高まっています。
「私たちはこれについて1000年以上も考えてきましたが、今では確率曲線で楕円曲線を理解しています。 これは非常に重要です」と、プリンストン大学の数学者であるショーウー・チャンは、彼がまだプリンストンの学生だったときに彼の作品についてスミスに助言を与えました。
楕円曲線は、変数を3乗した方程式、たとえばy 2 = x 3 + 1です。これらは、1994年のフェルマーの大定理の最も重要な証明を含む、最近数十年で多くの重要な数学的証明に登場しました。 それらの重要性の一部は、数学者が何らかの体系的な考えを持っている最も複雑なタイプの多項式に属するという事実にあります。
「楕円曲線は興味深い事例です」と、コロンビア大学の数学者であるドリアン・ゴールドフェルドは言いました。
Goldfeld仮説は、楕円曲線のランクについて予測を行います。 すでに最近の記事で説明したように、「 厳密な証明がない場合、数学者を説得できる証拠は何ですか? 」ランクは、曲線の有理解のセット(分数として表すことができる解)の複雑さの尺度です。 そして、曲線のランクに証明された制限はありませんが(これまで28最高が最高ランクと見なされます)、ゴールドフェルドの仮説は、楕円曲線の平均半分がランク0で、残りの半分が1であると予測します。
楕円曲線の半分にランク0があり、残りの半分に1がある場合、1を超えるランクの楕円曲線がどのように存在するかは明らかではないようです。ピンポンボールの箱があり、その正確に半分がわかっている場合それらは黒で、半分は白で、赤いものはあり得ません。
さらに紛らわしいのは、ランクが2以上の楕円曲線が少数ではなく無限に存在するという事実です。 一見不合理な結果は、無限で動作するcな統計の結果です。 ランク2以上の曲線は多数ありますが、ランク0および1の曲線は非常に多く、ランク2以上の曲線は統計的に有意ではありません。 すべての曲線をボックスに入れ、そこからランダムに取り出した場合、ランクが1を超える曲線を引き出す可能性は公式にゼロに等しくなります。
曲線のランクが0であることはどういう意味ですか? このような曲線は、 バリーマズールが1970年代に証明したように、有限数の合理的なポイントを持ち、16を超えません。

ドリアン・ゴールドフェルド
非常に多数の楕円曲線のランクが0であると信じる理由があります。平面に沿って曲線がどのように走るかを想像すると、通過する点のほとんどが合理的ではないことがわかります。 これらの点は、たとえ任意に複雑であっても、分数として表すことはできません。 ランダムな曲線が多くの合理的なポイントと交差する可能性は-無限のセット-小さなです。
「このように考えます。ランダムな楕円曲線をとると、ランクが0になる理由があります。合理的な点を持ちたくないのです」とスミス氏は言います。
ランク1曲線の有病率は、同様の方法で説明されます。 ランク1の曲線には無数の有理点がありますが、それらはすべて非常にきれいに整列されているため、かなり簡単なプロセスでそれらを相互に接続できます。
ランク2以上の曲線の場合、有理点のセットはより複雑です。 それらには、互いに接続されていない合理的な点の無限のサブセットがいくつか含まれています。
「2つの独立したポイントが現れる可能性はどのくらいですか? -ゴールドフェルドは言った。 「非常に低い。」 私の仮説では、これはめったに起こらないはずだと言っています。」
ゴールドフェルドが最初に仮説を提唱したとき、ほとんどの数学者はそれを間違っていると考えていました。 彼らは計算実験の結果を指摘し、その後、ランクが2以上の曲線はケースの0%よりもはるかに頻繁に発生することを示しました。
ゴールドフェルドは、彼らは単に範囲が小さすぎると答えた。 彼は、最初の10個の整数だけを調べれば、数字の40%が素数であるという非常に不正確な推定値を得ることができると指摘しました。 同様に、これらの計算実験は、楕円曲線の小さなサブセットから無限に大きな曲線のファミリーに外挿しました。
「素数を見て言った! それが私の答えでした。 私たちはもっと高く登る必要があります。なぜなら、最初は多くの楽しみが現れるからです」とゴールドフェルドは語った。
ゴールドフェルドの仮説は、すべての楕円曲線に適用されるわけではありません。 楕円曲線、二次ねじれの特別なファミリを記述します。 例:楕円曲線cy 2 = x 3 -x、ここでcは定数です。 cの値を変更することにより、楕円曲線を曲げます。 ゴールドフェルドの仮説は、cの値を変更することによって得られる無限の多様な曲線全体を指します。
アレクサンダー・スミスは、ゴールドフェルドが正しいと証言した。 新しい論文で、彼は(特別な種類の)楕円曲線の100%が0または1のランクを持っていることを証明しました。また、これらの曲線が2つのランクの間で等しく分割されることを証明しましたが、キャッチがあります。 彼の50–50区分の証明は、 Birch – Swinnerton-Dyer (BSD) 仮説の妥当性に基づいています。 BSD仮説は、数学で最も有名な未解決の問題の1つです。 数学者はまだその証明に近づいていませんが、全体として彼らはそれを真実だと考えています。
その警告があっても、スミスの結果は重要であると考えられます。 数学者によると、彼はBSD仮説を落胆させることなく、Goldfeld仮説を完全に証明する方法を示しているという。 この方法により、楕円曲線の性質を新たに理解できます。
ウィスコンシン大学の数学者であるメラニー・ウッドは、次のように述べています。 「これが証明できるという事実は非常に重要で革命的です。」