新しい統計モデルは、数論からの長い間受け入れられていた仮定を損なうようです。 厳密な証拠だけが本当に重要な場合、あなたは彼女をどれだけ信頼できますか?
楕円曲線y 2 = x 3-4x + 1のどの点が有理ですか? それらを見つけるには、有理点のペアを通して線を引く必要があります。 線が通るすべての点も合理的です。
最近、4人の研究者が研究分野の常識を覆すモデルを考案しました。 彼らは計算データを使用して、基本概念の1つに関する一般的な数十年の見解が誤っていることを示唆しました。
そして、これらは生物学者、気候学者、物理学者ではありません。 彼らの科学分野では、経験的モデルは真実に関して発言権を持っていません。 彼らは数学者であり、規律の代表であり、その標準通貨-否定できない論理的証拠-は通常、他の分野に影響を与える議論から彼らを救います。 そしてまだここにあります。彼らのモデルは、おそらく長年のアイデアのいくつかを修正する時だと言っています。
2016年にオンラインで公開され、Journal of the European Mathematical Societyに掲載される準備ができたモデルは、代数方程式のランクなどの由緒ある数学的概念に属します。 ランクは、方程式の解の数が有理数に関連し、どの解が無理数に関連するかに対応する尺度です。 高ランクの方程式はより合理的な解を持ち、より複雑です。
20世紀初頭から、数学者は方程式の階数の高さに制限があるかどうかの問題に関心を寄せてきました。 最初は、ほとんどの人が制限が存在するべきだと考えていました。 しかし、1970年代までに、一般的な意見は変わりました。ほとんどの数学者はランクが無制限であると信じ始めました。つまり、無限に大きなランクの曲線を検出できるようになりました。 そのため、一部の数学者はこの意見を支持する強い議論はないと信じていましたが、それは起こりました。
「人々は制限がないことについて非常に権威主義的です。 しかし、理解し始めると、この証拠は非常に弱いことがわかります」と、モントリオール大学およびロンドン大学ユニバーシティカレッジの数学者アンドリューグランビルは言いました。
今日、そうでないことを示す証拠があります。 モデルの登場から2年後、彼女は多くの数学者に、特定のタイプの代数方程式のランクが本当に限られていることを確信させました。 ただし、このモデルが説得力があると誰もが考えているわけではありません。 合意の欠如により、数学的な結果とはあまり関係のない質問が発生します。厳密な証拠のみが重要な分野では、経験的証拠はどの程度の重みを持ちますか
「このモデルがまさに私たちが必要とするものであるという数学的な正当性はありません」と、オハイオ大学の数学者であり、研究の共著者であるジェニファー・パークは言いました。 「さらに、実験的な観点から、多くのことが機能します。」
ポイントツーポイント
方程式が与えられた場合、グラフ上にその解の曲線を描くことができます。 数学者は、これらの解のどれだけが合理的であるかを知りたがっています。これらは2つの整数(1/2、-3または4483/929)の比として表現できる数値のタイプに属します。
合理的な解決策を体系的に見つけることは困難ですが、数学者には特定の条件下で機能するテクニックがあります。 方程式x 2 + y 2 = 1を取ります。この方程式の解のグラフは円です。 円のすべての有理点を見つけるために、1つの明確な解法から始めます-たとえば、x = 1およびy = 0の点から。 次に、この点を通る線を描き、他の点で円と交差します。 直線の勾配が合理的な場合、2番目の交点も合理的な解になります。 線を引くことにより、合理的な決定の数を1から2に増やしました。
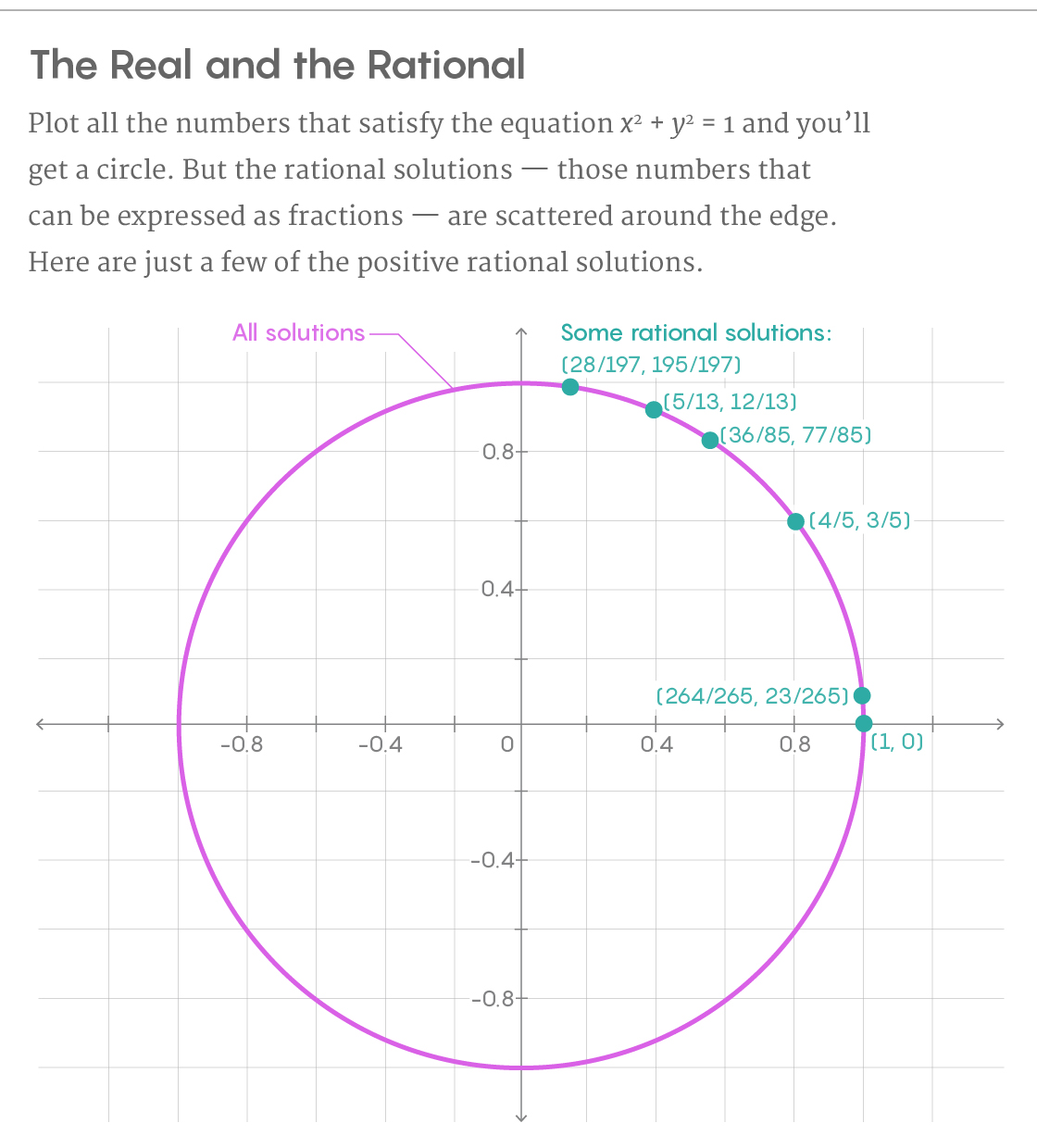
そしてそこで停止する必要はありません。 2番目の有理点を通る別の有理勾配を持つ直線を描くことで手順を繰り返します。これは3番目の有理点で円と交差します。 この方法を無限に続けると、最終的には無限の数の円のすべての有理点を見つけることになります。
また、円の場合は、1つのポイントから開始する必要があり、それらすべてを見つけることができます。 他のすべてを見つけるために最初に知る必要がある合理的な決定の数は、曲線のランクとして知られています。 ランクは、合理的な決定の無限のセットを単一の数で記述するための適切な方法です。 「これは、これらの曲線の合理的な解決策を記述するための最良の方法のようなものです」と、MITの数学者でモデルの共著者であるBjorn Puunen氏は述べました。
円は2次方程式、または2次の方程式です(「次数」は、方程式の項の最大次数の大きさを意味します)。 100年以上にわたり、数学者は2次方程式の合理的な解を見つける方法を知っています。
次のタイプの方程式は楕円曲線であり、3次に引き上げられた変数があります。 楕円曲線は、数学研究の最も魅力的な分野に存在します。 それらは二次方程式よりも複雑です;したがって、それらを研究することは興味深いですが、あまり複雑ではありません。 線を描画するための修正された手順は、楕円曲線にも適用できますが、4次以上の方程式の使用を中止します。
楕円曲線にはさまざまなランクがあります。 一部の楕円曲線では、1つの有理点から開始し、線を描く手順を適用できますが、すべての有理解を見つけることはできません。 1つ目に関連付けられていない2つ目の有理点を追加する必要がある場合があります。 それを使用して、線を描くための新しい手順を開始し、合理的なポイントのバランスを見つけます。 2つの有理点を知る必要があるすべての有理点を見つけるための曲線のランクは、最初は2です。
楕円曲線のランクの高さに制限はありません。 方程式のランクが高いほど、曲線の有理解のセットが広く複雑になります。 「ランクは何らかの形で決定セットの複雑さを測定します」とPuunen氏は述べています。
それにも関わらず、ランクは数学者が理論で説明しようとする試みを免れます。 楕円曲線が与えられた場合、その外観とランクとの間に明らかな関係はありません。 「楕円曲線があり、係数を少し調整すると、ランクが根本的に変わります」とパークは言いました。 -係数を1つずつ変更すると、ランクが100万にジャンプします。 ランクの振る舞いは誰にもわかりません。」
一般理論の欠如により、数学者はランクの制限の存在について推測するために持っている証拠の小さなセットに後退するようになりました。 「視点は、ランクに制限がないということです。人々は常にますます高いランクを見つけているからです」とグランビルは言いました。 現在の記録保持者は、2006年にハーバード大学の数学者Noam Elkisによって発見されたランク28の楕円曲線です。
しかし、その後、この新しいモデルが登場し、ほぼ確実に道の終わりであると述べました。
21で驚き
科学者は、直接的な研究には複雑すぎるかアクセスできない現象を研究するために、モデルを使用します。 実験室でブラックホールの類似物を作成したので、彼らはイベントの地平線の端に沿って歩く必要なしに本当のブラックホールがどのように振る舞うかについて何かを学ぶことができるかもしれません。
数学者も同じことをします。 良い例は素数の研究です。 数学者は双子の素数に関する質問への答えを知りたい-2(3と5、11と13)異なる素数のペアが無限にあります。 徹底的な答えは知識を超えていますが、双子の数の頻度を予測するモデルを作成しました。そして、答えは無限に発生するということです。
新しいモデルは、楕円曲線自体を直接研究しません。 彼女はマトリックスコアのような数学的な対象を探ります。 核は楕円曲線を指します。マウスと人間は同じものではありませんが、研究が容易であり、他の実験に基づいていくつかの結論を導き出すのに十分近いことが望まれます。 特に、カーネルには独自のバージョンのrankがあります。 核のランクの分布-ランク1の核の数、ランク2の核の数などを研究した後、4人の数学者は楕円曲線のランクの分布のアイデアを得ることを望みました。 実際、彼らは核と楕円曲線のランクの分布が互いに類似していることに賭けています。

ジェニファー・パーク、ビョルン・プーネン、メラニー・ウッド
「信仰の飛躍が始まります」とパークは語った。 「おそらく、もっと理解しやすく、楕円曲線と同じランク分布を持つ数学的オブジェクトの別のセットがあることを願っています。」
4人の研究者がこの作業を行ったとき、ほとんどの数学者はランクに制限がないと考えていました。 しかし、モデルは別の話をしました。 彼女は、21を超えるランクの楕円曲線は有限数しかないと言います。有限数の楕円曲線がある場合、そのうちの1つが最高ランクになります。つまり、ランクにはまだ上限があります。 4人の数学者がこれを見たとき、彼らは自分たちの手に生きた結果があることに気づきました。
「この予測は、誰もが信じていたもの、少なくとも公に認めたものと一致しませんでした」とウッド氏は言いました。 「ランクに制限があるとは誰も信じていませんでした。」
モデルへの信頼がかなり深刻なステップを必要とする場合、モデルが常識が間違っていると報告したとき、さらに大きなステップが必要です。 ただし、この結果を支持する多くの証拠があります。 このモデルは、楕円曲線のさまざまな特性を研究した他の数学者によって作成された以前のモデルに基づいています。 これらのモデルは時の試練に耐えてきました。 これらの予測のいくつかは証明されています。
「ゼロから始めて新しいモデルを作ることを提案する人はいませんでした」とウッドは言いました。 「問題は、人々がすでに信じている既存のモデルをどのように充実させるかでした。」
モデルを信じるもう1つの理由は、ランク値21が任意の境界とは思われないことです。 10年前に、グランビルは別のモデルを作成しました。このモデルから、ランクが21を超える楕円曲線は限られているはずです。グランビルモデルは現在のものとまったく類似していませんでした。多くの数学者の観点からの単なる偶然の一致とはまったく異なります。
「2つの完全に異なるヒューリスティックモデルがあり、どちらも同じ数21を与えました。これは人々を驚かせました」とパークは言いました。
おそらく、モデルが信頼できると思われる最も説得力のある理由は、他の予測が楕円曲線の実証済みの特性とほぼ正確に一致したという事実でした。 モデルの一般化された結論-ランクが21を超える有限数の楕円曲線の存在-は、すべての楕円曲線に適用されます。 しかし、彼らには特定のファミリーがあり、その多くはすでに数学者がランクの境界を決定しています。 モデルは、これらの多くのファミリーのランク値も予測しました。その予測は、数学者がすでに決定した境界と類似していたか、または正確に一致していました。
「私たちの国境は、他の人々によって研究されたすべてのケースを正確に予測していました」とパークは言いました。 「人々は私の報告について懐疑的ですが、他の偶然の一致について言及するとき、彼らはこれに非常に驚いています。」
証拠と証拠の間
モデルには多くのサポートがありますが、誰もがそれを信じているわけではなく、間違っている可能性があります。 最も重要な懐疑論者は、楕円曲線のランク記録を樹立したハーバードの数学者、ノアム・エルキスです。 ハーバード大学で最年少のフルタイム教授になった数十年の間に、彼はランク境界の欠如を示すいくつかの結果を受け取りました。 「私の意見は長い間変わっていません。特定の仮説を支持するためにこの問題に精通しているとは思わない」とエルキスは私に手紙で書いた。
Elkisは、このモデルは多くの点で正しく機能しない可能性があると考えています。 ランダムに選択された曲線を考慮するか、何らかの意味で曲線は平均的です。 ただし、エルキス自身の研究など、楕円曲線のファミリーが存在する可能性についての証拠があります。それぞれの楕円曲線には無限の数のそのような曲線が含まれ、その動作は典型的な曲線の動作とは大きく異なります。 「ランダムカーブの予想される動作に基づいたヒューリスティックモデルは、極端な動作についてのストーリー全体を伝えるとは限りません」とElkis氏は書いています。
モデルの作成者の1人でさえ、完全には確信がありません。 「私は、不可知論者のようにランクが制限されていると言うでしょう」とウッドは言いました。 彼女は、エルキスによって表明された理由により、モデルが間違っている可能性があることを認めています。 ただし、モデルがタスクに対応していない場合、楕円曲線のいくつかの隠れた予期しない特性を考慮していないためです。 「問題は、ランクが限られていると信じていない場合、どの場所でモデルが機能しなくなるのかということです」とウッド氏。
「最も可能性が高いのは、誰かが間違っている理由を賢明な理由で見つけられない場合、彼らは正しいでしょう。 そのような理由が存在するかどうかはわかりません」と、ハーバード大学の大学院生で、エルキスと協力して楕円曲線のランクを研究しているアレクサンダー・スミスは言いました。
モデルの作者は、その重要性を教義に高めません。 彼らは証拠と証拠の違いを知っており、前者の山が後者に通じないことを理解しています。 しかし、彼らは、少なくとも1世紀の単純な推論の後、基本的に数学的概念を熟考するための理にかなった基盤を提供すると信じています。
「おそらく、高次の楕円曲線を見つけることは数学者にとっての挑戦です」と、パークは言いました。 あるいは、おそらく、数学者は「一般的な仮説として、私たちが信じていたものについての彼らの意見を再考すべきです」。