前の記事で、パラメトリック最適化の方法の比較、つまりパラメーターの選択、後続のバックテスト中のロボット取引の収益性の評価を開始しました。ロボットパラメーターのランダムな無相関の組み合わせの生成である、通常のモンテカルロ法が非常にうまく機能することが判明しました。次に、プログラミングトレーダーのコミュニティにある遺伝的最適化アルゴリズムなど、一般的なアルゴリズムをテストします。

取引戦略を最適化するための遺伝的アルゴリズム

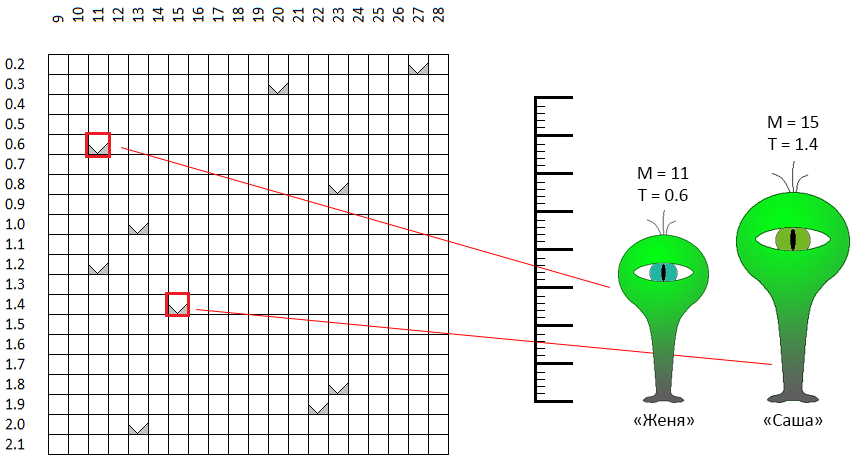
このアルゴリズムは、2つのパラメーターの最適化の例として考えます。ロボットの最適化されたパラメーターは、移動平均とTakeProfitの期間です。「遺伝学」をさらに深く理解するために、移動平均の期間を「成長」の原因となる遺伝子と呼び、TakeProfit-「目の色」の遺伝子と呼ぶことに同意します。

許容されるパラメータ値のスペースでは、各ポイント、座標の各ペア-「高さ/目の色」は理論的には1つの「個人」を表します。 10人の個人をランダムに作成したとします。これは、遺伝的最適化アルゴリズムの最初のステップでした -第一世代を作成します。

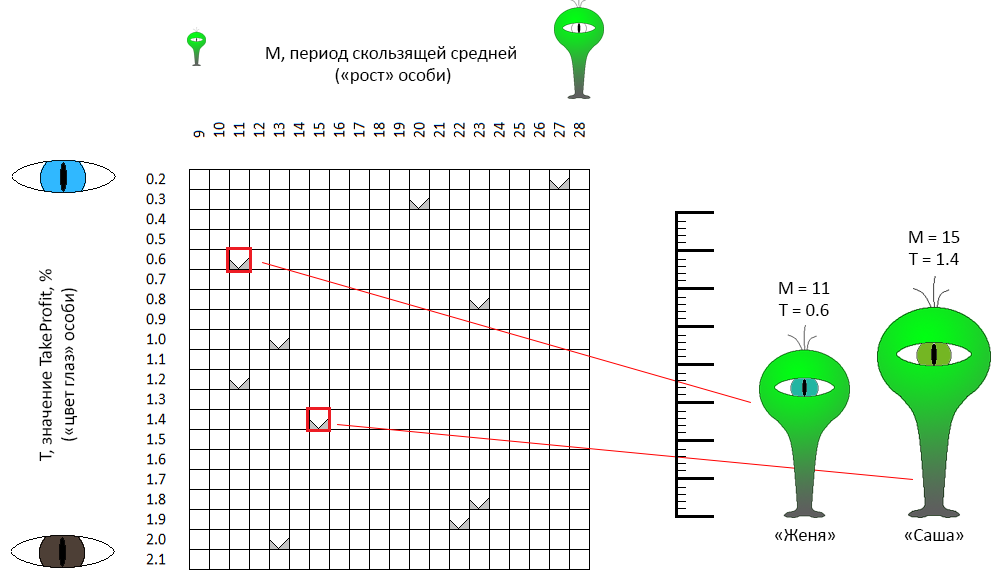
座標空間M-Tでは、ポイントがランダムに選択されます。たとえば、赤い枠でマークされた2つのドットは、性別に依存しない名前を持つ「個人」です（これは重要なポイントです！）ジェンヤとサーシャ。サーシャの「成長」（問題の最初の定式化では移動平均期間）は11単位、「目の色」は0.6（青緑の目）です。 Zhenyaはパラメーターがわずかに異なります。同じ特性が残りの8人の個人を説明しています。

次のステップは再生です

第一世代全体から、一定数の最も「成功した」個人を特定します。基準は明らかにCFの値です。これらの個体は繁殖し、ランダムにペアを形成します（このため、性別に依存しない名前を受け取りました）一般に、一致するペアに対して多くのルールを設定できます。たとえば、特性に近い（つまり、文字通り、座標空間で最も近い）個体を選択する-近親交配。それどころか、反対（異系交配）を探すことができます。私はこれらのオプションのいずれかを支持する引数を見つけることができませんでした-私の実装では、ペアは偶然に厳密に形成されます... 私たちの文脈でこれはどういう意味ですか？

2人の「親」個人から3番目の個人を取得します。これは、一方の親の特性の一部、他方の一部の特性を継承します。たとえば、ジェンヤとサーシャは個々のニキータ（ニキータ、ニキータ？）を出産しました。

ニキータは両親の1人である「Zhenya」から「目の色」（ロボットのTakeProfitパラメータ）の記号を継承しました。
「成長」（移動平均ロボットの期間）ニキータは「サーシャ」から継承しましたが、別の親であるジェンヤの方向にわずかに修正しました。

事実、最適化空間の次元が小さいほど（この場合は2に等しい）、子孫は「より近く」になります。遺伝的最適化アルゴリズムは、娘個人の遺伝子の「継承」のルールを厳密に決定しません。したがって、ランダムに、ニキータは何の変化もなしに彼の目の色を借りましたが、彼は両親のどちらか一方の近くにいることが判明しました。私の実装では、同じ成功を収めて、ニキータは両方の親から元のパラメーターを借りることができました。

第三段階は繁殖です

進化過程のムーバー、自然selection。 10人の最高の個人のうち4人がさらに10人の子を与えました。現在、20人の個人がいます。遺伝的最適化アルゴリズムには、一定の母集団サイズの維持が含まれます。 10人が「死ぬ」必要があります。この実装では、第1世代のほとんどの個人が80％から100％に「死ぬ」。

したがって、この例では、新世代は0〜2人の親と8〜10人の子孫で構成されます。言い換えると、歌詞を省略すると、トレーディングロボットのパラメーターの新しいベクトルは、前のステップで得られた4つのベストテストの「伝播」（組み合わせ）から計算されます。ほとんどの「高齢者」は、選択の新しい反復への参加を受け入れません（選択を実装するための他のオプションが可能です）。

アルゴリズムの完了

複製と選択はN回繰り返されます。具体的には、この例では、以前にテストされた3つのアルゴリズムと比較するために、10の個人の4世代、合計40のテストがテストされます。

しかし、別の人口が崩壊する可能性があります。つまり、すべてのテストはいくつかのポイントの近くにあります。この状況を回避するには、特にいくつかのメカニズムが使用されます。

人口への「新鮮な血液」の注入。現在の人口の子孫には、最初の人口が形成されたのと同じ方法で、偶然に得られたいくつかの新しい個人が追加されます。
突然変異メカニズム：個々の子孫は、その親の特性とわずかに異なるいくつかの特性（座標）を持っている場合があります。

この例では

子孫のジェーンとジョスの特徴-「成長」と「目の色」はそれぞれの親から借用され、
サムとシリの子孫の特性は、両方の親の個人の対応する特性とわずかに異なります。

私の実装では、突然変異と「新鮮な個人」にもかかわらず、限られたスペースでの集団全体の時期尚早な収束、ローカリゼーションを避けるために、集団を全体として定期的に更新する必要がありました。

モンテカルロアルゴリズム、勾配降下、および「海戦」という作業名のアルゴリズムをテストした元のデータに戻ると、最適化プロセスは次のアニメーションで示すことができます。

アニメーションからわかるように、最初はポイントの配置は混oticとしていますが、その後の世代では、DF値が高いエリアになりがちです。

同じ表面上のアルゴリズムを比較します： P = f（ M 、 T ）：

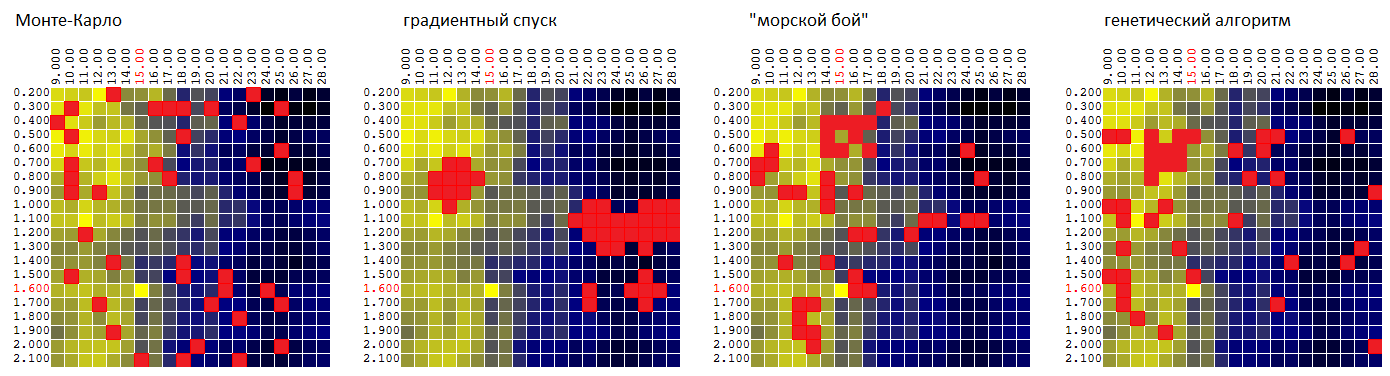
モンテカルロ	勾配降下	「海戦」	遺伝的アルゴリズム
95.7％	92.1％	97.0％	96.8％

グローバル値の割合として検出されたCFの極値の平均値。

もちろん、1組の入力データで判断するのは時期尚早ですが、これまでのところ、GAは、取引ロボットに関して、「海戦」アルゴリズムよりも劣っています。

まったく取るに足らない-見つかったCFの準最適値の平均で、
取引アルゴリズムのパラメトリック安定性の最悪の推定値を提供します。これは、詳細が少なすぎると見られる準最適なパラメータータプルの周囲を「調査」しないためです。

4つの最適化アルゴリズムの最終テスト

最終テストは、4セットの入力データ（価格履歴の4つの異なるセグメントでの取引戦略のバックテストの結果（ EURUSD ：2016、EURUSD：2017、 XAUUSD ：2016、XAUUSD：2017））で実行されました。

（価格の4つの時系列に対する2つのパラメーターの関数としてのデジタルフィルターの例）

今回は、3つのパラメーターに従って最適化が実行されました。

「高速」移動平均の期間
「遅い」移動平均の期間
TakeProfit（トランザクションが完了した時点でのトランザクションの利益（パーセント））。

各パラメーターは20の異なる値を取りました。テーブルを構築するための合計

P = F（Mf、Ms、T）

ここで、Pは利益、Mfは「速い」移動平均の期間、Msは「遅い」移動平均の期間、TはTakeProfit、

20 * 20 * 20 = 8,000回のテスト反復が実行されました。

160、400、および800のテスト（選択した座標でのDF計算）の制限で最適化が実行されました。毎回、1,000回の最適化反復の結果を平均しました。見つかったパラメーターの準最適ベクトルの平均DF値は次のとおりです。

モンテカルロ	勾配降下	「海戦」	遺伝的アルゴリズム
84.1％	83.9％	77.0％	92.6％

それとは別に、オプションの可能な合計数のわずかな割合のテストでも、GAが良い結果を示すことに注意する価値があります。

テスト	モンテカルロ	勾配降下	「海戦」	遺伝的アルゴリズム
8,000のうち160	79.1％	76.7％	73.1％	87.7％
8,000のうち400	84.7％	85.0％	77.4％	93.7％
8,000のうち800	88.6％	90.1％	80.4％	96.3％

結論の代わりに

私は、遺伝的最適化アルゴリズムが示した結果に多少驚きました。具体的には、このメソッドの「遺伝的パラダイム」がリストの最初の場所を提供したとは思いません。ある意味で、座標の選択の論理によれば、それは二分法/黄金比の方法に似ていました。これらのアルゴリズムのいずれかを試して、GAと比較する価値があるでしょう。

トレーディングロボットに戻って、CF（利益）によって形成される表面の「レリーフ」が年々どのように変化するかに注目する価値があります。つまり、2017年の履歴でロボットを「最適化」することにより、これらの設定を2018年 （第1四半期、月、週... 2018年） に適用しても意味がありません 。

私たちのような人工、独断的で無力な取引戦略（移動平均の交差点で購入する）は、おそらくすぐに流行しません。残念ながら、他の戦略はありませんでした。したがって、取引ロボットの損益は、アルゴリズムの長所/短所ではなく運に起因すると考えています。したがって、トレーディングロボットのパラメトリック最適化のタスクは、個人的には専ら学術的関心のあるものです。

取引ロボットの最適化：遺伝的アルゴリズム