機械学習アルゴリズムの参照ベクトル法（SVM）の概要

まえがき

この記事では、SVMのいくつかの側面を検討します。

• SVMの理論的コンポーネント。
• クラスに線形に分割できないサンプルでアルゴリズムがどのように機能するか。
• SciKit LearnライブラリでのPythonの使用例とアルゴリズムの実装。

次の記事では、このアルゴリズムの数学的コンポーネントについて説明します。



ご存じのとおり、機械学習タスクは、分類と回帰という2つの主要なカテゴリに分類されます。 これらのタスクのどれに直面しており、このタスクにどのデータセットを持っているかに応じて、使用するアルゴリズムを選択します。



サポートベクターマシンメソッドまたはSVM（英語のサポートベクターマシンから）は、分類および回帰の問題で使用される線形アルゴリズムです。 このアルゴリズムは実際に広く使用されており、線形および非線形の両方の問題を解決できます。 サポートベクターの「マシン」の本質は簡単です。アルゴリズムは、データをクラスに分割する線または超平面を作成します。

理論

アルゴリズムの主なタスクは、データを2つのクラスに分割する最も正確な線または超平面を見つけることです。 SVMは、入力でデータを受け取り、そのような分割線を返すアルゴリズムです。



次の例を考えてみましょう。 データセットがあり、赤い正方形を青い円から分類して分離したいとします（正と負を考えましょう）。 このタスクの主な目標は、これら2つのクラスを分離する「理想的な」行を見つけることです。







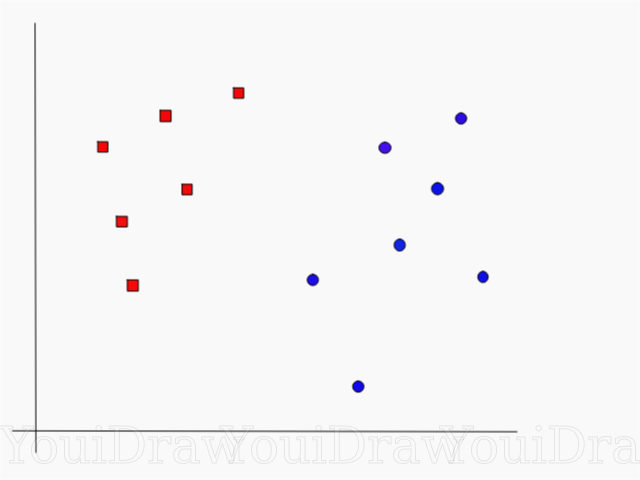
データセットを青と赤のクラスに分割する完全な線、つまり超平面を見つけます。



一見、それほど難しくないでしょう？



しかし、あなたが見ることができるように、そのような問題を解決するだれも、ユニークな行がありません。 これら2つのクラスを分離できる無限の行を選択できます。 SVMはどのように「理想的な」ラインを正確に見つけ、その理解において「理想的な」ものとは何か



以下の例を見て、2つのクラス（黄色または緑）のどちらが2つのクラスを最もよく分離し、「理想」の説明に適合するかを考えてください。







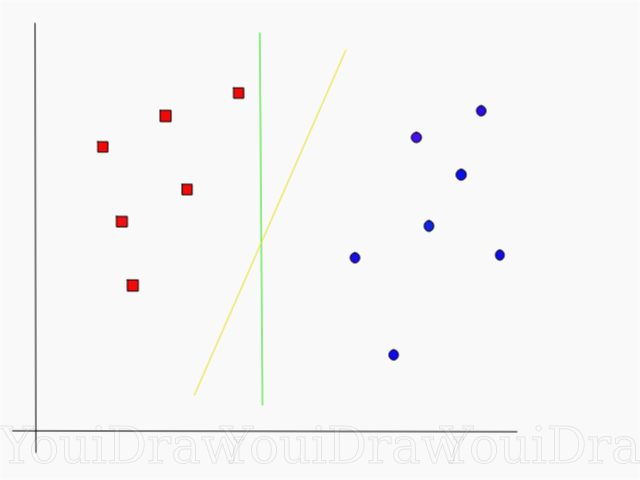
あなたの意見では、どの行がデータセットをよりよく分離していますか？



黄色の線を選択した場合、私はあなたを祝福します。これはアルゴリズムが選択する線です。 この例では、黄色の線が分離し、それに応じて2つのクラスが緑よりも適切に分類されることを直感的に理解できます。



緑の線の場合-赤のクラスに近すぎます。 彼女は現在のデータセットのすべてのオブジェクトを正しく分類したという事実にもかかわらず、そのような行は一般化されません-なじみのないデータセットと同じように動作しません。 2つのクラスを分離する一般化されたクラスを見つけるタスクは、機械学習の主なタスクの1つです。

SVMが最適なラインを見つける方法

SVMアルゴリズムは、最も近い分離線に直接位置するグラフ上のポイントを検索するように設計されています。 これらのポイントはサポートベクターと呼ばれます。 次に、アルゴリズムはサポートベクトルと分割面の間の距離を計算します。 これはギャップと呼ばれる距離です。 アルゴリズムの主な目標は、クリアランス距離を最大化することです。 最適な超平面は、このギャップが可能な限り大きい超平面であると見なされます。







かなり簡単ですね。 線形に分割できないより複雑なデータセットを使用した次の例を検討してください。







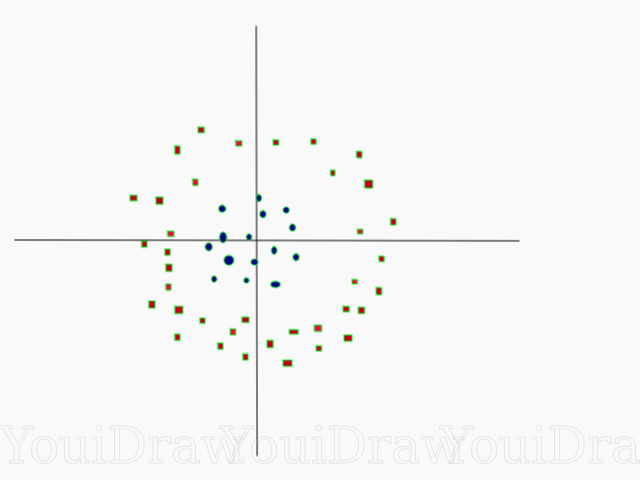
明らかに、このデータセットは線形に分割できません。 このデータを分類する直線を描くことはできません。 ただし、このデータセットは、Z軸と呼ばれる追加の次元を追加して線形に分割することができます。Z軸上の座標は、次の制限によって規制されていると想像してください

$$

$$z =x²+y²$$

したがって、縦座標Zは、ポイントの距離の2乗から軸の始点までを表します。

以下は、Z軸上の同じデータセットの視覚化です。







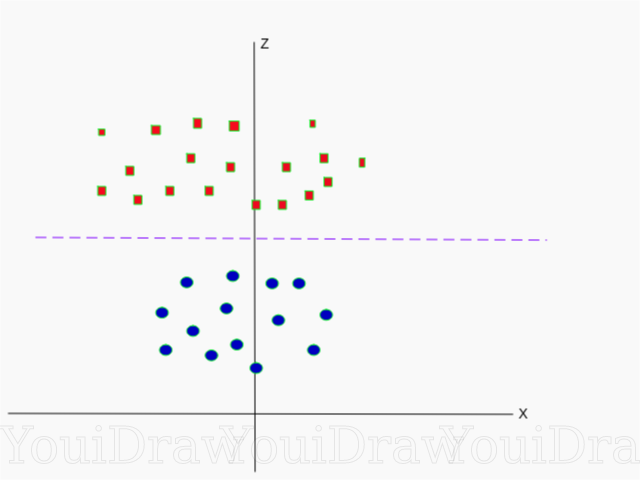
これで、データを線形に分割できます。 データz = kを分離するマゼンタの線であるとします。ここで、kは定数です。 もし

$$

$$z =x²+y²$$

それから

$$

$$k =x²+y²$$

-サークル式。 したがって、この変換を使用して、線形ディバイダーを元のサンプル次元数に戻すことができます。







その結果、追加のディメンションを追加することで非線形データセットを分類し、数学的な変換を使用して元の形式に戻すことができます。 ただし、すべてのデータセットでは、このような変換を簡単に開始することはできません。 幸いなことに、このアルゴリズムをsklearnライブラリに実装すると、この問題が解決されます。

ハイパープレーン

アルゴリズムのロジックに慣れてきたので、超平面の正式な定義に進みます



超平面は、空間を2つの別々の部分に分割するn次元ユークリッド空間内のn-1次元の部分平面です。



たとえば、ラインが1次元のユークリッド空間として表されている（つまり、データセットが直線上にある）と想像してください。 この線上の点を選択します。 この時点で、データセット（この場合は行）を2つの部分に分割します。 ラインには1つのメジャーがあり、ポイントには0メジャーがあります。 したがって、点は線の超平面です。



先に出会った2次元データセットの場合、分割線は同じ超平面でした。 簡単に言えば、n次元の空間には、この空間を2つの部分に分割するn-1次元の超平面があります。



コード

import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ポイントはXの配列として表され、それらが属するクラスはyの配列として表されます。

次に、このサンプルを使用してモデルをトレーニングします。 この例では、「コア」分類子（カーネル）の線形パラメーターを設定します。

 from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

新しいオブジェクトのクラス予測

 prediction = clf.predict([[0,6]])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

パラメータ設定

パラメーターは、分類子を作成するときに渡す引数です。 以下に、最も重要なカスタムSVM設定の一部を示します。



「C」



このパラメーターは、「滑らかさ」とトレーニングサンプル内のオブジェクトの分類の精度との間の細かな線を調整するのに役立ちます。 「C」値が高いほど、より多くのトレーニングサンプルオブジェクトが正しく分類されます。







この例では、この特定のサンプルに対して定義できるいくつかの決定しきい値があります。 直接（チャートに緑色の線として表示）決定のしきい値に注意してください。 これは非常に単純であり、このため、いくつかのオブジェクトが誤って分類されました。 誤って分類されたこれらのポイントは、データでは外れ値と呼ばれます。



また、最終的により曲線（水色の決定しきい値）が得られるようにパラメーターを調整することもできます。これにより、すべてのトレーニングサンプルデータが正しく分類されます。 もちろん、この場合、新しいデータでモデルが一般化して同等の良好な結果を示すことができる可能性は、壊滅的に小さいです。 したがって、モデルをトレーニングするときに精度を達成しようとしている場合は、より直接的に、より均一な何かを目指してください。 「C」の値が大きいほど、モデル内で超平面が絡み合いますが、トレーニングセット内の正しく分類されたオブジェクトの数が多くなります。 したがって、再トレーニングを回避すると同時に高い精度を達成するために、特定のデータセットのモデルパラメーターを「ねじる」ことが重要です。



ガンマ



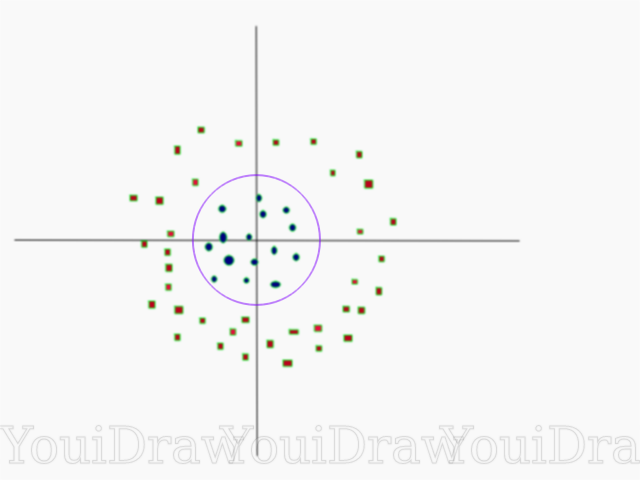
公式文書では、SciKit Learnライブラリは、ガンマがデータセット内の各要素が「理想的なライン」の決定に影響を与える程度を決定すると述べています。 ガンマが低いほど、分割線から十分に離れた要素であっても、より多くの要素がこのまさにラインを選択するプロセスに参加します。 ガンマが高い場合、アルゴリズムは、線自体に最も近い要素にのみ「依存」します。

ガンマレベルの設定が高すぎる場合、線に最も近い要素のみが線の位置に関する意思決定プロセスに参加します。 これは、データ内の外れ値を無視するのに役立ちます。 SVMアルゴリズムは、決定を行う際に、互いに最も近くにあるポイントの重みが大きくなるように設計されています。 ただし、「C」と「ガンマ」を正しく設定すると、最適な結果を得ることができ、外れ値を無視してより線形の超平面が構築され、したがってより一般化できます。

おわりに

この記事が、SVMまたはReference Vector Methodの仕事の本質を理解するのに役立つことを心から願っています。 コメントやアドバイスをお待ちしています。 以降の出版物では、SVMの数学的要素と最適化の問題について説明します。



ソース：

SciKit Learnの公式SVMドキュメント

TowardsDataScienceブログ

Siraj Raval：サポートベクターマシン

機械学習Udacity SVMの概要：ガンマコースビデオ

ウィキペディア：SVM