
私たちは非常に若いが、信じられないほど美しく、強力なプログラミング言語Juliaと知り合いです。 6年間のベータ版がついに終了したため、構文の変更を恐れることはできません。 そして、誰もが1つからインデックスを作成するのが良いか悪いかを議論している間、興奮したコミュニティは積極的に混乱しています:新しいライブラリが出てきて、古いライブラリが更新され、深刻なプロジェクトが始まり、学生は大学でこの言語を積極的に教えています。 取り残されないようにしましょう! 今晩コーディングするので、お茶を強くします!
仕事の準備
ここにはロシア語の小さなレビューがあり、ハブにも言語とインストール手順に関する知識があります 。 繰り返しますが、 Windows Management Frameworkの必要性に焦点を当てます。そうしないと、パッケージのダウンロードに問題が発生します。
アップグレード後、 JuliaPROにはJunoのみが含まれるようになりました。 しかし、私は個人的にJupyterがより好きです 。ラップトップでは問題ありませんでした。さらに 、ブラウザーで作業し、すぐにメモや数式を作成すると便利です。一般に、レポート、スライド、またはマニュアルの作成に最適です。
Juliaにはいくつかのパッケージがありますが、最も成功したものはバックエンドとしてPlotsに含まれています。 Plots.jl
メタ言語:つまり、さまざまなチャート作成ライブラリのインターフェース。 したがって、 Plots.jl
実際にはコマンドを解釈してから、ある種のグラフライブラリを使用してグラフを作成します。 これらのバックグラウンドグラフィックライブラリはバックエンドと呼ばれます。 最良の部分は、多くの異なるグラフィックライブラリをPlots.jl
構文で使用できることです。また、 Plots.jl
がこれらの各ライブラリに新しい機能を追加することもわかります。
パッケージをインストールするには、REPL、Juno、またはJupyterでコマンドを実行します。
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
すべてのパッケージをインストールする必要はありませんが、各パッケージには独自の特性があることを知っておく必要があります。 私はplotlyjs()を好みます :速度には違いはありませんが、非常にインタラクティブです。 ファイルを保存する機能と同様に、平面に沿って移動するズームがあり、 Jupyterドキュメントをhtmlとして保存すると、すべての機能が保存されます。 そのため、サイトに追加したり、インタラクティブなプレゼンテーションを作成したりできます。 ページの詳細: プロット 、 Gadfly
無限の素数パターン
Habrに関する記事のアイデアを実装しました 。 簡単に言うと、ポイントの座標を取得し、横座標と縦座標の間の演算(XORまたはビット単位ANDなど)を使用し、単純化またはフィボナッチ数に属しているかどうかを確認し、答えが「はい」の場合、ポイントを1色で塗りつぶします。そして、別のネガで? チェック:
using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
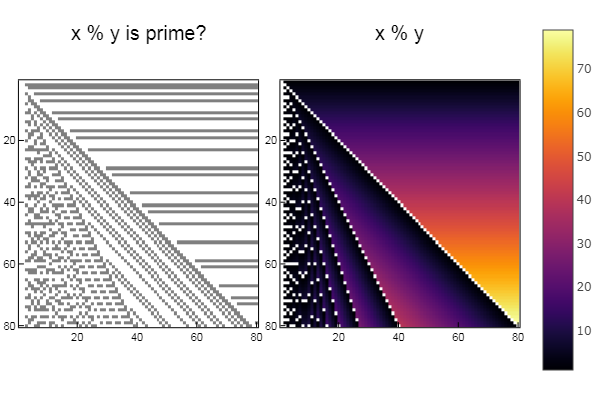
W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
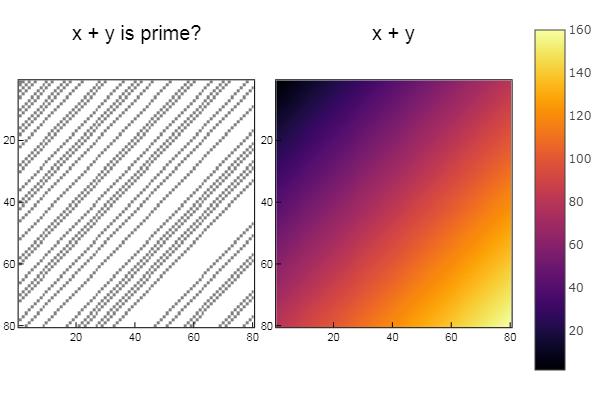
W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
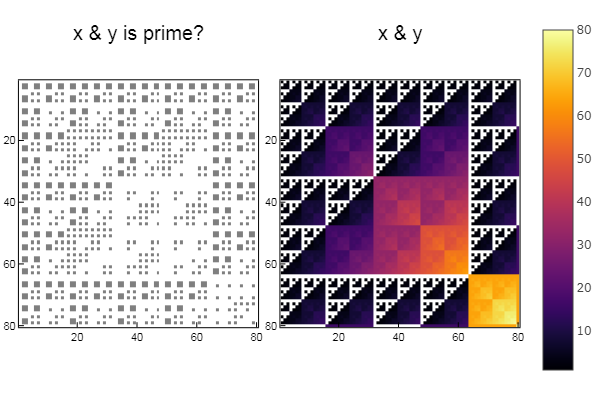
W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
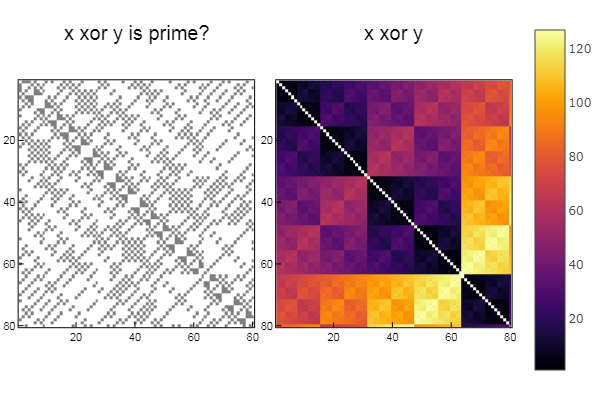
次のようなものを使用して、通常どおりシリーズを作成できます。
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
しかし、マトリックス表現を使用してみましょう( 詳細 )。
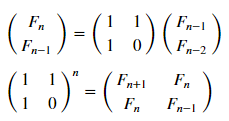
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
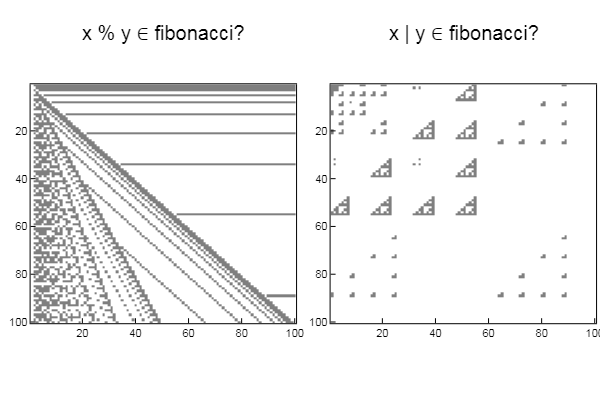
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
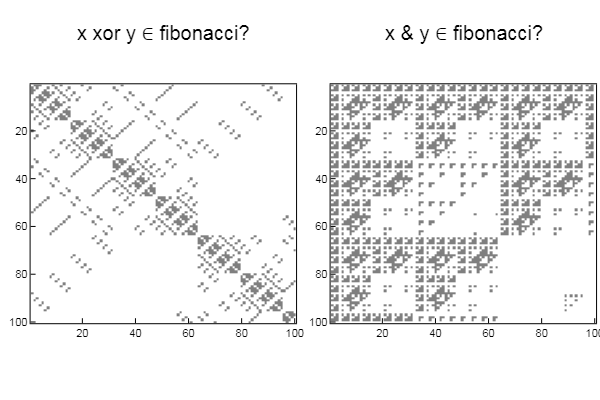
比較的まっすぐな人物の反射
このタイプの表示は、マトリックスによって決定されます。
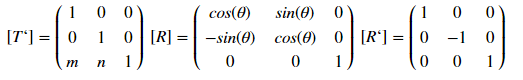
ここで、[T ']、[R]、および[R']は、それぞれ変位、回転、反射マトリックスです。 どのように機能しますか? オフセットの例を調べてみましょう-座標(x、y)を持つポイントの場合、mによるxによるオフセットとゲームによるnによるオフセットは、変換によって決定されます。
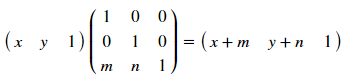
これらのマトリックスにより、さまざまなポリゴンの変換が可能になります。主なことは、座標を互いの下に記録し、最後に単位列を忘れないことです。 したがって、[T]:
- 変換されるポリゴンとともに原点の線をシフトします
- X軸と一致するように回転します
- Xに関して多角形のすべての点を反映します
- 逆転とキャリーが続きます
このトピックの詳細については、 Rogers D.、Adams J.のコンピューターグラフィックスの数学的基礎を参照してください。
今すぐコーディングしましょう!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
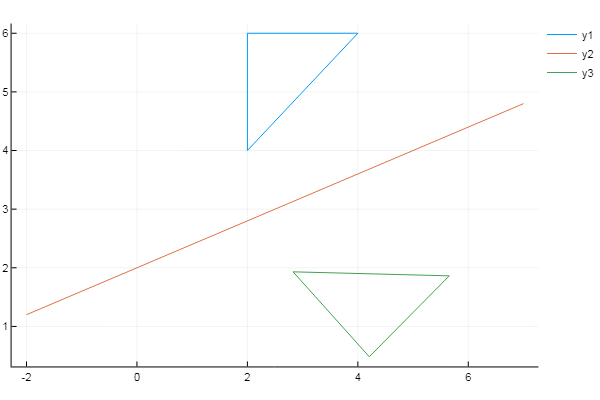
興味深い事実:ギリシャ文字を取り除き、最初の行を
function y=f(x,t) y=0.4*x + 2 endfunction,
角括弧[]は()上の配列のインデックスとplot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) )
上のラフトplot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) )
ため、このコードはScilabでほとんど実行されます。
三次元グラフィックスを使用する
これらのパッケージの一部は、3次元グラフの構築をサポートしています。 しかし、 juliaで OpenGL機能を実装するGLFWおよびGLAbstractionパッケージと連携して動作するMakieのかなり強力な視覚化ツールについても言及したいと思います。 Makieに関する詳細情報。 彼の承認を非表示にします
using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
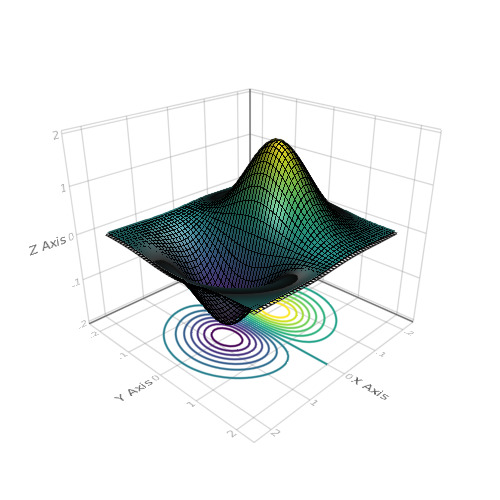
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
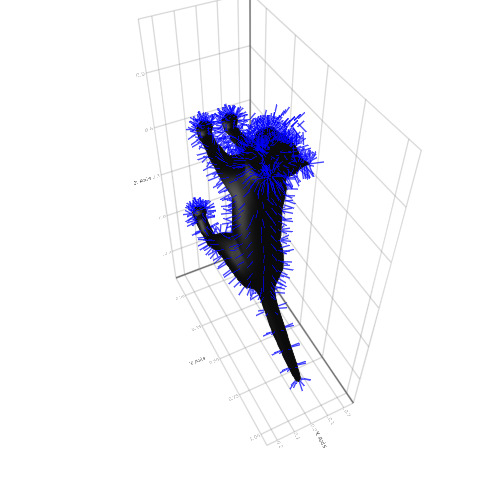
それはすべてグラフィックスです。 インタラクティブ性、アニメーション、3D、ビッグデータ、またはシンプルなグラフの高速構築-常に進化するパッケージは、ほぼすべての好みとニーズを満たすだけでなく、すべてが非常に簡単に習得できます。 実践的な演習をダウンロードして、ジュリアを理解し続けてください!
UPD:上記のすべてのリストは、julia 0.6.4を使用してJupyterで作成されています。 残念ながら、Plotsメタパッケージの一部の機能は削除または名前変更されたため、更新を監視し続けていますが、今のところスパイは完全に置き換えられています。
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)