
シンボリック計算を使用したPythonでのアルゴリズムの実装は、微分方程式で定義されたオブジェクトの数学的モデリングの問題を解決するのに非常に便利です。 このような方程式を解くには、ラプラス変換が広く使用されます。これにより、簡単に言えば、問題を単純な代数方程式を解くことに減らすことができます。
この出版物では、SymPyライブラリの直接および逆ラプラス変換の関数を検討することを提案します。これにより、Pythonを使用して微分方程式やシステムを解くためにラプラス法を使用できます。
ラプラス法自体と、線形微分方程式や線形システムを解く際のその利点は、たとえば、人気のある出版物[1]などの文献で広く取り上げられています。 本では、ラプラス法は、著者が選択した例を使用して、ライセンスソフトウェアパッケージMathematica、Maple、およびMATLAB(教育機関によるこのソフトウェアの購入を意味します)での実装について提示されています。
今日は、Pythonを使用して学習問題を解決する別の例ではなく、直接および逆ラプラス変換の機能を使用して線形微分方程式およびシステムを解決する一般的な方法を検討してみましょう。 同時に、学習の時間を節約します:コーシー条件を含む線形微分方程式の左側は、学生自身によって形成され、方程式の右側の直接ラプラス変換で構成されるタスクのルーチン部分は、 laplace_transform()関数を使用して実行されます。
ラプラスの原作者の物語が変わる
ラプラス変換(ラプラス画像)には興味深い歴史があります。 ラプラス変換の定義における積分は、L。オイラーの著作の1つに初めて登場しました。 ただし、数学では、方法論または定理をオイラーの後に発見した数学者の名前と呼ぶことが一般に受け入れられています。 そうでなければ、数百の異なるオイラー定理があります。
この場合、オイラーの次はフランスの数学者ピエール・シモン・ド・ラプラス(ピエール・シモン・ド・ラプラス(1749-1827))でした。 確率論の研究でそのような積分を使用したのは彼でした。 ラプラス自身は、ラプラス変換(ラプラス画像)に基づく微分方程式の解を見つけるために、いわゆる「操作方法」を適用しませんでした。 これらの方法は実際に実用的なエンジニア、特に英国の電気技師のオリバー・ヘヴィサイド(1850-1925)によって発見され普及しました。 これらの方法の有効性が厳密に証明されるずっと前に、20世紀初頭でもその正当性は大いに疑問視されていましたが、この問題については非常に激しい議論がありましたが、演算法は成功裏に広く使用されました。
直接および逆ラプラス変換の機能
- ラプラス直接変換関数:
sympy.integrals.transforms。 laplace_transform (t、s、**ヒント)。
laplace_transform()関数は、実変数の関数f(t)から複素変数の関数F(s)へのラプラス変換を実行します。
F ( S ) = I N T ∞ 0 F ( T )E - S T D 、T 。
この関数は(F、a、cond)を返します。ここで、 F(s)は関数f(t)のラプラス変換、 a <Re(s)はF(s)が定義された半平面、 condは積分の収束の補助条件です。
積分を閉形式で計算できない場合、この関数は未計算のLaplaceTransformオブジェクトを返します。
オプションnoconds = Trueを設定すると、関数はF(s)のみを返します。 - 逆ラプラス変換関数:
sympy.integrals.transforms。 inverse_laplace_transform (F、s、t、plane = None、**ヒント)。
inverse_laplace_transform()関数は、複素変数F(s)の関数を実変数の関数f(t)に逆ラプラス変換します。
f(t)= frac12 pii intc+∞ cdotic−∞ cdotiestF(s)ds。
積分を閉じた形で計算できない場合、この関数はオブジェクトの呼び出されていないInverseLaplaceTransformを返します。
レギュレーターの遷移特性を決定する例の逆ラプラス変換
PIDコントローラーの伝達関数の形式は[2]です。
W(s)=(1+ fracKd cdotTd cdots1+Td cdots) cdotKp cdot(1+ frac1Ti cdots) c d o t f r a c 1 s
PIDおよびPIコントローラーの過渡特性の方程式を取得して、伝達関数を縮小し、さらに逆視覚ラプラス変換にかかる時間を導出するプログラムを作成します。
# : from sympy import * import time import matplotlib.pyplot as plt import numpy as np start = time.time() # : var('s Kp Ti Kd Td') # : var('t', positive=True) Kp = 2 Ti = 2 Kd = 4 Td = Rational(1, 2) # - s: fp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) # -, # : ht = inverse_laplace_transform(fp, s, t) Kd = 0 # - (Kd = 0) s: fpp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) # -, # : htt = inverse_laplace_transform(fpp, s, t) stop = time.time() print (' : %ss' % N((stop-start), 3)) # : f = lambdify(t, ht, 'numpy') F = lambdify(t, htt, 'numpy') tt = np.arange(0.01, 20, 0.05) # : plt.title(' \n : \n - W(s)=%s \n - W(s)=%s' % (fp, fpp)) plt.plot(tt, f(tt), color='r', linewidth=2, label='-: h(t)=%s' % ht) plt.plot(tt, F(tt), color='b', linewidth=2, label='-: h(t)=%s' % htt) plt.grid(True) plt.legend(loc='best') plt.show()
取得するもの:
逆視覚ラプラス変換時間:2.68秒
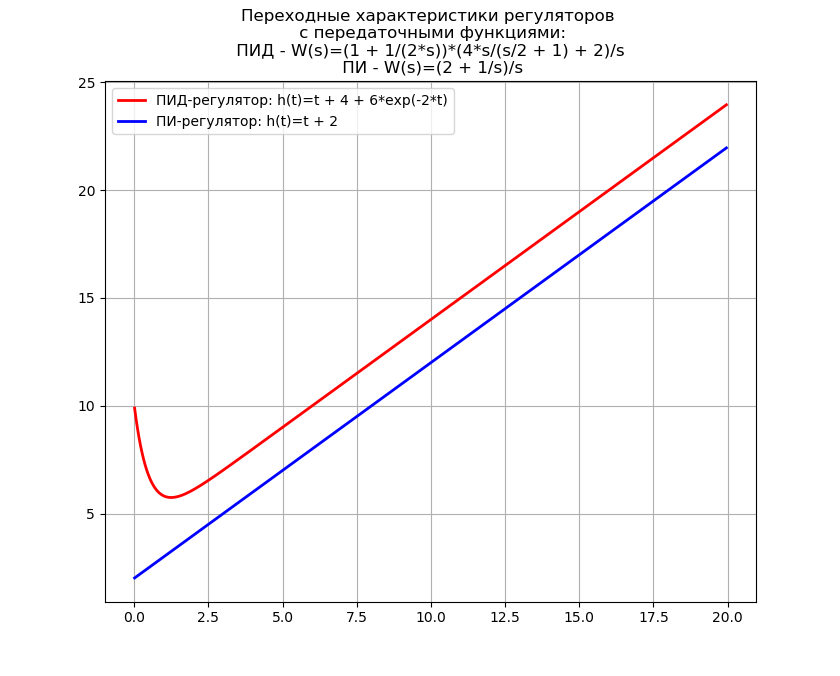
逆ラプラス変換は、PythonがMathCADのような高価なソフトウェア「モンスター」を置き換えることができる自走式銃の合成でよく使用されるため、上記の逆変換の使用は実用的に重要です。
コーシー問題を解くための高次の導関数からのラプラス変換
議論の続きでは、ラプラス変換(ラプラス画像)を、次の形式の定数係数を持つ線形微分方程式の解の探索に適用します。
a cdotx″(t)+b cdotx′(t)+c cdotx(t)=f(t)(1)
aとbが定数の場合、
L \左\ {a \ cdot f(t)+ b \ cdot q(t)\右\} = a \ cdot L \左\ {f(t)\右\} + b \ cdot L \左\ {q(t)\右\}(2)
関数f(t)とq(t)の両方のラプラス変換(ラプラス画像)が存在するようなすべてのsに対して。
以前に検討された関数laplace_transform()およびinverse_laplace_transform()を使用して、直接および逆ラプラス変換の線形性を検証しましょう。 このために、 f(t)= sin(3t) 、 q(t)= cos(7t) 、 a = 5 、 b = 7を例にとり、次のプログラムを使用します。
from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t) # a*L{f(t)}: L1 = a * laplace_transform(f, t, s, noconds=True) # b*L{q(t)}: L2 = b*laplace_transform(q, t, s, noconds=True) # a*L{f(t)}+b*L{q(t)}: L = factor(L1 + L2) print (L) # L{a*f(t)+b*q(t)}: LS = factor(laplace_transform(a*f + b*q, t, s, noconds=True)) print (LS) print (LS == L) # a* L^-1{f(t)}: L_1 = a * inverse_laplace_transform(L1/a, s, t) # b* L^-1{q(t)} L_2 = b * inverse_laplace_transform(L2/b, s, t) # a* L^-1{f(t)}+b* L^-1{q(t)}: L_S = L_1 + L_2 print (L_S) # L^-1{a*f(t)+b*q(t)}: L_1_2 = inverse_laplace_transform(L1 + L2, s, t) print (L_1_2) print (L_1_2 == L_S)
取得するもの:
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735)/((s ** 2 + 9)*(s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735)/((s ** 2 + 9)*(s ** 2 + 49))
本当
5 * sin(3 * t)+ 7 * cos(7 * t)
5 * sin(3 * t)+ 7 * cos(7 * t)
上記のコードは、逆ラプラス変換の一意性も示しています。
と仮定して q(t)=f′(t) 最初の定理の条件を満たし、この定理から次のようになります。
L \左\ {f ''(t)\右\} = L \左\ {q '(t)\右\} = sL \左\ {q(t)\右\}-q(0) = sL \ left \ {f '(t)\ right \}-f'(0)= s \ left [sL \ left \ {f(t)-f(0)\ right \} \ right]、
したがって、
L \左\ {f ''(t)\右\} = s ^ {2} \ cdot F(s)-s \ cdot f(0)-f '(0)。
この計算を繰り返すと、
L \左\ {f '' '(t)\右\} = sL \左\ {f' '(t)\右\}-f' '(0)= s ^ {3} F(s) -s ^ {2} f(0)-sf '(0)-f' '(0)。
そのようなステップの有限数の後、最初の定理の次の一般化を取得します。
L \左\ {f ^ {(n)}(t)\右\} = s ^ {n} L \左\ {f(t)\右\}-s ^ {n-1} f(0 )-s ^ {n-2} f '(0)-\ cdot \ cdot \ cdot -f ^ {(n-1)}(0)=
=snF(s)−sn−1f(0)− cdot cdot cdot−sf(n−2)(0)−f(n−1)(0)。(3)
初期条件をもつラプラス変換された目的関数の導関数を含む関係(3)を式(1)に適用すると、SymPyライブラリーのScorobeyの積極的なサポートにより、当部門で特別に開発された方法に従ってその解を得ることができます。
SymPyライブラリを使用して、ラプラス変換に基づく線形微分方程式および連立方程式を解く方法
この方法を実証するために、外力が加えられるバネに取り付けられた、特定の質量の質点で構成されるシステムの運動を記述する単純な微分方程式を使用します。 このようなシステムの微分方程式と初期条件の形式は次のとおりです。
x″+4x= sin(3t);x(0)=1.2;x′(0)=1、(4)
どこで x(0) -質量の初期位置の減少、 x′(0) -初期質量速度の低下。
ゼロ以外の初期条件で方程式(4)によって定義される単純化された物理モデル[1]
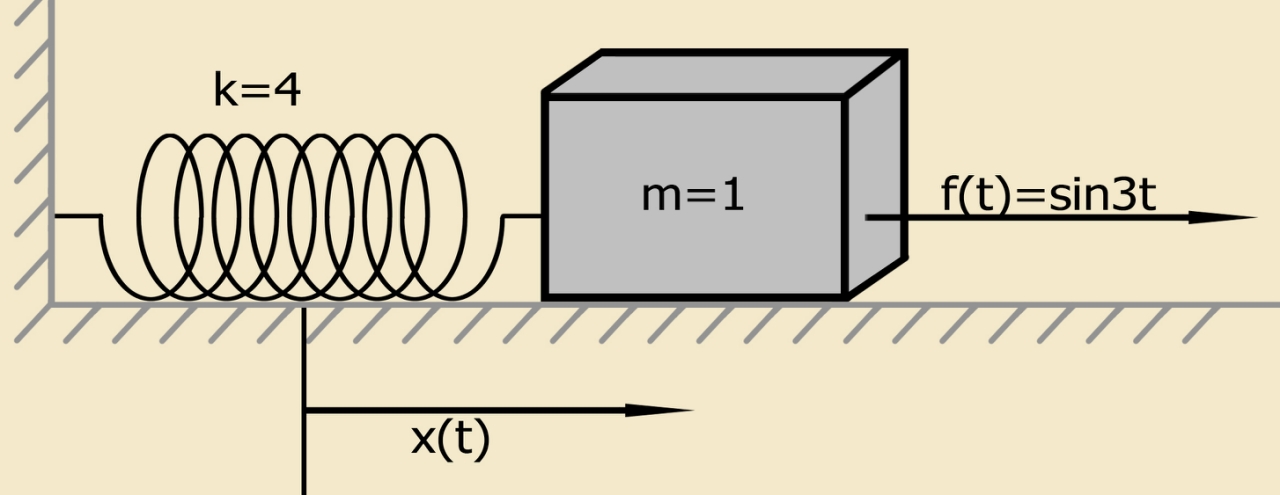
バネ上に固定された所定の質量の質点で構成されるシステムは、コーシー問題(初期条件の問題)を満たします。 与えられた質量の質点は、最初は平衡位置で静止しています。
これと他の線形微分方程式をラプラス変換法で解くには、関係式(3)から得られる次のシステムを使用すると便利です。
L \左\ {f ^ {IV}(t)\右\} = s ^ {4} \ cdot F(s)-s ^ {3} \ cdot f(0)-s ^ {2} \ cdot f ^ {I}(0)-s \ cdot f ^ {II}(0)-f ^ {III}(0)、
L \左\ {f ^ {III}(t)\右\} = s ^ {3} \ cdot f(s)-s ^ {2} \ cdot f(0)-s \ cdot f ^ {I }(0)-f ^ {II}(0)、
L \左\ {f ^ {II}(t)\右\} = s ^ {2} \ cdot F(s)-s \ cdot f(0)-f ^ {I}(0)、
L \左\ {f ^ {I}(t)\右\} = s \ cdot F(s)-f(0)、L \左\ {f(t)\右\} = F(s) 。
L \左\ {f(t)\右\} = F(s)。 (5)
SymPyを使用したソリューションのシーケンスは次のとおりです。
- 必要なモジュールをロードし、シンボリック変数を明示的に定義します:
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
- sympyライブラリのバージョンを指定して、その機能を考慮します。 これを行うには、次の行を入力します。
import SymPy print (' sympy – %' % (sympy._version_))
- 問題の物理的な意味に従って、時間変数はゼロと正の数を含む領域に対して決定されます。 式(4)の右辺に初期条件と関数を設定し、その後のラプラス変換を行います。 10進数の丸めを使用するとエラーが発生するため、初期条件にはRational関数を使用する必要があります。
# : x0 = Rational(6, 5) # : x01 = Rational(1, 1) g = sin(3*t) Lg = laplace_transform(g, t, s, noconds=True)
- (5)を使用して、式(4)の左辺に含まれるラプラス変換された導関数を書き換え、それらからこの式の左辺を形成し、結果をその右辺と比較します。
d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg)
- 得られた変換X(s)の代数方程式を解き、逆ラプラス変換を実行します。
rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t)
- SymPyライブラリの作業からNumPyライブラリに移行します。
f = lambdify(t, soln, 'numpy')
- 通常のPythonメソッドをプロットします。
x = np.linspace(0, 6*np.pi, 100) plt.title(', \n :\n (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print (" sympy – %s" % (sympy.__version__)) # : x0 = Rational(6, 5) # : x01 = Rational(1, 1) g = sin(3*t) # : Lg = laplace_transform(g, t, s, noconds=True) d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) # : rez = solve(de, X(s))[0] # : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(', \n :\n (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
取得するもの:
Sympyライブラリバージョン-1.3
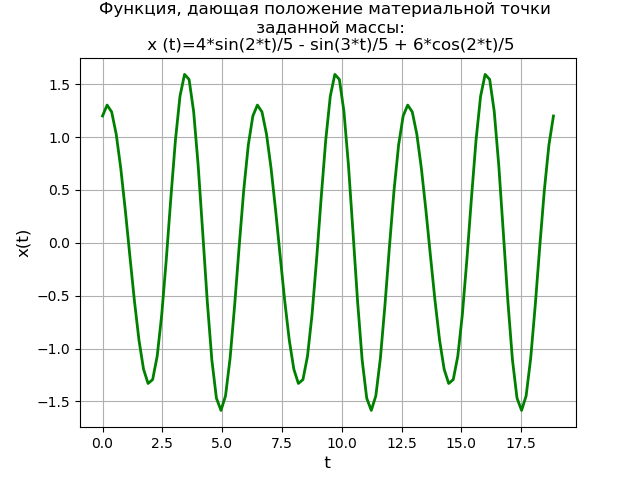
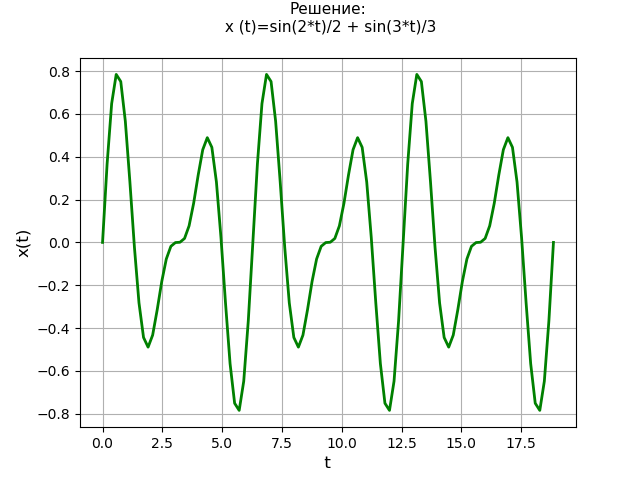
与えられた質量の質点の位置を与える周期関数のグラフが取得されます。 SymPyライブラリを使用したラプラス変換方法は、最初に同次方程式の一般的な解と初期の異種微分方程式の特定の解を見つける必要がないだけでなく、基本分数法とラプラステーブルを使用する必要もない解決策を提供します。
同時に、システム(5)を使用し、NumPyにアクセスしてより生産的な方法を使用してソリューションを研究する必要があるため、ソリューションメソッドの教育的価値は維持されます。
この方法をさらに実証するために、微分方程式系を解きます。
begincases2x″+6x−2=0、y″−2x+2y=40 cdot sin(3t)、 endcases(6)
初期条件で x(0)=y(0)=y′(0)=0
初期条件がゼロの場合の連立方程式(6)によって定義される単純化された物理モデル:

したがって、力f(t)は 、システムがその平衡位置で静止しているときに、時間t = 0で所定の質量の2番目の物質点に突然加えられます。
連立方程式の解は、以前に考えられていた微分方程式(4)の解と同じです。したがって、説明なしでプログラムテキストを引用します。
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
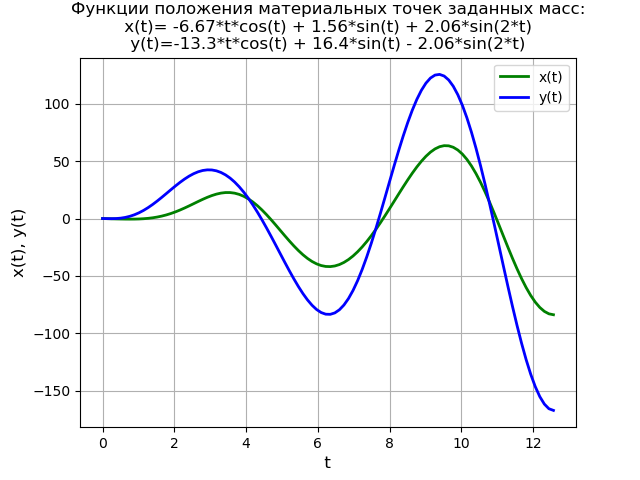
取得するもの:
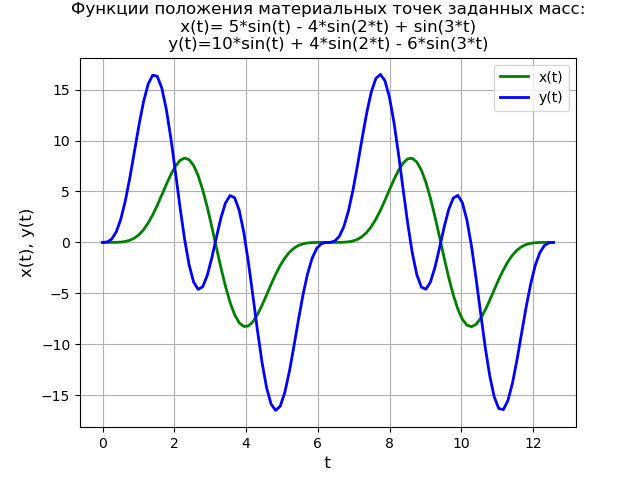
非ゼロの初期条件の場合、プログラムテキストと関数グラフは次の形式を取ります。
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
初期条件がゼロの4次線形微分方程式の解を考えてみましょう。
x(4)+2 cdotx″+x=4 cdott cdotet;
x(0)=x′(0)=x″(0)=x(3)(0)=0
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) # : x0 = 0 x01 = 0 x02 = 0 x03 = 0 g = 4*t*exp(t) # : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 2*d2 + d0) de = Eq(d, Lg) # : rez = solve(de, X(s))[0] # : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
決定スケジュール:

4次の線形微分方程式を解きます。
x(4)+13x″+36x=0;
初期条件で x(0)=x″(0)=0 、 x′(0)=2 、 x(3)(0)=−13 。
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) # : x0 = 0 x01 = 2 x02 = 0 x03 = -13 d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 13*d2 + 36*d0) de = Eq(d, 0) # : rez = solve(de, X(s))[0] # : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
決定スケジュール:
ODEを解くための関数
分析ODEソリューションおよびODEシステムを使用している場合、 dsolve()関数が使用されます。
sympy.solvers.ode。 dsolve (eq、func = None、hint = 'default'、simplify = True、ics = None、xi = None、eta = None、x0 = 0、n = 6、** kwargs)
dsolve()関数のパフォーマンスをLaplaceメソッドと比較してみましょう。 たとえば、初期条件がゼロの次の4次微分方程式を考えます。
x(IV)(t)=3 cdotx‴(t)−x(t)=4 cdott cdot exp(t);
x(0)=x′(0)=x″(0)=x‴(0)=0
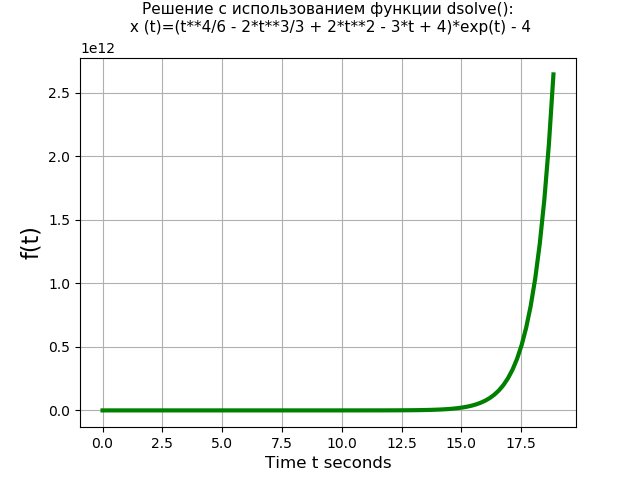
from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t) # : de = Eq(u.diff(t, t, t, t) - 3*u.diff(t, t, t) + 3*u.diff(t, t) - u.diff(t), 4*t*exp(t)) # : des = dsolve(de, u) # : eq1 = des.rhs.subs(t, 0) eq2 = des.rhs.diff(t).subs(t, 0) eq3 = des.rhs.diff(t, t).subs(t, 0) eq4 = des.rhs.diff(t, t, t).subs(t, 0) # : seq = solve([eq1, eq2-1, eq3-2, eq4-3], C1, C2, C3, C4) rez = des.rhs.subs([(C1, seq[C1]), (C2, seq[C2]), (C3, seq[C3]), (C4, seq[C4])]) def F(t): return rez f = lambdify(t, rez, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print (' dsolve(): %ss' % round((stop-start), 3)) plt.title(' dsolve():\n (t)=%s\n' % rez, fontsize=11) plt.grid(True) plt.xlabel('Time t seconds', fontsize=12) plt.ylabel('f(t)', fontsize=16) plt.plot(x, f(x), color='#008000', linewidth=3) plt.show()
取得するもの:
dsolve()関数を使用した方程式の時間:1.437 s
from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function) # : x0 = 0 x01 = 0 x02 = 0 x03 = 0 # : g = 4*t*exp(t) # : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d3 = s**3*X(s) - s**2*x0 - s*x01 - x02 d2 = s**2*X(s) - s*x0 - x01 d1 = s*X(s) - x0 d0 = X(s) # : d = factor(d4 - 3*d3 + 3*d2 - d1) de = Eq(d, Lg) # : rez = solve(de, X(s))[0] # : soln = collect(inverse_laplace_transform(rez, s, t), t) f = lambdify(t, soln, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print (' : %ss' % round((stop-start), 3)) plt.title(' :\n (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
取得するもの:
ラプラス変換を使用した方程式の時間:3.274 s

したがって、dsolve()関数(1.437 s)は、ラプラス変換法(3.274 s)で2回以上解くよりも高速に4次方程式を解きます。 ただし、dsolve()関数は2階微分方程式を解かないことに注意してください。たとえば、dsolve()関数を使用してシステム(6)を解くと、エラーが発生します。
from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))
取得するもの:
raiseNotImplementedError
NotImplementedError
このエラーは、 dsolve()関数を使用した微分方程式系の解が象徴的に表現できないことを意味します。 一方、ラプラス変換の助けを借りて解の象徴的な表現を得たので、これは提案された方法の有効性を証明します。
ご注意
dsolve()関数を使用して微分方程式を解くために必要な方法を見つけるには、 たとえば 、 classify_ode(eq、f(x))を使用する必要があります。
from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)
取得するもの:
Eq(f(x)、C1 * sin(x)+ C2 * cos(x))
(「nth_linear_constant_coeff_homogeneous」、「2nd_power_series_ordinary」)
(「分離可能」、「1st_exact」、「almost_linear」、「1st_power_series」、「lie_group」、「separable_Integral」、「1st_exact_Integral」、「almost_linear_Integral」)
[Eq(f(x)、-acos((C1 + Integral(0、x))* exp(-Integral(-tan(x)、x)))+ 2 * pi)、Eq(f(x)、 acos((C1 +積分(0、x))* exp(-積分(-tan(x)、x)))]]
したがって、方程式eq = Eq(f(x).diff(x、x)+ f(x)、0)の場合、最初のリストの任意のメソッドが機能します。
nth_linear_constant_coeff_homogeneous、
2nd_power_series_ordinary
方程式eq = sin(x)* cos(f(x))+ cos(x)* sin(f(x))* f(x).diff(x)の場合、2番目のリストの任意のメソッドが機能します。
分離可能、1st_exact、almost_linear、
1st_power_series、lie_group、separable_Integral、
1st_exact_Integral、almost_linear_Integral
選択したメソッドを使用するには、dsolve()関数のエントリは次のような形式になります。
rez = dsolve(eq, hint='almost_linear_Integral')
結論:
この記事の目的は、演算子法を使用して線形ODEシステムを解く例で、SciPyおよびNumPyライブラリのツールを使用する方法を示すことです。 したがって、線形微分方程式の記号解法とラプラス法による連立方程式が検討されました。 このメソッドとdsolve()関数で実装されたメソッドのパフォーマンス分析が実行されます。
参照:
- 微分方程式と境界値の問題:Mathematica、Maple、MATLABを使用したモデリングと計算。 第3版。:あたり 英語から -M。:LLC "I.D. ウィリアムズ、2008。-1104 p .:病気。 -パラル。 シジュウカラ。 英語
- 逆ラプラス変換を使用して制御システムの動的リンクを分析する